西安电子科技大学：《大学物理》课程教学讲义（上）20 狭义相对论

狭义相对论 第1节 绝对时空观与伽利略变换 绝对时空观 空间：广延性，“场所”，独立存在，永恒 不变，绝对静止，“容器” 彼此独立 时间：持续性，绝对的、真正的、数学的， 互不相关 “流水”，在永恒地、均匀地流逝着 惯性系 相对量 绝对量 经典力学： 位置坐标 长度，距离，时间 速度 先后次序，时间间隔，同时 二、伽利略变换 m(x,y,z,t) (x',y,z',t) O0重合时，t=t=0 1、事件：某时刻在空间某点上发生的一件事情 2、伽利略变换 t=1 x=x'+ut' x'=x-ut y=y y=y 2=z1 z′=2 1=1' t'=1 3、速度变换 S:v=dr d S:产= d1 d dx dx'udt' V=V:+u ='-u dy dy' V,=V =', dz dz' V.=V' V'=V. dt dt' =+i 产=-元 4、加速度变换 S:a-di ’as a,a= dt 0= dv dt

1 狭义相对论 第 1 节 绝对时空观与伽利略变换 一、绝对时空观 空间：广延性，“场所”，独立存在，永恒 不变，绝对静止，“容器” 彼此独立 时间：持续性，绝对的、真正的、数学的， 互不相关 “流水”，在永恒地、均匀地流逝着 惯性系 相对量 绝对量 经典力学： 位置坐标 长度，距离，时间 速度 先后次序，时间间隔，同时 二、伽利略变换 y y  u m (x, y,z,t) (x  , y  ,z  ,t) S S O O xx  ut x  z （ ut ） z  O O 重合时， t = t = 0 1、事件：某时刻在空间某点上发生的一件事情 2、伽利略变换 t = t x = x  +ut x  = x −ut y = y  y  = y z = z  z  = z t = t t = t 3、速度变换 S ： dt dr V   = ， dt dx Vx = ， dt dy Vy = ， dt dz Vz = S ： dt dr V    =   ， dt dx Vx    = ， dt dy Vy    = ， dt dz Vz    = dx = dx  +udt Vx =Vx  + u Vx  =Vx − u dy = dy  Vy Vy =  Vy =Vy  dz = dz  Vz Vz =  Vz =Vz  dt = dt V V u    =  + V V u     = − 4、加速度变换 S ： dt dV a   = ， dt dV a x x = ， dt dV a y y = ， dt dV a z z =

S”:a=an dv' dh'’ a=d dr, d,= dv dr' dt' dv,=dv" a,=a' a-a dv,dv, a,a, 牛顿力学中 dv.dv. a.=a 加速度是绝对的 dt dt' 三、力学相对性原理 经典力学，质量、力是绝对的 S S' 质点 m m m=m a a-a' 合外力 F , F= F=ma F=ma 牛顿第二定律具有伽利略变换不变性 所有经典力学定律都具有伽利略变换不变性 动量守恒定律S:∑m,=C,S:∑m=C 定律的不变性：定律的数学表达形式不变 力学（伽利略)相对性原理： 在所有惯性系中，力学定律都相同 第2节狭义相对论的两个基本假设 洛仑兹变换 一、经典物理学的困难 绝对参照系 麦克斯韦方程组，不具有伽利略变换不变性 c2-u c+u c2-u 绝对参照系 麦克尔逊莫雷实验 在地球上及在任意一个惯性系中，光沿各个方向的传播 速度都相同，都等于同一个恒量c 二、爱因斯坦的两个基本假设 爱因斯坦：相对性原理应当是普遍适用的 “绝对静止”不符合力学现象及电磁学现象 2

2 S ： dt dV a    =   ， dt dV a x x    = ， dt dV a y y    = ， dt dV a z z    = dVx dVx =  ax ax =  a = a    dVy dVy =  ay ay =  牛顿力学中 dVz dVz =  az az =  加速度是绝对的 dt = dt 三、力学相对性原理 经典力学，质量、力是绝对的 S S 质点 m m  m = m  a  a   a = a    合外力 F  F   F = F   F ma   = F = m  a    牛顿第二定律具有伽利略变换不变性 所有经典力学定律都具有伽利略变换不变性 动量守恒定律 S ： miVi C    = ， S ： mi Vi  = C   定律的不变性：定律的数学表达形式不变 力学（伽利略）相对性原理： 在所有惯性系中，力学定律都相同 第 2 节 狭义相对论的两个基本假设 洛仑兹变换 一、经典物理学的困难 绝对参照系 麦克斯韦方程组，不具有伽利略变换不变性 y y  c 2 2 c −u u S S c O c x c + u O c −u x  c 2 2 c −u 绝对参照系 麦克尔逊-莫雷实验 在地球上及在任意一个惯性系中，光沿各个方向的传播 速度都相同，都等于同一个恒量 c 二、爱因斯坦的两个基本假设 爱因斯坦：相对性原理应当是普遍适用的 “绝对静止”不符合力学现象及电磁学现象

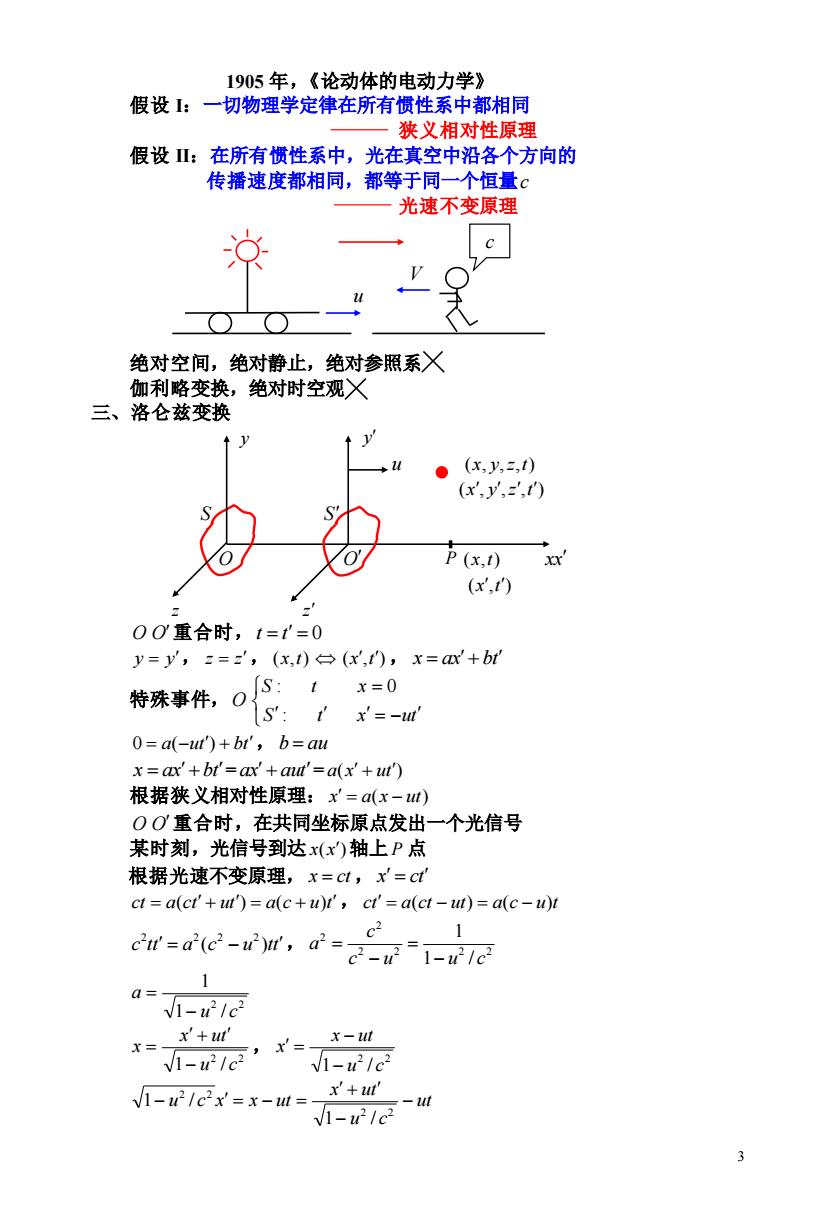
1905年，《论动体的电动力学》 假设：一切物理学定律在所有惯性系中都相同 一 狄义相对性原理 假设Ⅱ：在所有惯性系中，光在真空中沿各个方向的 传播速度都相同，都等于同一个恒量c 光速不变原理 绝对空间，绝对静止，绝对参照系X 伽利略变换，绝对时空观X 三、洛仑兹变换 (x,y,=,t) (x',y,z',t) P(x,t) (x',t) OO重合时，t=t'=0 y=y',='(x,t)(x,t),x=ax'+bt' 特殊事件，oS：1 x=0 Is:t x'=-l 0=a(-ut')+bt',b=au x ax'+bt'=ax'aut'=a(x'+ut') 根据狭义相对性原理：x'=a(x-t) O0重合时，在共同坐标原点发出一个光信号 某时刻，光信号到达x(x)轴上P点 根据光速不变原理，x=ct,x=ct ct a(ct'+ut)=a(c+u)t',ct'=a(ct-ut)=a(c-u)t ow-dlc-w,d- 1 1 a=- 1-21c2 x'+ut' x=- -/c’r=x-w V1-u21c2 V1-2/c2x'=x-t= x′+ut' - V1-u2/c2 3

3 1905 年，《论动体的电动力学》 假设 I：一切物理学定律在所有惯性系中都相同 狭义相对性原理 假设 II：在所有惯性系中，光在真空中沿各个方向的 传播速度都相同，都等于同一个恒量 c 光速不变原理 V u 绝对空间，绝对静止，绝对参照系 伽利略变换，绝对时空观 三、洛仑兹变换 y y  u (x, y,z,t) (x  , y  ,z  ,t) S S O O P (x,t) xx  (x  ,t) z z  O O 重合时， t = t = 0 y = y ， z = z ， (x,t)  (x  ,t) ， x = ax  +bt 特殊事件， O       = −  = S t x ut S t x : : 0 0 = a(−ut) + bt， b = au x = ax  +bt= ax  + aut= a(x  + ut) 根据狭义相对性原理： x  = a(x − ut) O O 重合时，在共同坐标原点发出一个光信号 某时刻，光信号到达 x(x ) 轴上 P 点 根据光速不变原理， x = ct ， x  = ct ct = a(ct + ut) = a(c + u)t， ct = a(ct − ut) = a(c − u)t c tt = a (c − u )tt 2 2 2 2 ， 2 2 2 2 2 2 1 / 1 c u u c c a − = − = 2 2 1 / 1 u c a − = 2 2 1 u / c x ut x −  +  = ， 2 2 1 u / c x ut x − −  = ut u c x ut u c x x ut − −  +  −  = − = 2 2 2 2 1 / 1 / c

a-x=+d--r1ew,1= 1+ C 1-21c 洛仑兹变换： x'+ut' x-ut x=- x'= 1-u2/c2 V1-u2/c2 y=y y'=y 2=z' z′=z t+4 t=- -ulc t'= V1-n2/c2 注意： (1)洛仑兹变换是同一个事件 在两个参照系中时空坐标之间的关系 (2)u<c,u/c2→0,21c20 x≈x+ut,y=y',z=z',t≈t (3)“<c,真空光速是一切物体运动速度的上限 (4)u=0,恒等变换，x=x,y=y,z=z,t=t 例：地面参照系S中，在x=1.0×10m处，于t=0.02s时刻爆炸了 一颗炸弹。一飞船沿x轴正向运动，速率u=0.75c 求：飞船参照系S中的观察者测得炸弹爆炸的地点和时间 解：x= x-W=1.0×105-0.75×3x10'×0.02=-5.29×10m V1-u2/c2 V1-(0.75)2 0.02、0.75 ×1.0×10 t=-㎡1c C 3×108 -=0.0265s V1-(0.75)2 按照伽利略变换 x'=x-ut=-3.5×10°m t'=t=0.02s 4

4 x x ut u c ut c u 2 2 2 2 (1− )  =  +  − 1− / ， 2 2 2 1 u / c x c u t t −  +  = 洛仑兹变换： 2 2 1 u / c x ut x −  +  = 2 2 1 u / c x ut x − −  = y = y  y  = y z = z  z  = z 2 2 2 1 u / c x c u t t −  +  = 2 2 2 1 u / c x c u t t − −  = 注意： （1）洛仑兹变换是同一个事件 在两个参照系中时空坐标之间的关系 （2） u c， / 0 u c 2 → ， / 0 u 2 c 2 → x  x  +ut ， y = y ， z = z ， t  t （3） u  c ，真空光速是一切物体运动速度的上限 （4） u = 0 ，恒等变换， x = x ， y = y ， z = z ，t = t 例：地面参照系 S 中，在 x m 6 =1.010 处，于 t = 0.02s 时刻爆炸了 一颗炸弹。一飞船沿 x 轴正向运动，速率 u = 0.75c 求：飞船参照系 S 中的观察者测得炸弹爆炸的地点和时间 解： 2 2 1 u / c x ut x − −  = = m 6 2 6 8 5.29 10 1 (0.75) 1.0 10 0.75 3 10 0.02 = −  −  −    2 2 2 1 u / c x c u t t − −  = = 0.0265s 1 (0.75) 1.0 10 3 10 0.75 0.02 2 6 8 = −    − 按照伽利略变换 x x ut m 6  = − = −3.510 t = t = 0.02s