
§4.5多电子原子的原子态和能级 价电子间的相互作用 ·除了前述静电相互作用之外 ·由于两个电子各自都有轨道运动和自旋运动,如果分别表 示为/1,12,s1,s2,由于其中任何两种运动间都会引起 磁相互作用,则它们之间的相互作用共有以下几种: ·1、两个电子自旋运动之间的相互作用 ·2、两个电子轨道运动之间的相互作用 ·3、同一个自旋—轨道运动之间的相互作用 ·4、一个电子的自旋运动和另一个电子的轨道运动之间的 相互作用
§4.5 多电子原子的原子态和能级 价电子间的相互作用 • 除了前述静电相互作用之外 • 由于两个电子各自都有轨道运动和自旋运动,如果分别表 示为l1,l2,s1,s2,由于其中任何两种运动间都会引起 磁相互作用,则它们之间的相互作用共有以下几种: • 1、两个电子自旋运动之间的相互作用 • 2、两个电子轨道运动之间的相互作用 • 3、同一个自旋—轨道运动之间的相互作用 • 4、一个电子的自旋运动和另一个电子的轨道运动之间的 相互作用

用量子数表示为 G1(S1,S2) G2(1,12) G3(4,S) G4(L2,S2) G(4,S2) G6(L2,S1) ·两个电子间的自旋一 轨道相互作用弱得 多,可以忽略 对于其余的相互作用,可以分别不同的情 况进行处理 ·采用耦合的方法处理
用量子数表示为 • 两个电子间的自旋——轨道相互作用弱得 多,可以忽略 • 对于其余的相互作用,可以分别不同的情 况进行处理 • 采用耦合的方法处理 1 1 2 G s s ( , ) 2 1 2 G l l ( , ) 3 1 1 G l s ( , ) 4 2 2 G l s ( , ) 5 1 2 Gls ( , ) 6 2 1 G l s ( , )

1、LS耦合 G1(S1,S2),G2(1,l2)>>G3(1,S),G4(L2,S2)) 。 两个电子间的自旋作用较强,两个电子间的 轨道作用也较强 则两个电子的自旋运动要合成为一个总的自 旋运动 则两个电子的轨道运动也要合成为一个总的 轨道运动 总的自旋角动量与总的轨道角动量再合成为 一个总的角动量
1、LS耦合 • 两个电子间的自旋作用较强,两个电子间的 轨道作用也较强 • 则两个电子的自旋运动要合成为一个总的自 旋运动 • 则两个电子的轨道运动也要合成为一个总的 轨道运动 • 总的自旋角动量与总的轨道角动量再合成为 一个总的角动量 1 1 2 2 1 2 3 1 1 4 2 2 G s s G l l G l s G l s ( , ), ( , ) ( , ), ( , )
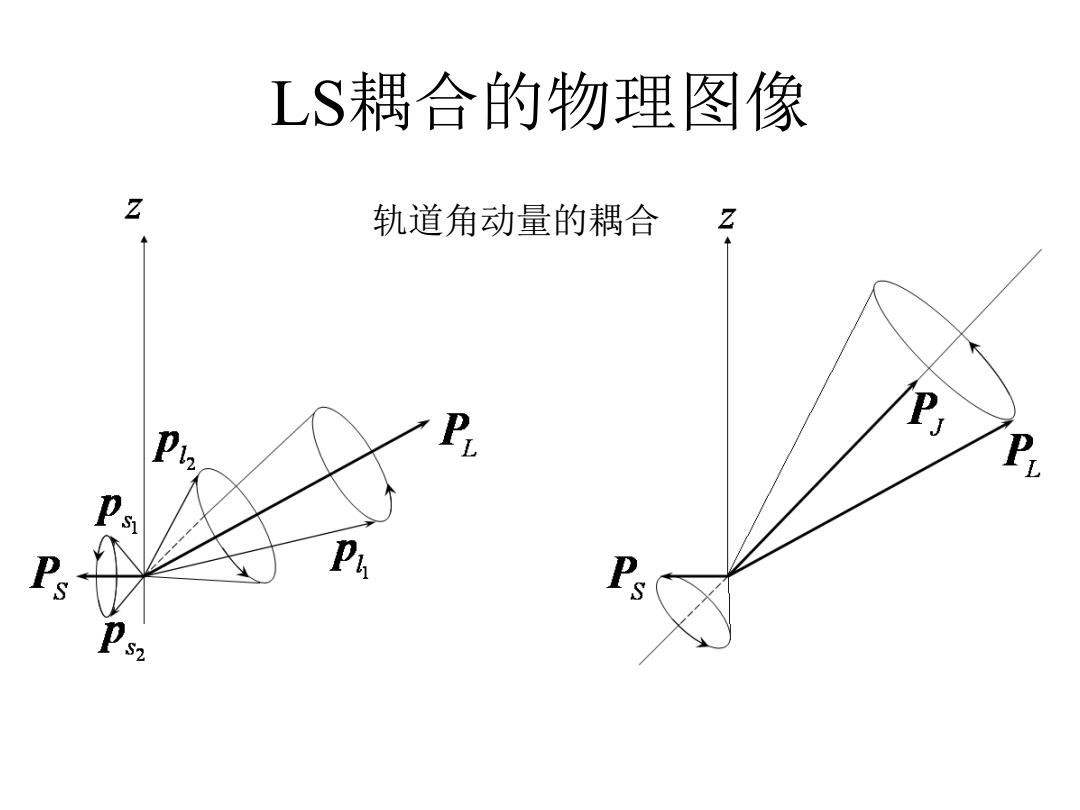
LS耦合的物理图像 Z 轨道角动量的耦合 Z P S P D
LS耦合的物理图像 轨道角动量的耦合

i+i=,L=1+12,4+12-1,…4-12 L=L(L+1)h he mnh 12.=m2h L.=mh m,=m1+2=-(+l2)2…,0,…,4+12
1 2 l l L 1 1 z l l m 2 2 z l l m L m z l m m m l l l 1 2 1 2 1 2 ( ), ,0, , l l l l 1 2 1 2 1 2 L l l l l l l , -1 | , | L L L ( 1)

设l1>2,则m1=1、m1=-11的11与各个取向 的2合成的结果,相当于得到一个总的轨道 角动量, 其m=l1+12,1+2-1, (11+l2),即L=l1+l2。 依此原则,每一对角动量的合成,都 可以得到一个总的轨道角动量。所以, 最后,可能的总轨道角动量的量子数 为L=1+l2,1+12-1,...L=1-l2。共 有212十1个。 1+i= :L=VL(L+)方 L=1+12,1+12-1,…4-12
设l1>l2,则ml1=l1、 ml1=-l1的l1与各个取向 的l2合成的结果,相当于得到一个总的轨道 角动量, 其mL=l1+l2,l1+l2-1,……, -(l1+l2),即L=l1+l2。 依此原则,每一对角动量的合成,都 可以得到一个总的轨道角动量。所以, 最后,可能的总轨道角动量的量子数 为 L=l1+l2,l1+l2-1,…… L=l1-l2。共 有2l2+1个。 1 2 l l L 1 2 1 2 1 2 L l l l l l l , -1 | , | L L L ( 1)

最后,L和S耦合得到原子的总角动量J 5+i=j 总角动量值J=V√J(J+1)h 量子数 J=L+S,L+S-1,…,L-S 耦合后所形成的原子态 n2s+L
S L J J L S L S L S , 1 | , ,| J J J ( 1) S J L 耦合后所形成的原子态 2 1L s J n 最后,L和S耦合得到原子的总角动量J 量子数 总角动量值

例1:电子组态2p3d所形成的原子态 n=21=1S=1/2n2=31=2S2=1/2 LS耦合 S=S1+S2=1,0 L=1+12=3,2,1 每一个L和每一个S都形成一个J 共有12种原子组态,即运动状态,可以列表表示为 S S=0 S=1 S=0 S=1 L=1 1 2,1,0 L=1 P 3P20 L=2 2 3,2,1 L=2 1D2 3D321 L=3 3 4,3,2 L=3 F 3F432 单重态 三重态
例1:电子组态2p3d所形成的原子态 S=0 S=1 L=1 1 2,1,0 L=2 2 3,2,1 L=3 3 4,3,2 1 l 1 2 l 2 1 s 1/ 2 2 s 1/ 2 1 2 S s s 1,0 1 2 L l l 3,2,1 每一个L和每一个S都形成一个J 共有12种原子组态,即运动状态,可以列表表示为 J S L 1 P1 3 P210 1 D2 1 F3 3 D321 3 F432 S=0 S=1 L=1 L=2 L=3 1 n 2 2 n 3 LS耦合 单重态 三重态

耦合所形成的能级 F 单重态 pd ①2 P 倒转次序 3 P; 2 D 正常次序 三重态 ①4 3 正常次序
耦合所形成的能级 pd 1 P1 1 D2 1 F3 3 P1 3 P2 3 P0 3 F3 3 F2 3 F4 3 D2 3 D3 3 D1 单重态 三重态 正 常 次 序 正 常 次 序 倒 转 次 序 3 3 2 2 1 4

Lande间隔定则 在多重态中,一对相邻的能级之间的间隔 与有关的两个J之中较大的那个值成正比 在LS耦合下,自旋一轨道相互作用所引起 的附加能量为 U。=5(L,S)L·S=55(L,S)(J2-L2-S2) ·所引起的能级移动为 E,=25(L,S[JW+)-(L+)-(S+10S] ·相邻能级间隔 E,-E,=25L,S[W+2+1)-JW+1】=5(L,SMW+10
Landè间隔定则 • 在多重态中,一对相邻的能级之间的间隔 与有关的两个J之中较大的那个值成正比 • 在LS耦合下,自旋-轨道相互作用所引起 的附加能量为 • 所引起的能级移动为 • 相邻能级间隔 ( , )( ) 2 1 ( , ) 2 2 2 Us o L S L S L S J L S 1 ( , )[ ( 1) - ( 1) -( 1) ] 2 E L S J J L L S S J 1 1 ( , )[( 2)( 1) - ( 1)] 2 E E L S J J J J J J ( , )( 1) L S J