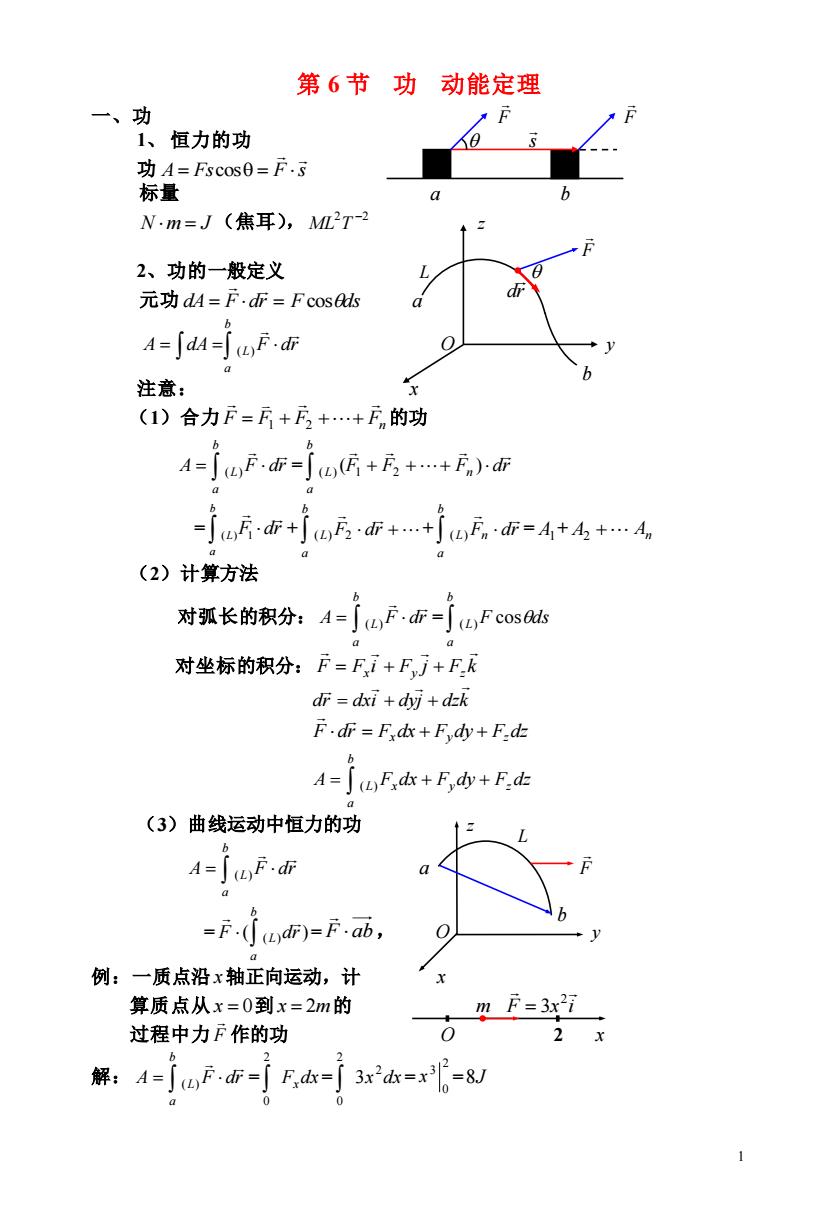
第6节功动能定理 一、功 1、恒力的功 功A=Fs cos0=F.S 标量 Nm=J(焦耳),ML2T-2 2、功的一般定义 元功dA=F.f=Fcos A-∫dA=uF.i 注意: (1)合力F=++…+Fn的功 A=juF.=ju+店++f) =ju市+小o店面++f瓦n=4+4+…4, (2)计算方法 对弧长的积分:A-jF=s 对坐标的积分:F=Fi+Fj+FR dr dxi +dyj +dzk F.dr=Fdx +Fdy+F.dz A=∫Fdk+F,w+F.d止 (3)曲线运动中恒力的功 A=∫F.i -F.(Jdr)-F.ab, 例:一质点沿x轴正向运动,计 算质点从x=0到x=2m的 m F=3x2i 过程中力F作的功 解:4=aF---了3=6=8
1 第 6 节 功 动能定理 一、功 F F 1、 恒力的功 s 功 A Fs F s = cos = 标量 a b N m = J (焦耳), 2 −2 ML T z F 2、功的一般定义 L 元功 dA = F dr = F cosds a A dA F dr b a L = = ( ) O y 注意: x (1)合力 F F F Fn = 1 + 2 + + 的功 A F dr b a L = ( ) = F F F dr n b a L + + + ( ) ( ) 1 2 = F dr b a L ( ) 1 + + F dr b a (L) 2 + F dr n b a L ( ) = A1 + A2 + An (2)计算方法 对弧长的积分: A F dr b a L = ( ) = F ds b a (L) cos 对坐标的积分: F F i F j F k x y z = + + dr dxi dyj dzk = + + F dr F dx F dy F dz = x + y + z A = F dx F dy F dz x y z b a L + + ( ) (3)曲线运动中恒力的功 z A F dr b a L = ( ) a F = ( ) ( ) F dr b a L = F ab , O y 例:一质点沿 x 轴正向运动,计 x 算质点从 x = 0 到 x = 2m 的 m F x i 2 = 3 过程中力 F 作的功 O 2 x 解: A F dr b a L = ( ) = F dx x 2 0 = x dx 2 2 0 3 = 2 0 3 x =8J dr b L b

例:计算质点从a到b移动 半个圆周的过程中摩 擦力的功,设质点与桌 面的摩擦系数μ为常数 解:摩擦力的大小∫=g 方向与而反方向 A=j了.df=∫fcos@ds=∫umg-l)dk=-mgR (1)子是不是恒力? (不是,不能用子·ab计算功) (2)如果质点沿直径从a到b,摩擦力的功是多少? (A=-umg2R) 3、功率 P=近 dt dA=F.dr 功率P=d4 dt 标量,Js1=W(瓦),MLT3 p-dA-F.dF-F.V-FVcos0 dtdt 如果F1,则P=0 二、几种常见力的功 1、重力的功 F=-mgk x,,) L m -2 A-SF.d=Ed, ↓1mg b(x2,y2,22) mgdz=-mg(21), X 特点: (1)、与质点走过的路径无关 (2)、质点下降,重力作正功:质点上升,重力作负功 2
2 例:计算质点从 a 到 b 移动 半个圆周的过程中摩 擦力的功,设质点与桌 面的摩擦系数 为常数 O 解:摩擦力的大小 f = mg 方向与 dr 反方向 A f dr b a L = ( ) = f ds b a (L) cos = mg ds b a L ( 1) ( ) − = − mgR (1) f 是不是恒力? (不是,不能用 f ab 计算功) (2)如果质点沿直径从 a 到 b ,摩擦力的功是多少? ( A = −mg2R ) 3、功率 dt dr V = dt dr dA F dr = F 功率 P = dt dA 标量, Js =W −1 (瓦), 2 −3 ML T P = dt dA = dt F dr = F V = FV cos 如果 F V ⊥ ,则 P =0 二、几种常见力的功 1、 重力的功 z F mgk = − ( , , ) 1 1 1 a x y z L m A F dr b a L = ( ) = F dz z z z 2 1 , g mg ( , , ) 2 2 2 b x y z = mgdz z z − 2 1 = ( ) 2 1 − mg z − z , x 特点: (1)、与质点走过的路径无关 (2)、质点下降,重力作正功;质点上升,重力作负功 b R f dr m O y μ a

2、万有引力的功 F=G 2 F=-GmM.F r2 r 4-juF r b d(A.B)=dA.B+A.dBB d(A·A=d☑A+AdA=2AdA A.A=-= d(A.A)=2AdA A.dA=AdA 令A=r,Fdf=rd 4=f-Gm4。 GmM=GmMl-马 r ra 特点: (1)、与质点走过的路径无关 (2)、质点m由远及近靠近M,万有引力作正功 质点m由近及远远离M,万有引力作负功 3、弹力的功 F=-kxi m F=-kx F=-kx ●●●】 x bx A=jwF-了F=了-k=-(-) 特点: (1)、与质点走过的路径无关 (2)、形变量:减小,弹力作正功 形变量增加,弹力作负功 4、摩擦力的功 特点: 不仅与质点的始末位置有关,还与质点走过的路径有关 3
3 2、 万有引力的功 2 r mM F = G a L r r r mM F G = − 2 a r r m A F dr b a L = ( ) M = dr r r r mM G b a L − ( ) 2 d A B dA B A dB ( ) = + 令 A B = d A A dA A A dA A dA ( ) = + = 2 2 2 2 A A = A = A = A d(A A) = 2AdA A dA = AdA 令 A r = , r dr = rdr A = − b a r r dr r mM G 2 = a b r r r GmM = ) 1 1 ( b a r r GmM − 特点: (1)、与质点走过的路径无关 (2)、质点 m 由远及近靠近 M ,万有引力作正功 质点 m 由近及远远离 M ,万有引力作负功 3、 弹力的功 F kxi = − k m F = −kx F = −kx O a x b x A F dr b a L = ( ) = b a x x Fdx = − b a x x kxdx= ( ) 2 1 2 2 b a − k x − x 特点: (1)、与质点走过的路径无关 (2)、形变量 x 减小,弹力作正功 形变量 x 增加,弹力作负功 4、 摩擦力的功 特点: 不仅与质点的始末位置有关,还与质点走过的路径有关 F b b r

三、动能定理 1、质点的动能定理 dA=F.dr=ma.d=m .d, dt =mv.dv=mVdv=d(mv2) 、F合外力 定义:质点的动能E=二mV2 dEk=dA— 质点动能定理(微分形式) △Ek=A— 质点动能定理(积分形式) 2、质点系和质点系的动能定理 由n(22)个质点构成的系统 称为质点系,内力,外力 Jy+F=0, 方=∑:m,受到的合内力月 善:质点系的所有内力之和, -立0 m,:合外力E,合内力,合力E+,d,位移而 d(与m的)=(匠+》面=月面+万,i=12n 三m)2成+空i成 d∑2m?=∑E面+∑7面 ∑E·d而=dA外,∑j·而=dA内 定义:质点系动能E=∑)m dE=dA外+d4内:质点系动能定理(微分形式) △E:=A外+A内:质点系动能定理(积分形式) 说明:(1)、只适用于惯性系 (2)、 ∑,=0,∑j而≠0 (3)、单个质点:合力的功=每个力作功的代数和 质点系:合力的功没有意义,只能先计算每个力的功 然后对功求和 4
4 三、动能定理 1、 质点的动能定理 dA F dr = = ma dr = Vdt dt dV m , dr L = mV dV = mVdV = ) 2 1 ( 2 d mV , F 合外力 定义:质点的动能 2 2 1 Ek = mV dEk = dA 质点动能定理(微分形式) Ek = A 质点动能定理(积分形式) 2、 质点系和质点系的动能定理 由 n( 2) 个质点构成的系统 称为质点系,内力,外力 ij f + ji f =0, mi mj = = n j j i i ij f f 1, : mi 受到的合内力 = n i i f 1 :质点系的所有内力之和, = = = = n j j i ij n i n i i f f 1 1 1, =0 mi :合外力 Fi ,合内力 i f ,合力 Fi + i f ,dt ,位移 i dr i i i i i i i i i d mV F f dr F dr f dr ) = ( + ) = + 2 1 ( 2 , i = 1,2, n = = = = + n i i i n i i i n i i i d m V F dr f dr 1 1 1 2 ) 2 1 ( = + i i i i i i d m V F dr f dr 2 2 1 外 Fi dri = dA , = 内 f i dri dA 定义:质点系动能 = 2 2 1 Ek miVi 外 内 dEk = dA + dA :质点系动能定理(微分形式) 外 内 Ek = A + A :质点系动能定理(积分形式) 说明:(1)、只适用于惯性系 (2)、 0 1 = = n i i f , f i dri 0 (3)、单个质点:合力的功=每个力作功的代数和 质点系:合力的功没有意义,只能先计算每个力的功 然后对功求和 ij f ji f m
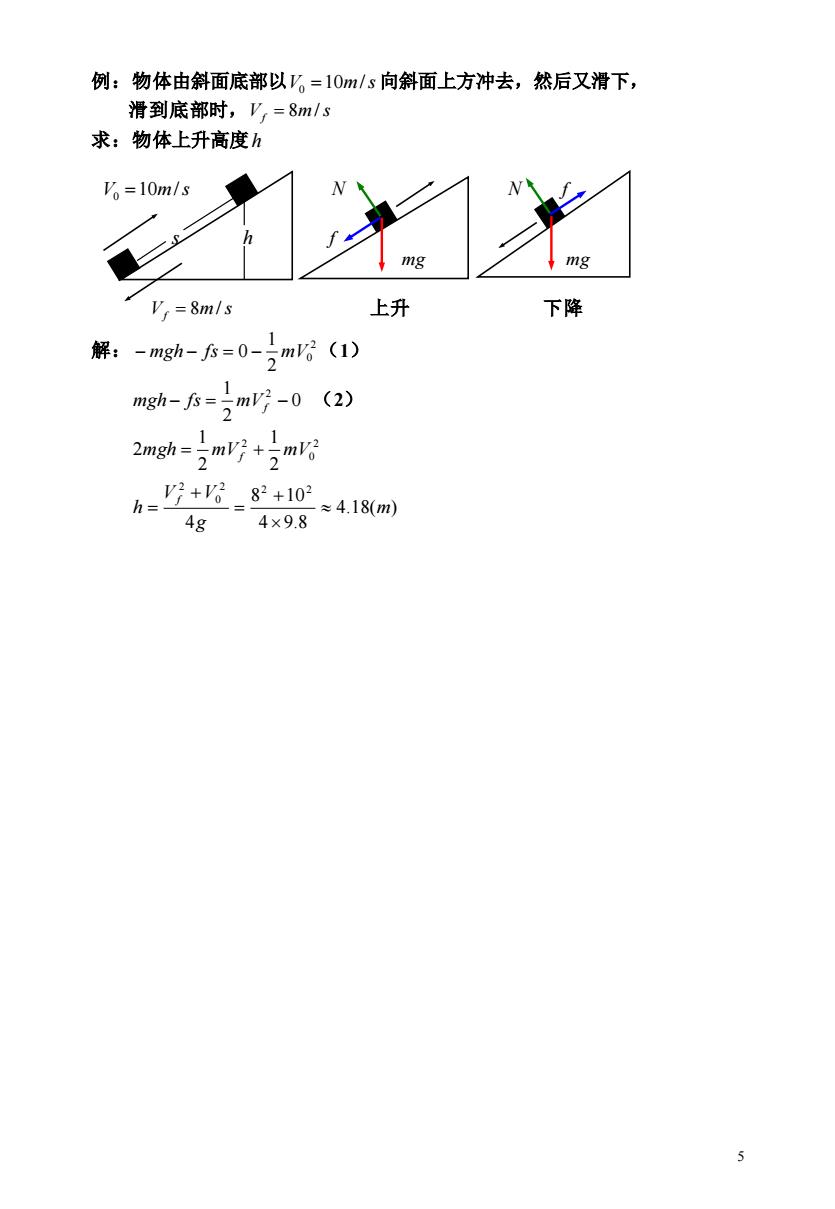
例:物体由斜面底部以。=l0m/s向斜面上方冲去,然后又滑下, 滑到底部时,V,=8m/s 求:物体上升高度h 'o=10m/s mg mg Vr=8mls 上升 下降 解,-mgh-店=0-m(1) meh-=m吗-0(a) 2ngh=5nV2+。m3 "2 咛+682+102 ≈4.18(m) 4g 4×9.8
5 例:物体由斜面底部以 V 10m/s 0 = 向斜面上方冲去,然后又滑下, 滑到底部时, V m s f = 8 / 求:物体上升高度 h V 10m/s 0 = N N f s h f mg mg V m s f = 8 / 上升 下降 解: 2 0 2 1 − mgh − fs = 0 − mV (1) 0 2 1 2 mgh − fs = mVf − (2) 2 0 2 2 1 2 1 2mgh = mVf + mV 4.18( ) 4 9.8 8 10 4 2 2 2 0 2 m g V V h f + = + =