质点和质点系动力学习题课 例:以初速度',平抛一小球m,小球与地面发生完全弹性碰撞后 又恢复到原来高度,整个过程中那些物理量守恒? mg mg 答:机械能守恒,动量不守恒,但动量的x分量守恒 例:船1=4m,M=150kg,人m=50kg 人由船的一端走到另一端 求:人、船相对岸边走过 M 的距离 (不计水的阻力) 解:水平方向动量守恒 设人对岸边的速率y 船对岸边的速率V MV-mv =0,MV=mv M[Vdt=mvdt,S=Vdt,s=[vdt MS=ms,S+s=1,S=1-s M0-)=mss=M-3m,S=1-9=l(m》 M+m 例:质量M的平板车,在水平面上无摩擦运动,有N个人,质量 均为m,站在车上。开始,车以。向右运动,后来,人相对车 以向左跑 u, m N个 M 求证:(1)N个人同时跳离车后,车速V='。+ Nmu M+Nm (2)N个人相继离车后,车速 mu mu mu W='%+ M+Nm M+(N-1)m M+m U, ○m○ N个() M 证明:(1)设同时跳车后,车速为V 1
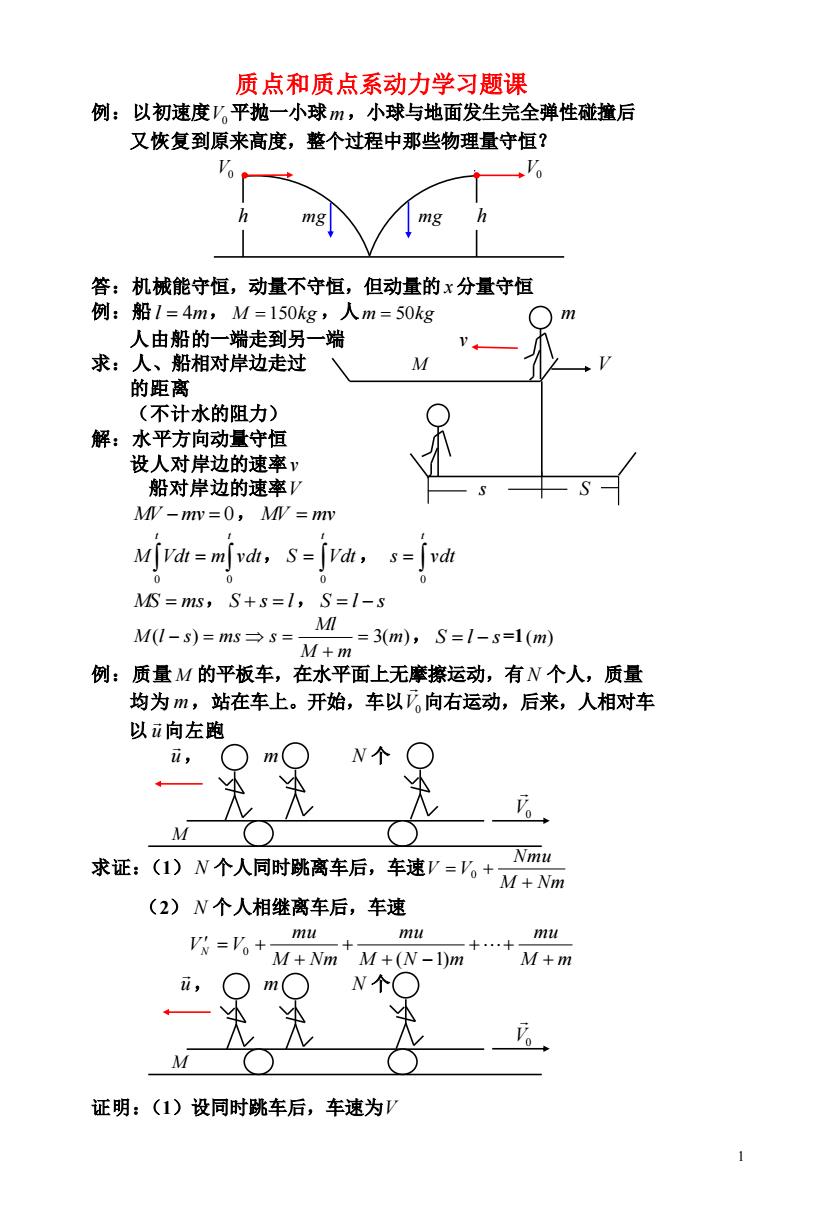
1 质点和质点系动力学习题课 例:以初速度 V0 平抛一小球 m ,小球与地面发生完全弹性碰撞后 又恢复到原来高度,整个过程中那些物理量守恒? V0 V0 h mg mg h 答:机械能守恒,动量不守恒,但动量的 x 分量守恒 例:船 l = 4m, M = 150kg ,人 m = 50kg m 人由船的一端走到另一端 v 求:人、船相对岸边走过 M V 的距离 (不计水的阻力) 解:水平方向动量守恒 设人对岸边的速率 v 船对岸边的速率 V s S MV −mv = 0, MV = mv = t t M Vdt m vdt 0 0 , = t S Vdt 0 , = t s vdt 0 MS = ms, S + s = l, S = l − s ( ) 3(m) M m Ml M l s ms s = + − = = , S = l − s =1 (m) 例:质量 M 的平板车,在水平面上无摩擦运动,有 N 个人,质量 均为 m ,站在车上。开始,车以 V0 向右运动,后来,人相对车 以 u 向左跑 u , m N 个 V0 M 求证:(1) N 个人同时跳离车后,车速 M Nm Nmu V V + = 0 + (2) N 个人相继离车后,车速 M m mu M N m mu M Nm mu VN V + + + + − + + = + ( 1) 0 u , m N 个 V0 M 证明:(1)设同时跳车后,车速为 V

(M+Nm)v=MV Nm(-u+V) V=V。+M+Nm Nmu (2)设第一个人跳车后,车速为以 (M+Nm)'o=[M+(N-1)m''+m(-u+) 以=%+、mu M+Nm 第二个人跳车后,设车速为 [M+(N-1)mY'=[M+(N-2)m]g+m(-u+ 以=+, mu =+ mu mu M+(N-1)m M+Nm M+(N-1)m 54555 第N个人跳车后,设车速为W mu mu mu VN=Vo+- 十十 M+Nm M+(N-1)m M+m 例:m,m2,1,相互作用 符合万有引力定律 1m3 求:两质点间距变为12时 V ● 两质点的速度 m1/2 m 解:m-m2'2=0 -Gm座=m2+m,好-G"m% 2 1/2 2G 2G V=m2(m+m) '2=m V(m1+m2)1 例:在两个质点组成的系统中,若质点之间只有万有引力作用, 且此系统所受外力的矢量和为零,则此系统 (A)动量与机械能一定都守恒 (B)动量与机械能一定都不守恒 (C)动量不一定守恒,机械能一定守恒 (D)动量一定守恒,机械能不一定守恒 例:恒力F,m,自平衡位置 由静止开始运动 B F 求:AB系统受合外力为零时的 m 速度,以及此过程中AF、A, 解:AB系统受水平方向合外力 F-kx=0=x=F/k Ap=Fx=F2/k 4,=m+mr+,v= 2 k(m1+m2) 2
2 ( ) ( ) M + Nm V0 = MV + Nm −u +V M Nm Nmu V V + = 0 + (2)设第一个人跳车后,车速为 V1 ( ) [ ( 1) ] ( ) M Nm V0 M N m V1 m u V1 + = + − + − + M Nm mu V V + 1 = 0 + 第二个人跳车后,设车速为 V2 [ ( 1) ] [ ( 2) ] ( ) M N m V1 M N m V2 m u V2 + − = + − + − + = + − = + M N m mu V V ( 1) 2 1 M N m mu M Nm mu V ( 1) 0 + − + + + 第 N 个人跳车后,设车速为 VN M m mu M N m mu M Nm mu VN V + + + + − + + = + ( 1) 0 例: m1, m2,l ,相互作用 符合万有引力定律 m1, l m2 求:两质点间距变为 l /2 时 V1 V2 两质点的速度 m1 l / 2 m2 解: m1V1 − m2V2 = 0 2 / 2 1 2 1 2 1 2 2 2 2 1 1 1 2 l m m m V m V G l m m − G = + − m m l G V m ( ) 2 1 2 1 2 + = , m m l G V m ( ) 2 1 2 2 1 + = 例:在两个质点组成的系统中,若质点之间只有万有引力作用, 且此系统所受外力的矢量和为零,则此系统 (A)动量与机械能一定都守恒 (B)动量与机械能一定都不守恒 (C)动量不一定守恒,机械能一定守恒 (D)动量一定守恒,机械能不一定守恒 例:恒力 F , m1 自平衡位置 由静止开始运动 k A T B F 求:AB 系统受合外力为零时的 m1 m2 速度,以及此过程中 AF 、 AT 解: A B 系统受水平方向合外力 F − kx = 0 x = F / k A Fx F k F / 2 = = 2 2 1 2 2 1 ( ) 2 1 A m m V kx F = + + , ( ) m1 m2 k F V + =
4=m+52=2m+m 2k m+m2 例:三艘船(M)鱼贯而行,速度都是V,从中间船上同时以 相对船的速度把质量都为m的物体分别抛到前后两艘船上 umm1 *1 M 、M 求:抛掷物体后,三艘船的速度? 解:以第二艘船和抛出的两个物体为系统,水平方向动量守恒 (M+2mv=MV,+m(u+v,)+m(-u+v,)=V,=V 以第一船和抛来物体为系统 MW+mu+门=(m+M0y,=V+, mu M+m 以第三船和抛来物体为系统 MW+m-u+)=(m+M)y3,,=V-,m M+m 例:小球(m)从高出弹簧上端h处落下 求:弹簧被压缩的最大距离? 解: mg(h+x)=1kx ) mg x= m)y2+2m8 例:根据质点动量定理推导 两个质点组成的质点系 的动量定理并导出动量, 守恒条件 解:d=(E+f)dt d=(E2+2)dh d(P+P)=(F+F)dt+(+f)dt 万+万2=0 dp=Fd,△=∫Fd 当F=0,P=+P,=C动量守恒 2
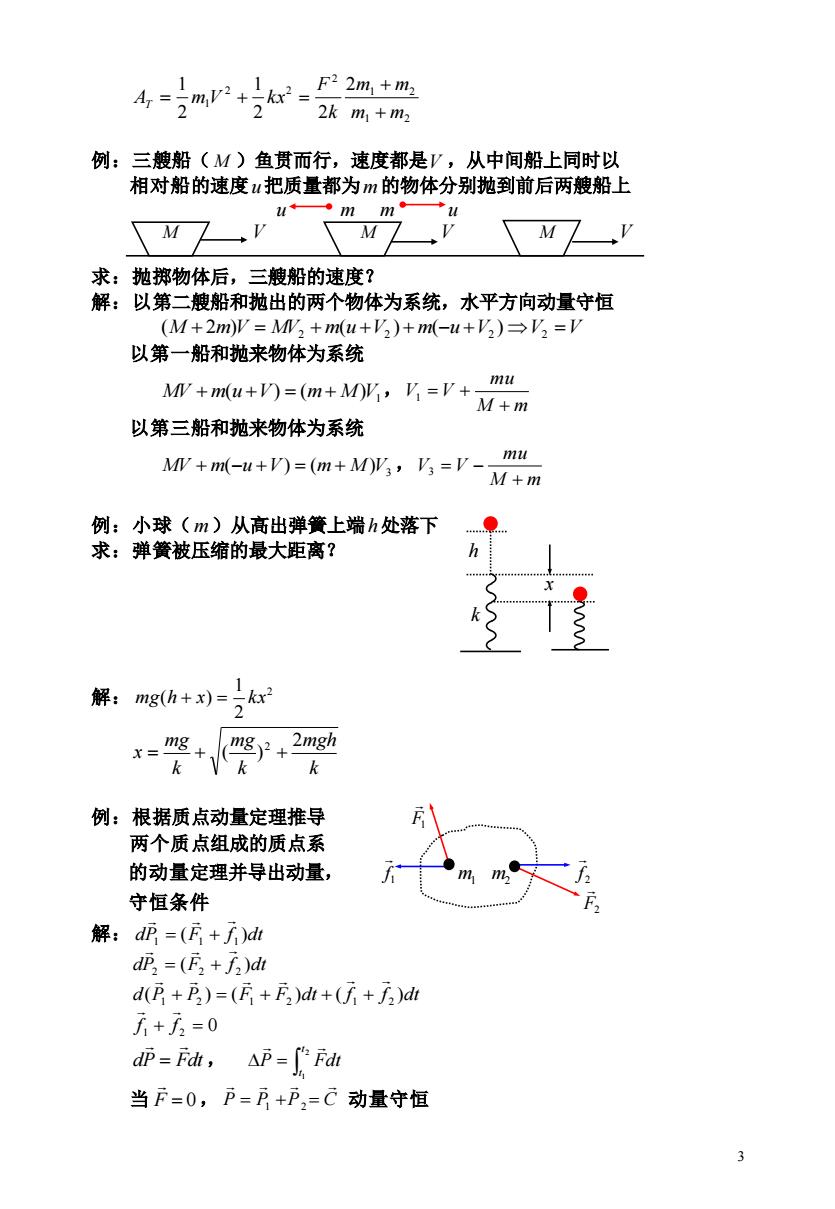
3 AT = 1 2 1 2 2 2 2 1 2 2 2 1 2 1 m m m m k F m V kx + + + = 例:三艘船( M )鱼贯而行,速度都是 V ,从中间船上同时以 相对船的速度 u 把质量都为 m 的物体分别抛到前后两艘船上 u m m u M V M V M V 求:抛掷物体后,三艘船的速度? 解:以第二艘船和抛出的两个物体为系统,水平方向动量守恒 (M + 2m)V = MV2 + m(u +V2 ) + m(−u +V2 ) V2 =V 以第一船和抛来物体为系统 1 MV + m(u +V) = (m+ M)V , M m mu V V + 1 = + 以第三船和抛来物体为系统 3 MV + m(−u +V) = (m + M)V , M m mu V V + 3 = − 例:小球( m )从高出弹簧上端 h 处落下 求:弹簧被压缩的最大距离? h 解: 2 2 1 mg(h + x) = kx k mgh k mg k mg x 2 ( ) 2 = + + 例:根据质点动量定理推导 F1 两个质点组成的质点系 的动量定理并导出动量, 1 f m1 m2 2 f 守恒条件 F2 解: dP (F f )dt 1 1 1 = + dP (F f )dt 2 2 2 = + d(P P ) (F F )dt ( f f )dt 1 2 1 2 1 2 + = + + + f 1 + f 2 = 0 dP Fdt = , = 2 1 t t P Fdt 当 F = 0 , P P P C = 1 + 2= 动量守恒 k x
例 V=700m/s 木板 木板 解:-s=m-m,-=m-n V3=100ms- 例:子弹射中A后嵌入其中 m/2,Vm/2 m 求:(1)V=?VB=? A B (2)Vams = 解:(1)子弹射中A后 子弹与A组成的系统动量守恒 mr=m+mj,-5,,=0 1 (2)V=V/2,ma=mg,Vams =V/2 例:光滑水平面上放一小车 车上放一木箱,恒力F 将木箱从小车一端拉致 另一端,第一次小车固 定,第二次小车不固定, (1)两次F作功相同 (2)两次摩擦力对木箱作功相同 (3)两次木箱获得动能相同 (4)两次因摩擦产生热相同 解:(1)第一次F作功F,第二次F作功F(I+s) (2)第一次f对箱子作功-,第二次-f1+s) (3)第一次合力对箱子作功(F-f)1,第二次(F-fI+s) (4)第一次f的总功-I,第二次-f(I+s)+=- 例:容器自O点(平衡位置)左端1处 从静止开始运动,每经过一次O点 从上方滴入一质量为m的油滴 7 求:(1)滴到容器n滴后,容器 m 运动到O点的最远距离 (2)第n+1滴与第n滴的时间 M☑☑7 间隔 —1.0 解:(1)从开始到O点,机械能守恒 桃=M 2 每次经过O点,动量数值不变 MV =(M+nm)V' 4
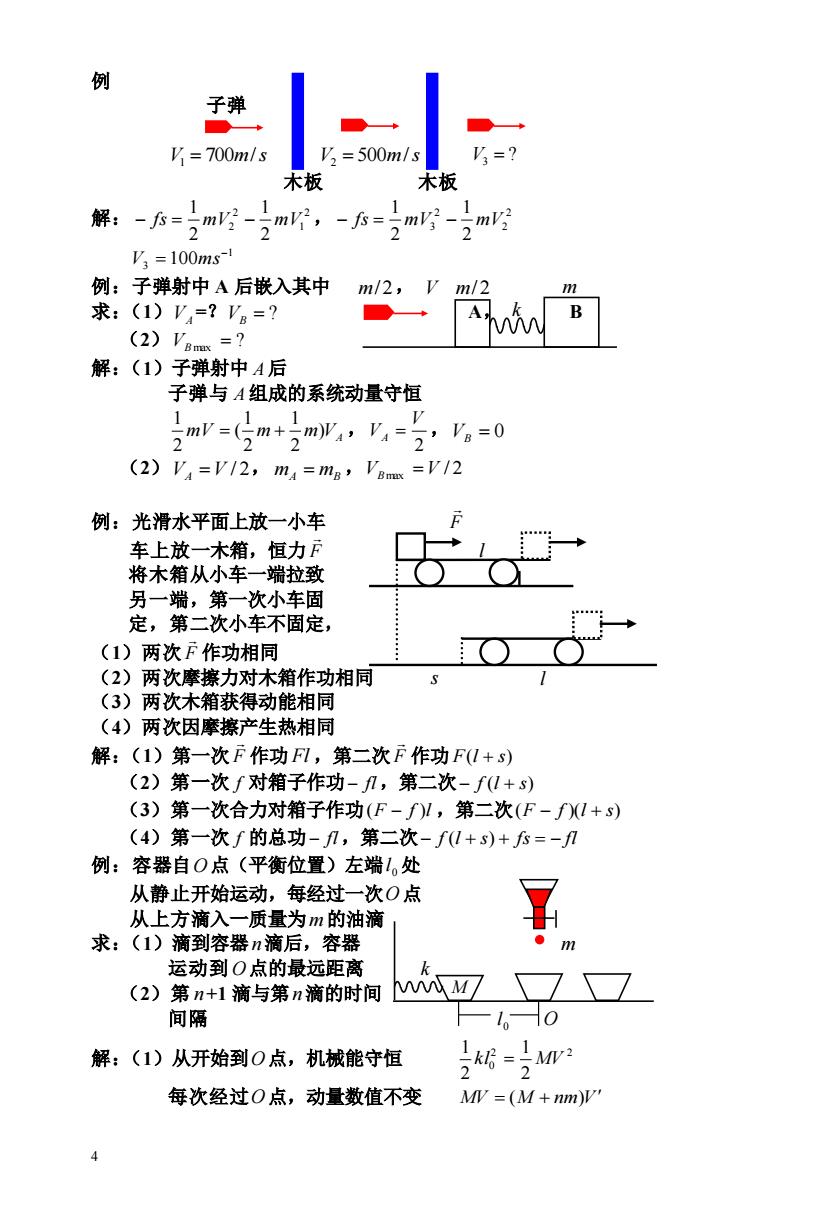
4 例 子弹 V 700m/s 1 = V 500m/s 2 = ? V3 = 木板 木板 解: 2 1 2 2 2 1 2 1 − fs = mV − mV , 2 2 2 3 2 1 2 1 − fs = mV − mV 1 3 100 − V = ms 例:子弹射中 A 后嵌入其中 m/2, V m/2 m 求:(1) VA =? = ? VB A, B (2) ? VB max = 解:(1)子弹射中 A 后 子弹与 A 组成的系统动量守恒 mV m m VA ) 2 1 2 1 ( 2 1 = + , 2 V VA = ,VB = 0 (2) VA =V / 2, mA = mB ,VBmax =V / 2 例:光滑水平面上放一小车 F 车上放一木箱,恒力 F l 将木箱从小车一端拉致 另一端,第一次小车固 定,第二次小车不固定, (1)两次 F 作功相同 (2)两次摩擦力对木箱作功相同 s l (3)两次木箱获得动能相同 (4)两次因摩擦产生热相同 解:(1)第一次 F 作功 Fl ,第二次 F 作功 F(l + s) (2)第一次 f 对箱子作功− fl ,第二次− f (l + s) (3)第一次合力对箱子作功 (F − f )l ,第二次 (F − f )(l + s) (4)第一次 f 的总功− fl ,第二次− f (l + s) + fs = − fl 例:容器自 O 点(平衡位置)左端 0 l 处 从静止开始运动,每经过一次 O 点 从上方滴入一质量为 m 的油滴 求:(1)滴到容器 n 滴后,容器 m 运动到 O 点的最远距离 k (2)第 n +1 滴与第 n 滴的时间 间隔 0 l O 解:(1)从开始到 O 点,机械能守恒 2 2 0 2 1 2 1 kl = MV 每次经过 O 点,动量数值不变 MV = (M + nm)V M k
滴入n滴后到最远更离机械能守恒山+m”:=女 x=M/(M+nm).lo (2)1n1-tn=亏Tn=πV(M+m)/k 例:链条m=10kg,1=40cm m 1=l2=20cm<l3,m=10kg 求:链条全部滑到桌面时 系统的速度及加速度 m mg 11,1 解:m8=m8+立m+mr 2 m1=m,1=1/2 3 V=V8=1.21m/s m18=(m1+m)a,a=g/2=4.9m/s2 例:m,L的链条 求:下落x时链条对地面的作用力 解:方法1: V-2gx 静压力E。=Pg=m坚 L (dm.g-F )dt dm(0-V) a dm =-dm2gx dm…g R-留ap”er=p2 2mgx F=F+F= 3mgx L 方法2:P=(L-x)pP g-r-gL-9a 、4 V+(L-x)p mg =-pV2+(L-x)pg =-p2gx+mg-xpg 3mgx F-30F- 3mgx L
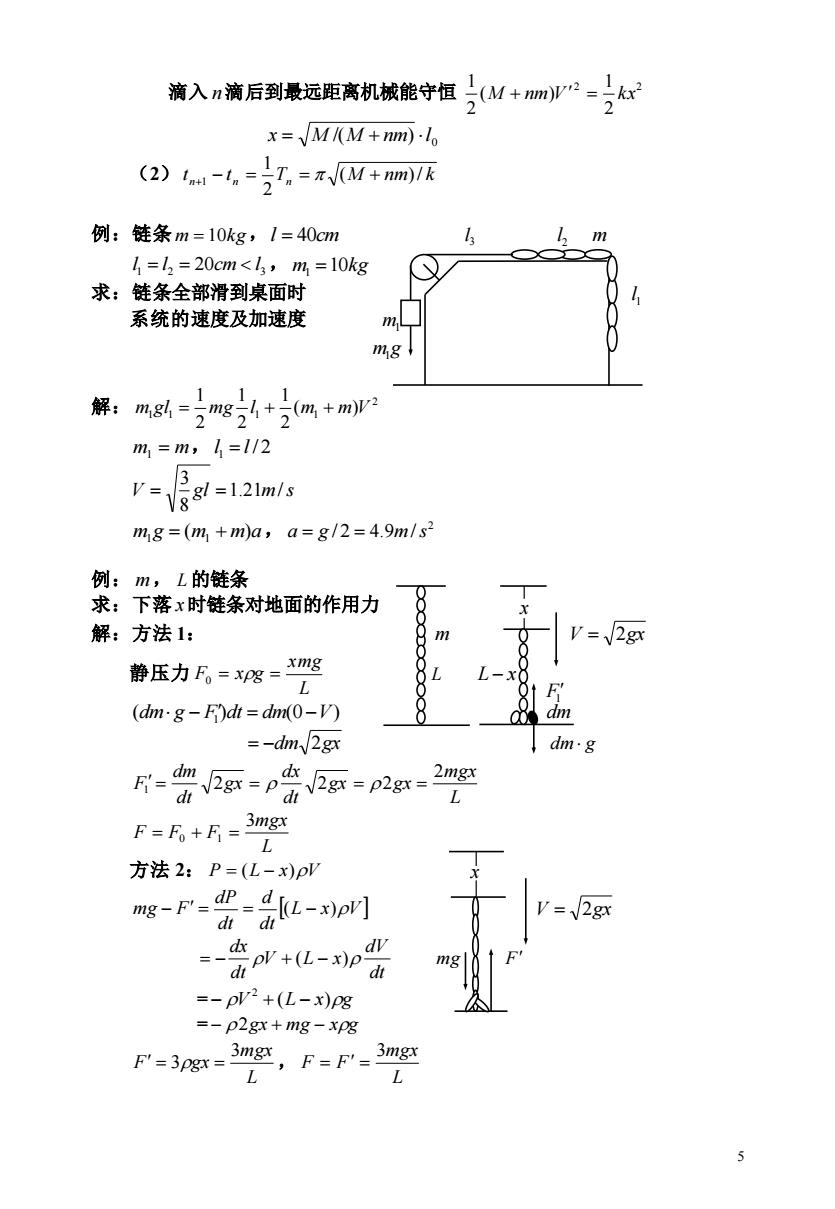
5 滴入 n 滴后到最远距离机械能守恒 2 2 2 1 ( ) 2 1 M + nm V = kx 0 x = M /(M + nm) l (2) t t T M nm k n n n ( )/ 2 1 +1 − = = + 例:链条 m = 10kg,l = 40cm 3 l 2 l m 1 2 20 3 l = l = cm l , m1 =10kg 求:链条全部滑到桌面时 1 l 系统的速度及加速度 m1 m g1 解: 2 1 1 1 1 ( ) 2 1 2 1 2 1 m gl = mg l + m + m V m1 = m, l 1 = l / 2 V gl 1.21m/s 8 3 = = m1g = (m1 + m)a, 2 a = g / 2 = 4.9m/s 例: m, L 的链条 求:下落 x 时链条对地面的作用力 解:方法 1: m V = 2gx 静压力 L xmg F0 = xg = L L − x ( ) (0 ) dm g − F1 dt = dm −V dm = −dm 2gx dm g L mgx gx gx dt dx gx dt dm F 2 1 = 2 = 2 = 2 = L mgx F F F 3 = 0 + 1 = 方法 2: P = (L − x)V L x V dt d dt dP mg − F = = ( − ) V = 2gx dt dV V L x dt dx = − + ( − ) mg F = V (L x)g 2 − + − = − 2gx + mg − xg L mgx F gx 3 = 3 = , L mgx F F 3 = = x x F1
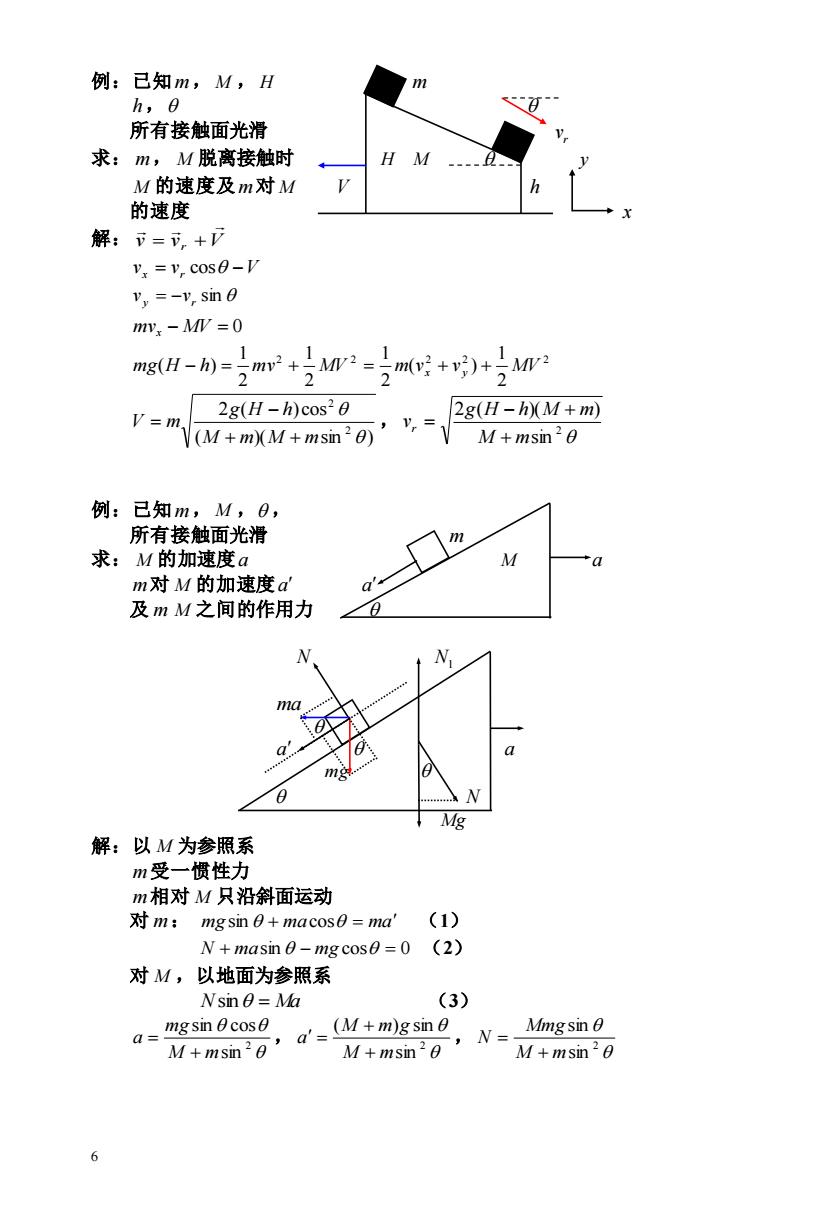
例:已知m,M,H h,0 所有接触面光滑 求:m,M脱离接触时 H M M的速度及m对M 的速度 解:下=下,+☑ V =V.cos-V Vy =-V sin e mv,-MV=0 W(4=(-H)w V=m 2g(H-h)cos20 ,= 2g(H-h)(M+m) (M+m)(M+msin20) M+msin20 例:已知m,M,B, 所有接触面光滑 m 求:M的加速度a M m对M的加速度ad Q 及mM之间的作用力 ma 9 Mg 解:以M为参照系 m受一惯性力 m相对M只沿斜面运动 m:mgsin 0+macos=ma'(1) N+masin 0-mgcos0=0 (2) 对M,以地面为参照系 Nsin0=Ma (3) a=mgsin 0cos M+msin2乙,N=gsnA M+msin20 6
6 例:已知 m, M , H m h, 所有接触面光滑 r v 求: m, M 脱离接触时 H M y M 的速度及 m 对 M V h 的速度 x 解: v vr V = + vx = vr cos −V vy = −vr sin mvx − MV = 0 2 2 2 2 2 2 1 ( ) 2 1 2 1 2 1 mg(H − h) = mv + MV = m vx + vy + MV ( )( sin ) 2 ( ) cos 2 2 M m M m g H h V m + + − = , 2 sin 2 ( )( ) M m g H h M m vr + − + = 例:已知 m, M , , 所有接触面光滑 m 求: M 的加速度 a M a m 对 M 的加速度 a a 及 m M 之间的作用力 N N1 ma a a mg N Mg 解:以 M 为参照系 m 受一惯性力 m 相对 M 只沿斜面运动 对 m : mg sin + macos = ma (1) N + masin − mg cos = 0 (2) 对 M ,以地面为参照系 Nsin = Ma (3) 2 sin sin cos M m mg a + = , 2 sin ( ) sin M m M m g a + + = , 2 sin sin M m Mmg N + =