西安电子科技大学：《大学物理》课程教学讲义（上）09 刚体定轴转动运动学

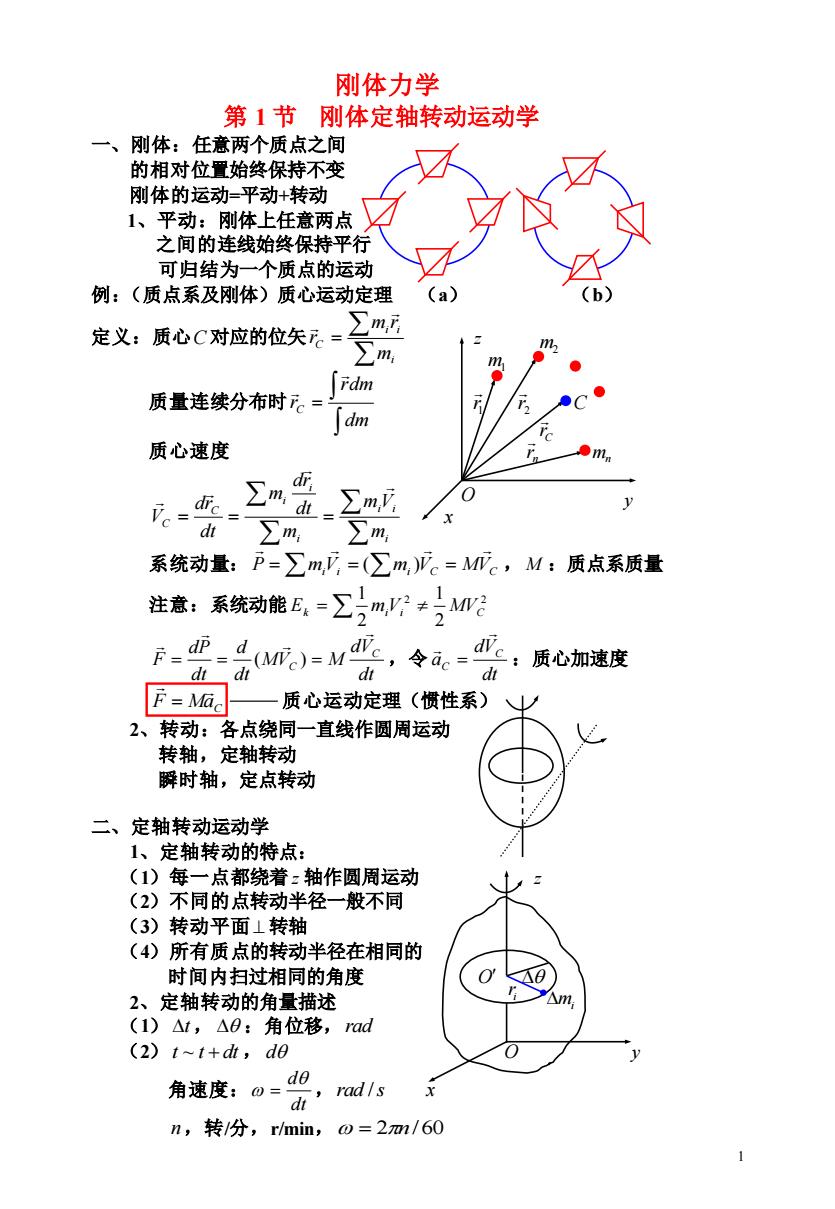
刚体力学 第1节刚体定轴转动运动学 一、刚体：任意两个质点之间 的相对位置始终保持不变 刚体的运动=平动+转动 1、平动：刚体上任意两点 之间的连线始终保持平行 可归结为一个质点的运动 例：（质点系及刚体)质心运动定理 a 定义：质心C对应的位矢。= mF m m Fdm 质量连续分布时下。= 《 dm 质心速度 灰、 ∑m,d ∑m, y d-∑m, ∑m 系统动量：P-∑m,了=（∑m,)Pe=MWc，M:质点系质量 注意：系统动能E:-∑m≠M阳 F-亚=（w。)=M亚，令。-亚：质心加速度 d dt d dt F=Ma。 质心运动定理（惯性系） 2、转动：各点绕同一直线作圆周运动 转轴，定轴转动 瞬时轴，定点转动 二、定轴转动运动学 1、定轴转动的特点： (1)每一点都绕着：轴作圆周运动 （2)不同的点转动半径一般不同 (3)转动平面1转轴 (4)所有质点的转动半径在相同的 时间内扫过相同的角度 2、定轴转动的角量描述 △vm. (1)△t,△0：角位移，ad (2)1~1+dt,d0 de 角速度：o= ，rad/s X dt n,转/分，r/min,o=2m/60

1 刚体力学 第 1 节 刚体定轴转动运动学 一、刚体：任意两个质点之间 的相对位置始终保持不变 刚体的运动=平动+转动 1、平动：刚体上任意两点 之间的连线始终保持平行 可归结为一个质点的运动 例：（质点系及刚体）质心运动定理 （a） （b） 定义：质心 C 对应的位矢   = i i i C m m r r   z 质量连续分布时   = dm rdm rC   1 r  2 r  C 质心速度 n r  mn     = = = i i i i i i C C m m V m dt dr m dt dr V     x 系统动量： P = miVi = mi VC = MVC     ( ) ，M ：质点系质量 注意：系统动能 =   2 2 2 1 2 1 Ek miVi MVC dt dV MV M dt d dt dP F C C     = = ( ) = ，令 dt dV a C C   = ：质心加速度 F MaC   = 质心运动定理（惯性系） 2、转动：各点绕同一直线作圆周运动 转轴，定轴转动 瞬时轴，定点转动 二、定轴转动运动学 1、定轴转动的特点： （1）每一点都绕着 z 轴作圆周运动 z （2）不同的点转动半径一般不同 （3）转动平面 ⊥ 转轴 （4）所有质点的转动半径在相同的 时间内扫过相同的角度 O  2、定轴转动的角量描述 （1） t ，  ：角位移， rad （2） t ~ t + dt ， d O y 角速度： dt d  = ，rad /s x n，转/分，r/min， = 2n/ 60 C r  i r mi m1 m2 O y

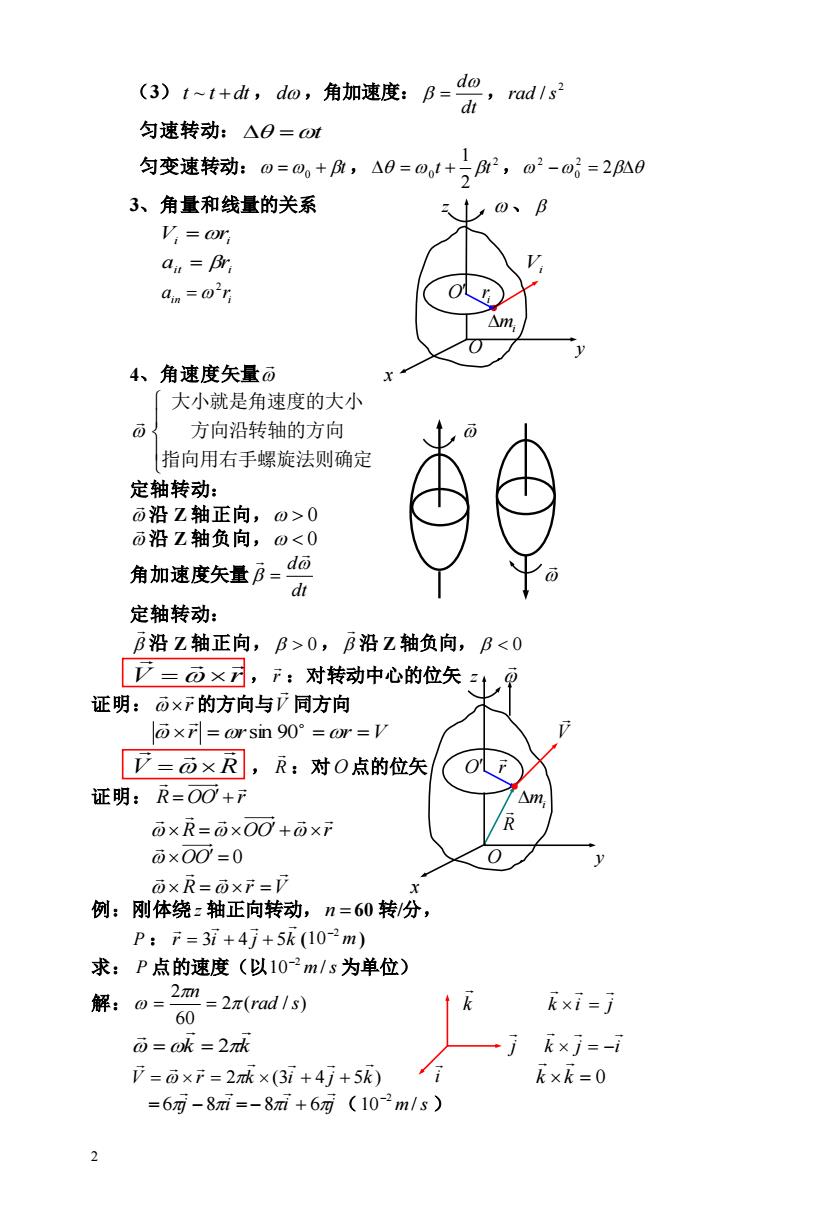
(3)t~t+h,do,角加速度：B=d0, dh’ad/s2 匀速转动：△日=t 匀变速转动：0=0+A,A0=0,1+)pm2,02-=20 3、角量和线量的关系 0、B V=or a=Br an=0' △m 4、角速度矢量0 大小就是角速度的大小 方向沿转轴的方向 指向用右手螺旋法则确定 定轴转动： 0沿Z轴正向，o>0 0沿Z轴负向，00,B沿Z轴负向，B<0 [=可×，F:对转动中心的位矢1可 证明：×r的方向与7同方向 o×f=orsin90°=or=V V=可×R,R:对O点的位矢 证明：R=OO+ △m oxR=o×OO+o× R ò×O0=0 而×R=而xr= 例：刚体绕z轴正向转动，n=60转/分， P:r=3i+4i+5k(10-2m) 求：P点的速度（以10-2m/s为单位） 解：0=2=2xad1s) k×i=-j 60 ō=0k=2k kxj=-i 7=o×F=2k×(3i+4j+5k) k×k=0 =6列-8=-8+6列（10-2m/s) 2

2 （3） t ~ t + dt ， d ，角加速度： dt d  = ， 2 rad /s 匀速转动：  =t 匀变速转动：  = + t 0 ， 2 0 2 1  = t + t ， − = 2 2 0 2 3、角量和线量的关系 z  、  i i V =r it i a = r Vi in i a r 2 = O i r mi O y 4、角速度矢量   x        指向用右手螺旋法则确定 方向沿转轴的方向 大小就是角速度的大小   定轴转动：   沿 Z 轴正向，   0   沿 Z 轴负向，   0 角加速度矢量 dt d    =   定轴转动：   沿 Z 轴正向，   0 ，   沿 Z 轴负向，   0 V r    = ， r  ：对转动中心的位矢 z   证明： r    的方向与 V  同方向  r =r =r =V    sin 90 V  V R    = ， R  ：对 O 点的位矢 O r  证明： R OO r   =  + mi R OO r       =  + OO = 0  O y R r V       = = x 例：刚体绕 z 轴正向转动， n = 60 转/分， P ： r i j k     = 3 + 4 + 5 ( m 2 10− ) 求： P 点的速度（以 10 m /s −2 为单位） 解： 2 ( / ) 60 2 rad s n    = = k  k i j     = k k     = = 2 j  k j i     = − V r 2 k (3i 4 j 5k )        =   =   + + i  k  k = 0   = j i   6 −8 = i j   −8 + 6 （ 10 m /s −2 ） R 

第2节力矩 X [Frsin 定义：力F对z轴的力矩M= Fd d:力臂 Fr 定义：力F对z轴的力矩矢量M=F×F F:F的作用点对其转动中心的位矢 M=M=rFsin,方向：F×F 牛[顿]米(N·m),MLT-2 定轴转动： M沿Z轴正向，M>0,M沿Z轴负向，M<0 说明： 1、如果F不在其作用点的转动平面内 F：和转轴/的分量 F：和转轴⊥的分量 规定：F对z轴的力矩为零 定义：力F对：轴的M(F)=F×F 2、力的作用线通过转轴或与转轴 平行，则力对轴的力矩为零 3、同一个力对不同的轴力矩一般不同 4、刚体受到的合力矩等于每个力矩的矢量和 M=M,+M2+…+M 或用标量式（定轴转动)M=M1+M,…+M 刚体：合力矩=力矩之和≠合力的力矩 5、重力矩等于全部重量 集中在重心时的重力的力矩 M=。xG ↓G=mg 3

3 第 2 节 力 矩 z Ft F  F  O r   O r  A d A O y x 定义：力 F  对 z 轴的力矩      = F r Fd Fr M t sin  d ：力臂 定义：力 F  对 z 轴的力矩矢量 M r F    =  r  ： F  的作用点对其转动中心的位矢 M = M = rF sin   ，方向： r F    牛[顿]米( N m )， 2 −2 ML T 定轴转动： M  沿 Z 轴正向， M  0， M  沿 Z 轴负向， M  0 说明： 1、如果 F  不在其作用点的转动平面内 z F  F//  ：和转轴//的分量 F//  F⊥  ：和转轴 ⊥ 的分量 F⊥  规定： F//  对 z 轴的力矩为零 r  定义：力 F  对 z 轴的 =  F⊥ M F r     ( ) 2、力的作用线通过转轴或与转轴 平行，则力对轴的力矩为零 3、同一个力对不同的轴力矩一般不同 4、刚体受到的合力矩等于每个力矩的矢量和 M M M Mn      = 1 + 2 + + 或用标量式（定轴转动） M = M1 + M2 + Mn 刚体：合力矩=力矩之和  合力的力矩 5、重力矩等于全部重量 O 集中在重心时的重力的力矩 G r  G M rG G    =  G mg   =

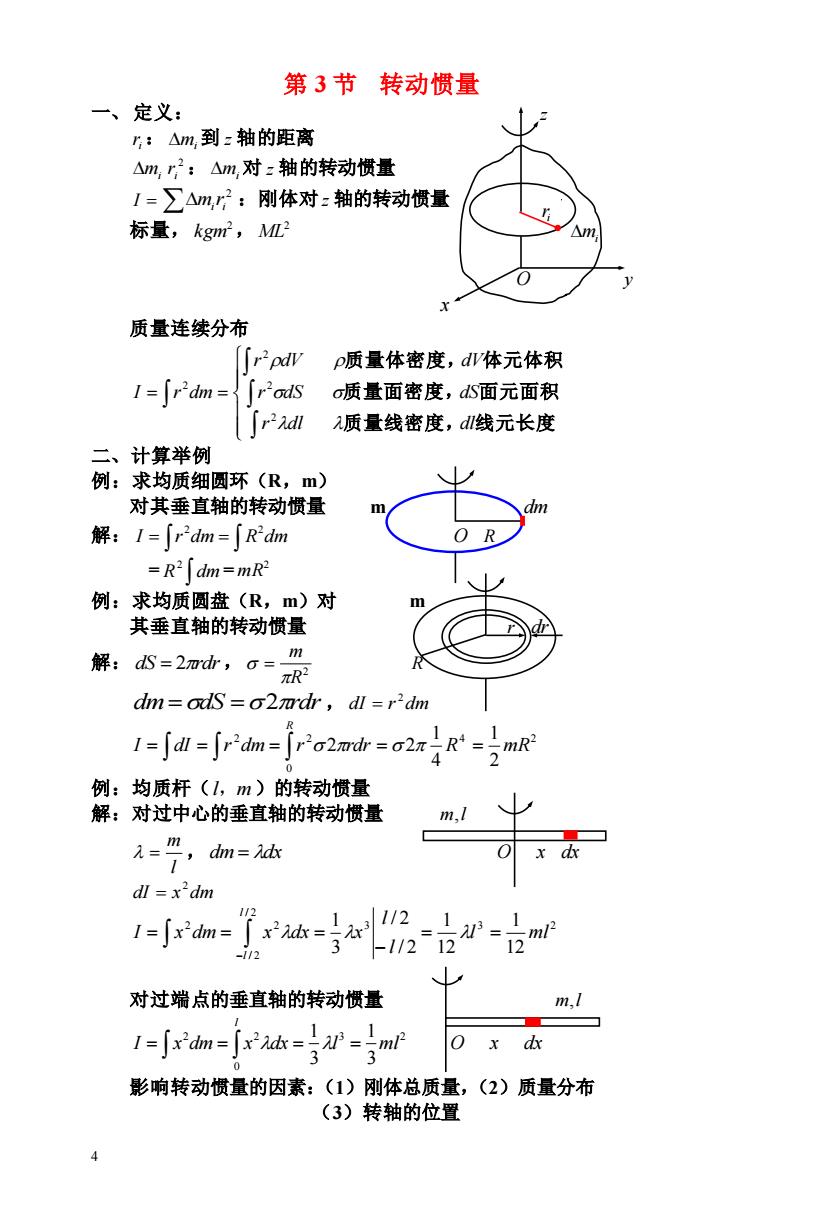
第3节 转动惯量 一、定义： ：△m,到z轴的距离 △m,r,2：△m,对z轴的转动惯量 1-∑△m,2:刚体对：轴的转动惯量 标量，kgm2,ML △m X 质量连续分布 「r2pdw P质量体密度，dWV体元体积 1=∫r2dm= 「r2odS o质量面密度，dS面元面积 「r2dl 质量线密度，d线元长度 二、计算举例 例：求均质细圆环(R,m) 对其垂直轴的转动惯量 解：I-rdm=∫Rdmn =R2∫dm=mR2 例：求均质圆盘(R,m)对 其垂直轴的转动惯量 解：S=2md,。=m 2 dm=odS=o2ndr,dl=r'dm I=∫dl=jrdm=jr2a2mt=o2πR4-mR2 例：均质杆（1，m)的转动惯量 解：对过中心的垂直轴的转动惯量 m,1 dm=Adx dl xdm 3 -1/2121 12 -1/2 对过端点的垂直轴的转动惯量 m.l I-ftn-ids-P-wp x dx 31 影响转动惯量的因素：(1)刚体总质量，(2)质量分布 (3)转轴的位置

4 第 3 节 转动惯量 一、 定义： z i r ： mi 到 z 轴的距离 mi 2 i r ： mi 对 z 轴的转动惯量 I =  2 i i m r ：刚体对 z 轴的转动惯量 标量， 2 kgm ， 2 ML mi O y x 质量连续分布            = = 质量线密度， 线元长度 质量面密度， 面元面积 质量体密度， 体元体积 r dl dl r dS dS r dV dV I r dm       2 2 2 2 二、计算举例 例：求均质细圆环（R，m） 对其垂直轴的转动惯量 m dm 解：   I = r dm = R dm 2 2 O R =  R dm 2 = 2 mR 例：求均质圆盘（R，m）对 m 其垂直轴的转动惯量 r dr 解： dS = 2rdr ， 2 R m   = R dm =dS =2rdr ， dI r dm 2 =    = = = = = R I dI r dm r rdr R mR 0 2 2 4 2 2 1 4 1  2  2 例：均质杆（ l，m ）的转动惯量 解：对过中心的垂直轴的转动惯量 m,l l m  = ， dm = dx O x dx dI x dm 2 =   − = = − = = = / 2 / 2 2 2 3 3 2 12 1 12 1 / 2 / 2 3 1 l l l ml l l I x dm x dx x  对过端点的垂直轴的转动惯量 m,l 3 2 0 2 2 3 1 3 1 I x dm x dx l ml l = = = =     O x dx 影响转动惯量的因素：（1）刚体总质量，（2）质量分布 （3）转轴的位置 i r

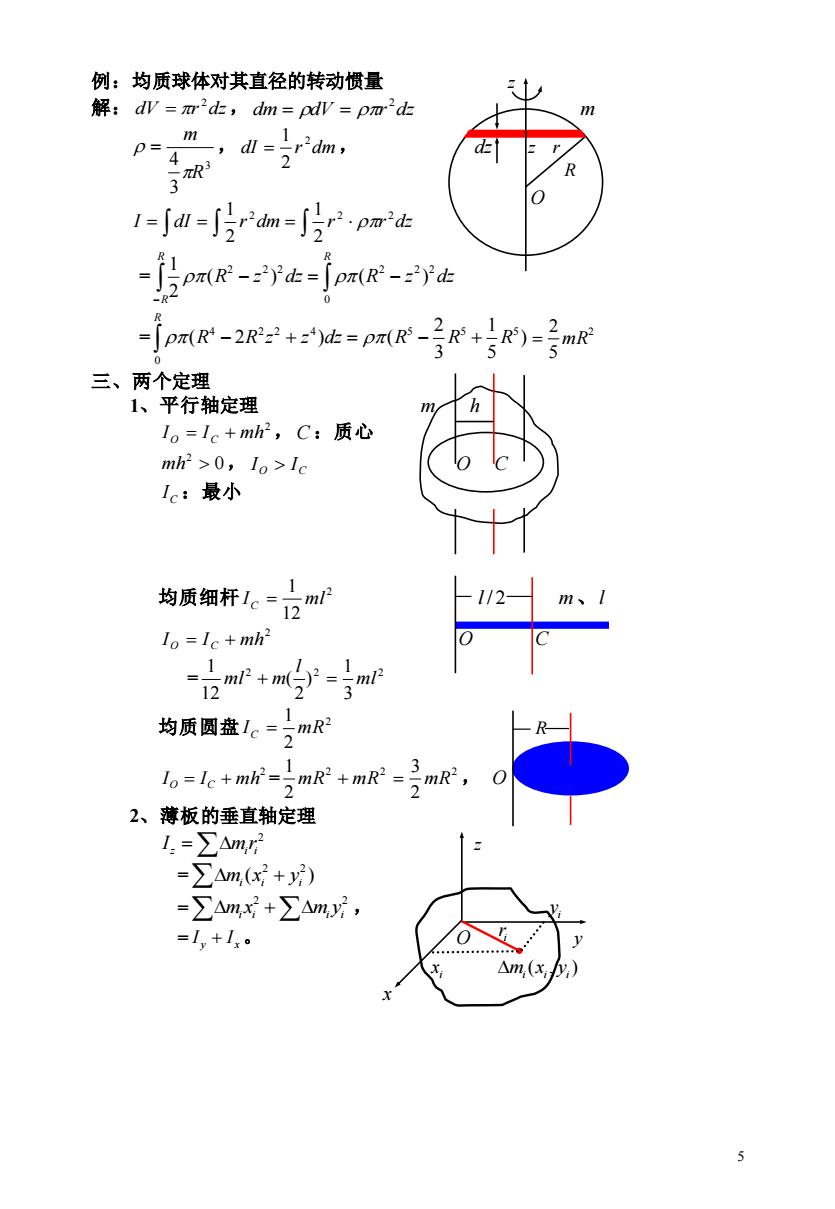
例：均质球体对其直径的转动惯量 解：dV=mr2d,dm=pdW=pm2d正 m,dl=r'dm, m p= d 3 4 2 1=∫a=片r2dm=∫2pmt -o(R( -JpT(R'-2R2+2d=pX(R-3R+IR)= 3 mR2 三、两个定理 1、平行轴定理 Io=Ic+mh2,C:质心 mh2>0,1o>1c Ic:最小 均质细杆1。= n12 12 m、 i Io Ic+mh2 0 12m+m( 1 3 均质圆盘1。= lo=le+mli-mR'+mR= 2mR,O 2、薄板的垂直轴定理 L=∑Am =∑Am,(x+y) =∑Am,x+∑Am,y, =1,+1x0 △m(x:y 5

5 例：均质球体对其直径的转动惯量 z 解： dV r dz 2 =  ， dm dV r dz 2 =  =  m 3 3 4 R m   = ， dI r dm 2 2 1 = ， dz z r    I = dI = r dm = r  r dz 2 2 2 2 1 2 1  =   − − = − R R R R z dz R z dz 0 2 2 2 2 2 2 ( ) ( ) 2 1   =  − + = − + R R R z z dz R R R 0 4 2 2 4 5 5 5 ) 5 1 3 2 ( 2 ) ( 2 5 2 = mR 三、两个定理 1、平行轴定理 m h 2 I O = IC + mh ， C ：质心 0 2 mh  ， O C I  I O C C I ：最小 均质细杆 2 12 1 I ml C = l / 2 m、l 2 I O = IC + mh O C = 2 2 2 3 1 ) 2 ( 12 1 ml l ml + m = 均质圆盘 2 2 1 IC = mR R 2 IO = IC + mh = 2 2 2 2 3 2 1 mR + mR = mR ， O 2、薄板的垂直轴定理 = 2 z i i I mr z = ( + ) 2 2 i i i m x y = + 2 2 i i i i m x m y ， i y = y x I + I 。 O y i x ( , ) i i i m x y x i r O R