11一3磁通量 磁高斯定理 一、磁力线 B= ds B等于通过和磁场 相垂直的单位面积 ds 上的磁力线条数 磁力线 性质: “磁力线都是闭合曲线,并与电流相互套合, 磁力线的回绕方向与电流方向满足右手定则。” 二、磁通量 穿过曲面S的磁力线 条数Φm:磁通量(标量) d BdS BdS cos=B.dS dΦm=BdS Φn=∫dmn=∫B.ds S:Tm2=Wb(韦伯) 三、 磁高斯定理 2 闭合曲面: 中n=fB. 取闭合曲面的外法线方向 为正法线方向 -0 磁高斯定理 磁场是无源场 例:求① a d 解:dΦn=B-aS=BcosaS=1k 2nx -j-装= 2π 1
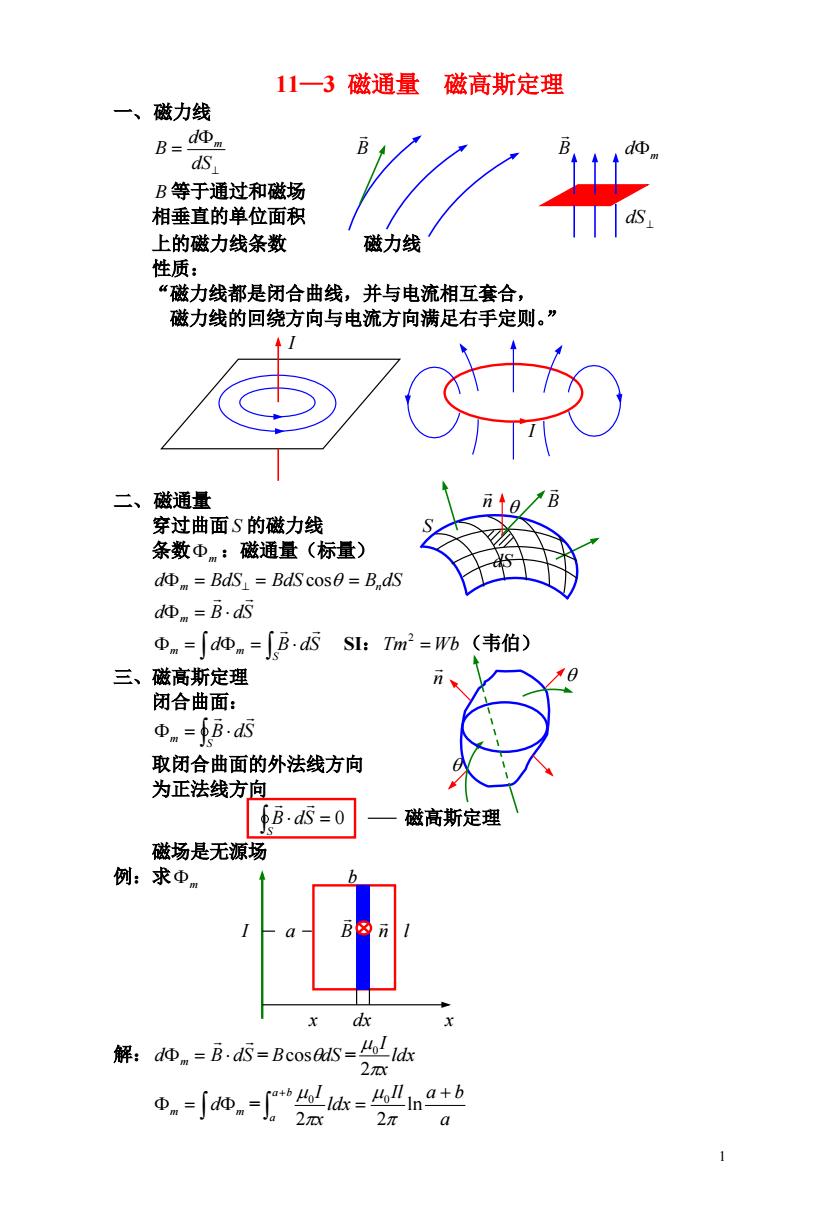
1 11—3 磁通量 磁高斯定理 一、磁力线 dS d B m B B m d B 等于通过和磁场 相垂直的单位面积 dS 上的磁力线条数 磁力线 性质: “磁力线都是闭合曲线,并与电流相互套合, 磁力线的回绕方向与电流方向满足右手定则。” I I 二、磁通量 n B 穿过曲面 S 的磁力线 S 条数m :磁通量(标量) d BdS BdS B dS m n cos d m B dS SI: (韦伯) S m d m B dS Tm Wb 2 三、磁高斯定理 n 闭合曲面: S m B dS 取闭合曲面的外法线方向 为正法线方向 0 磁高斯定理 S B dS 磁场是无源场 例:求 m b I a B n l x dx x 解:d m B dS = = BcosdS ldx x I 2 0 = m m d a Il a b ldx x a b I a ln 2 2 0 0 dS
例:求Φm b n dx ⑧ B月厅 解:dΦn=B.dS=BcosadS=xhd=,h xdx 2n r 2πx2+(△Z) -0-小广2流 -2me+wr-a2 4π a2+(△Z)2 例:求Φm(t) 2ao(常数) -b 2a 解:等效面积 0 a B=om,Φn0=42aln2 2 =a2+b2+2abcosot,n2=a2+b2-2abcosot ①.0=a1n+6+2 abcosmt 2π a2+b2-2abcosot 2
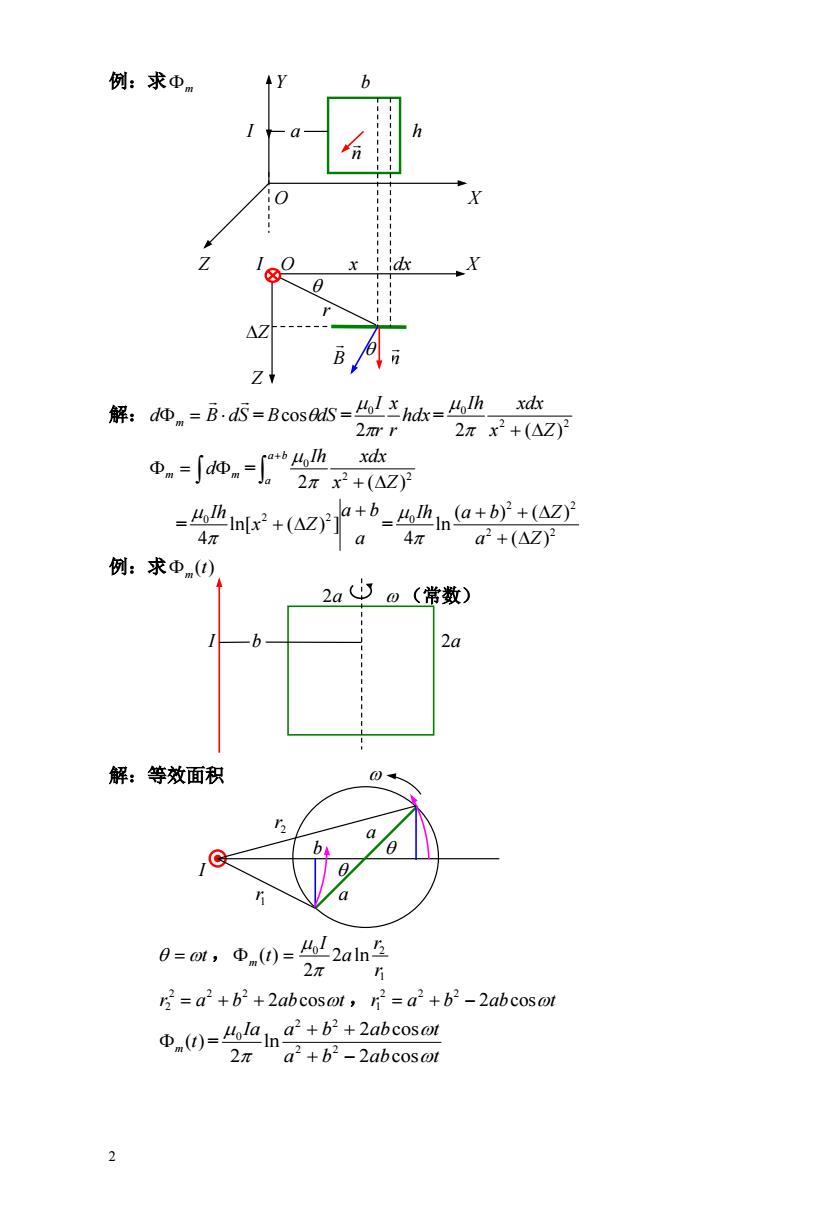
2 例:求 m Y b I a h n O X Z I O x dx X r Z B n 解:d m B dS = = = BcosdS hdx r x r I 2 0 2 2 0 2 x ( Z) Ih xdx = m m d a b a x Z Ih xdx 2 2 0 2 ( ) = = a a b x Z Ih ln[ ( ) ] 4 0 2 2 2 2 2 2 0 ( ) ( ) ( ) ln 4 a Z Ih a b Z 例:求 (t) m 2a (常数) I b 2a 解:等效面积 2r b I 1r a t , 1 0 2 2 ln 2 ( ) r r a I t m r2 2 a 2 b 2 2abcost ,r a b 2abcost 2 2 2 1 m (t) = a b ab t Ia a b ab t 2 cos 2 cos ln 2 2 2 2 2 0 a Z