11一5磁场对电流的作用 第1节安培定律 dF Idl x B 安培定律 dF IdlBsin0 方向:dFLΠ(ldi,B) Idl 指向:右手螺旋法则 公 F=∫d=[IdixB Oxyz,dF=dFi+dF j+dF.k F=∫dE,F,=∫dE,F=∫df F=Fi+Fj+Fk,一般情况下,F≠dF 例: 解:F=∫dxB 均匀B =0)xB =labx B F=IabBsin0 B:ab与B的夹角 a 例: 均匀B X X X 解:F=f团×B=⑤)×B=0 例:计算导线受力 均匀B× R × × X 解:F=Iab×B,F=labBsin0=I2l+R)B,方向个 1
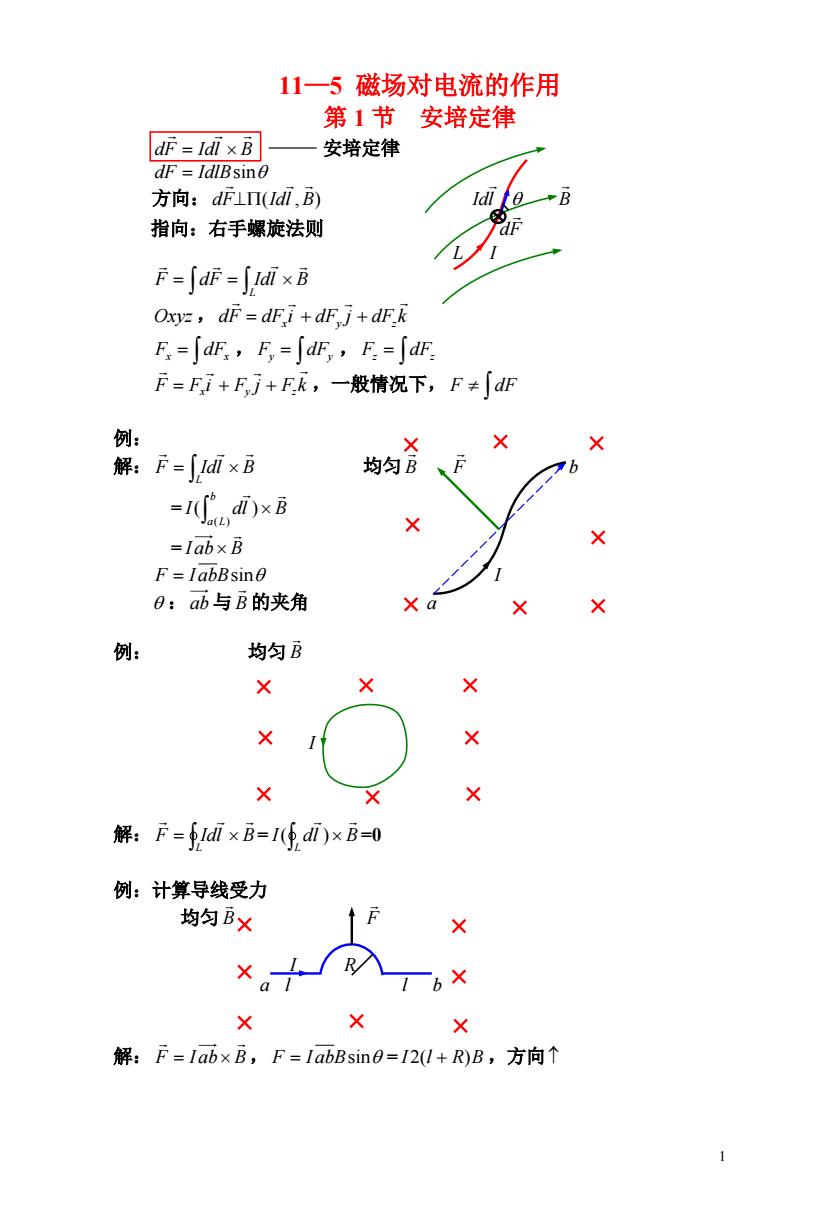
1 11—5 磁场对电流的作用 第 1 节 安培定律 dF Idl B 安培定律 dF IdlBsin 方向:dF (Idl ,B) Idl B 指向:右手螺旋法则 dF L I L F dF Idl B Oxyz ,dF dF i dF j dF k x y z Fx dFx , Fy dFy , Fz dFz F Fxi Fy j Fzk ,一般情况下, F dF 例: 解: 均匀 L F Idl B B F b = b a L I dl B ( ) ( ) = I ab B F I abBsin I :ab 与 B 的夹角 a 例: 均匀 B I 解: = =0 L F Idl B L I dl B ( ) 例:计算导线受力 均匀 B F I R a l l b 解: F I ab B, = ,方向 F I abBsin I 2(l R)B

例:正三角形线圈受力 B a I,dl b- I,dl df -8 x dx x 解:AB:dF=,dB=1,d,方向← 2πb F-a-地=治2,方涧← 2πb BC:dF=I,dlB Fc=∫d=∫l,dB=mw44 2n sin60 6+5 a V3π ,与:轴夹角60 同理,F4c=Fc,与x轴夹角(-60°) 合力:F=-FAB+Fac cos60°+Fc cost(-60) =-FAB FBC -0+44n6+。 -a 2b√3π"b F,=0 2
2 例:正三角形线圈受力 B a dF I dl 2 1I b 2 I I dl 2 C dF B dF A x dx x 解:AB:dF I 2dlB = ,方向 b I I dl 2 0 1 2 FAB dF = dl = ,方向 b B I I A 2 0 1 2 b I I a 2 0 1 2 BC:dF I 2dlB = FBC dF I 2dlB 2 sin 60 sin 60 0 1 2 dx x b a I I b = ,与 轴夹角 b b a I I 2 3 ln 3 0 1 2 x 60 同理, FAC FBC ,与 x 轴夹角( 60 ) 合力: cos60 cos( 60 ) Fx FAB FBC FAC = FAB FBC = + b I I a 2 0 1 2 b b a I I 2 3 ln 3 0 1 2 Fy 0
第2节磁场对载流线圈的作用 一、均匀磁场中的载流线圈 P.ISn a Fas=labBsin(0) 2 labBcos0, 均匀B Fbe =IbcB n F.=fcdBsin) =IcdBcos0, Fa=IdaB 合力F=0 M=F Labsino +Fiabsine, Fabsin=IdaB absin=ISBsin0=P Bsin0 M=Pn×B 讨论(1)下∥B F=0,M=0 P稳定平衡 (2)P⊥B F=0,M=PB O⑧ (3)P I/(-B) F=0,M=0 不稳定平衡 说明:均匀磁场,M=P×B适用于任意形状的线圈 M=P×E 二、非均匀磁场中的线圈 线圈受到的合磁力及力矩不一定为零 3
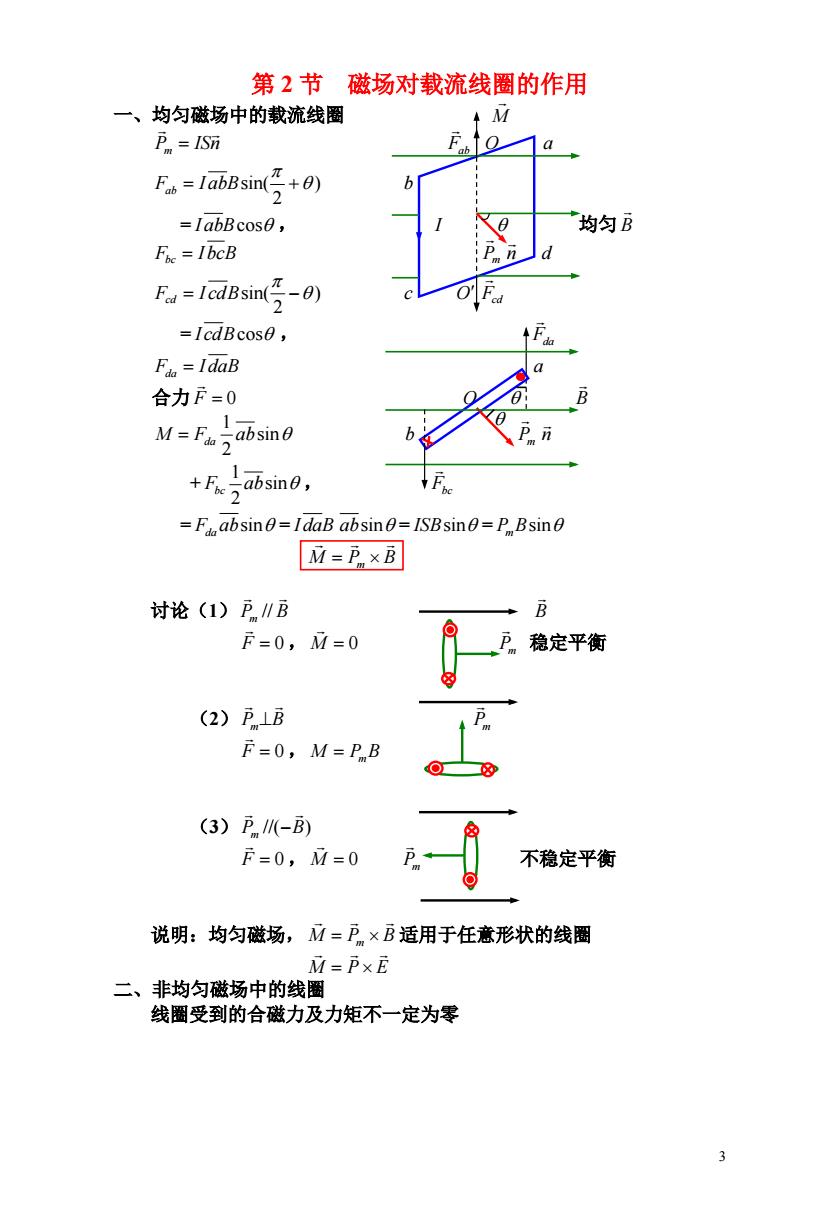
3 第 2 节 磁场对载流线圈的作用 一、均匀磁场中的载流线圈 M P ISn m Fab O a ) 2 sin( Fab I abB b = I abBcos , I 均匀 B F IbcB bc Pm n d ) 2 sin( Fcd I cdB c O Fcd = I cdBcos , Fda F I daB da a 合力 F 0 O B sin 2 1 M Fda ab b Pm n + sin , 2 1 Fbc ab Fbc = Fda absin = I daB absin = ISBsin = PmBsin M Pm B 讨论(1) P B m // B F 0 , 稳定平衡 M 0 Pm (2) P B m Pm F 0 , M PmB (3) P //( B) m F 0 , 不稳定平衡 M 0 Pm 说明:均匀磁场, M Pm B 适用于任意形状的线圈 M P E 二、非均匀磁场中的线圈 线圈受到的合磁力及力矩不一定为零
第3节 磁力的功 一、磁场对载流导线的功 均匀BX d a C b X F=IIB A=Faa'=IIB(da'-da)=I(Blda'-Blda) =I(④m2-Φnmi)=IAΦm 二、磁场对载流线圈的功 均匀B 卫m=1S7 M=pn×B,M=P.Bsin0 dA=M(-de)=P Bsine(-de)=ISBsin0(-de) =Id(BS cos0)=IdΦ A=∫4=。一磁力作功的一般表达式 若1恒定,A=心dm.=1④a-中i)=p. 例: ↑M 均匀B 求:(1)M=?(2)线圈转过90°,A=? 解:(1)M=Pn×B,M=P.Bsin0=I二πRB,方向个 (2)A=IA@-1RB 4
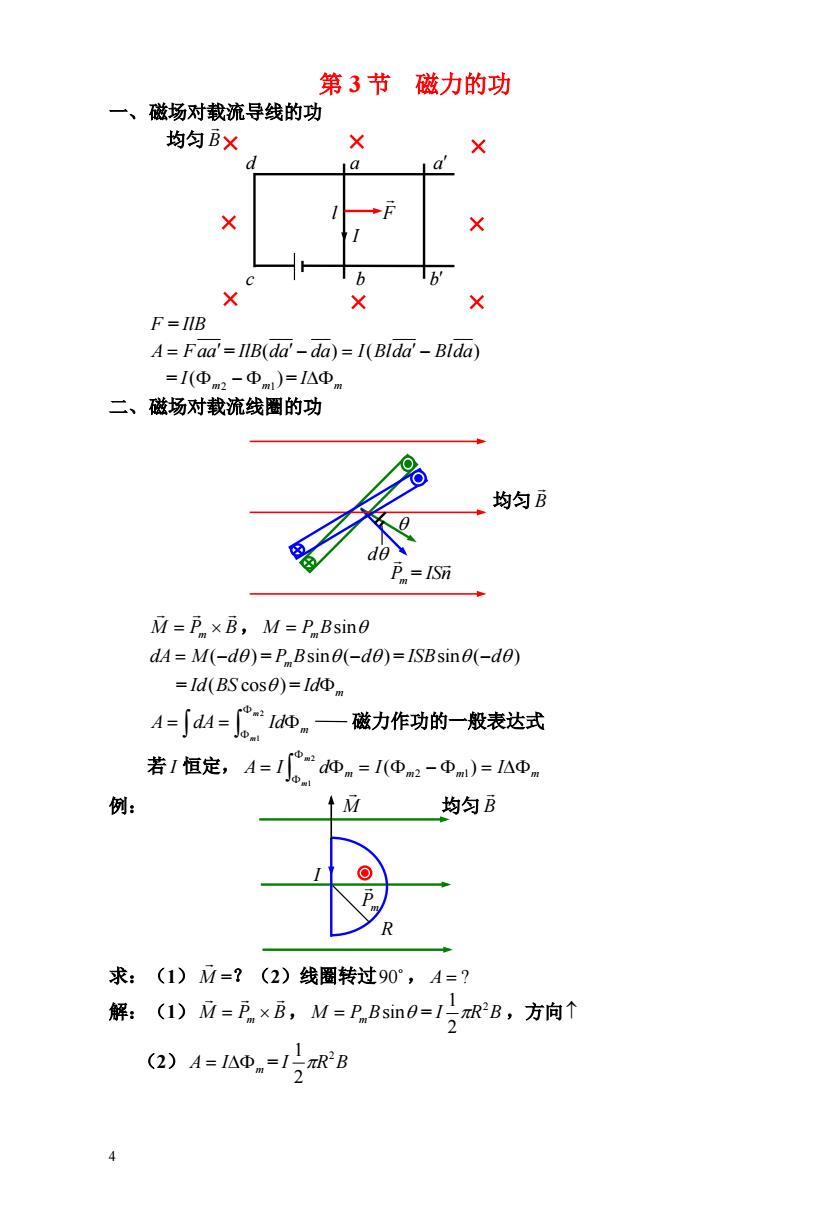
4 第 3 节 磁力的功 一、磁场对载流导线的功 均匀 B d a a l F I c b b F = IlB A Faa= IlB(da da) I(Blda Blda) = ( ) = m2 m1 I m I 二、磁场对载流线圈的功 均匀 B Pm = ISn M Pm B, M PmBsin dA M (d ) = PmBsin (d ) = ISBsin (d ) = Id(BS cos ) = m Id 磁力作功的一般表达式 2 1m m m A dA Id 若 I 恒定, m m m m A I d I I m m ( ) 2 1 2 1 例: M 均匀 B I Pm R 求:(1) M =?(2)线圈转过 , 90 A ? 解:(1) M Pm B, = ,方向 M PmBsin I R B 2 2 1 (2) A Im = I R B 2 2 1 d
例: 均匀B × X 求:张力 解: R T F=12RB=2T,T=IRB 例:带电圆盘(R、o=k知) 均匀B 0 求:M 解:M=Pn×B dS =2mdr,dq o2nrdr=kr2mdr 山-2元的=g2ow-o咖h 2元 dPn=dS=π2okr2dr=πokr'dr P.-JdP.rokr'droR M=P,Bsim0=kRB,方向个
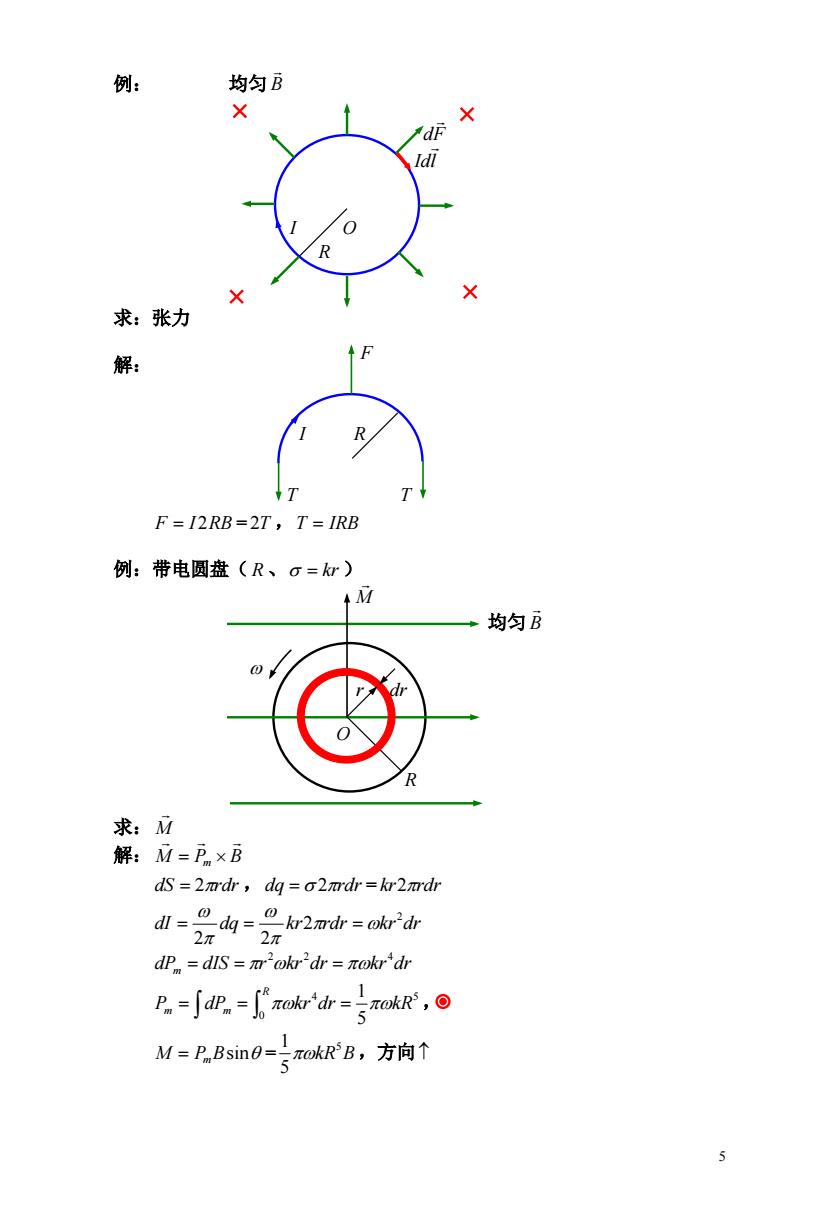
5 例: 均匀 B dF Idl I O R 求:张力 解: I R F I 2RB = 2T ,T IRB 例:带电圆盘( R 、 kr ) M 均匀 B r dr O R 求: M 解: M Pm B dS 2rdr ,dq 2rdr = kr2rdr dI dq kr rdr kr dr 2 2 2 2 dP dIS r kr dr kr dr m 2 2 4 5 , 0 4 5 1 P dP kr dr kR R m m M PmBsin = kR 5B ,方向 5 1 F T T