西安电子科技大学：《大学物理》课程教学讲义（下）12-2 动生电动势

12一2动生电动势 导体切割磁力线所产生 Fm=ef×B BX E鞋=Fm1e=f×B, eo=E生di -f(xB)-d7, 以积分的方向：电动势的正方向 闭合回路：e=fW×B)dl 例：求电动势 BX b↑V×BX 6=k0x d匀速7 xcosan -VBsin pcosd =Bdl=B1>0,a→6 b端电势高，Ub=-6 例： 恒定均匀B× ou=g0×Bdi A dr -[VB(-1)dl, dl --orBdr, 1 =--B12<0 × A→0，UoA=-8o4 例：法拉第圆盘 恒定均匀BX 二oBR2<0,A→O，Uo4=-8oa 1

1 12—2 动生电动势 导体切割磁力线所产生 F eV B m      B  E非  b E非 = ，  Fm e V B    /   dl V  E dl b a L ab       ( ) 非 = V B dl ， b a L       ( ) ( ) a Fm  以积分的方向：电动势的正方向 闭合回路：     L V B dl     ( ) 例：求电动势 B  b V B    V B dl b a L ab        ( ) ( )  l dl 匀速 =  V  V B dl b a L cos  ( )    = VB dl b a L sin cos  ( ) = VBdl = ， b a(L) VBl  0 a  b b 端电势高，Uab ab   例： 恒定均匀 B  V B dl A O OA         ( ) V  A = VB dl ， l ( 1) 0   r = rBdr ， l   0  V B    O = 0 2 1 2  Bl  A  O ，UOA OA   例：法拉第圆盘 恒定均匀 B   A O R 0， ， 2 1 2  OA   BR  A  O UOA OA   dr dl a Fm  

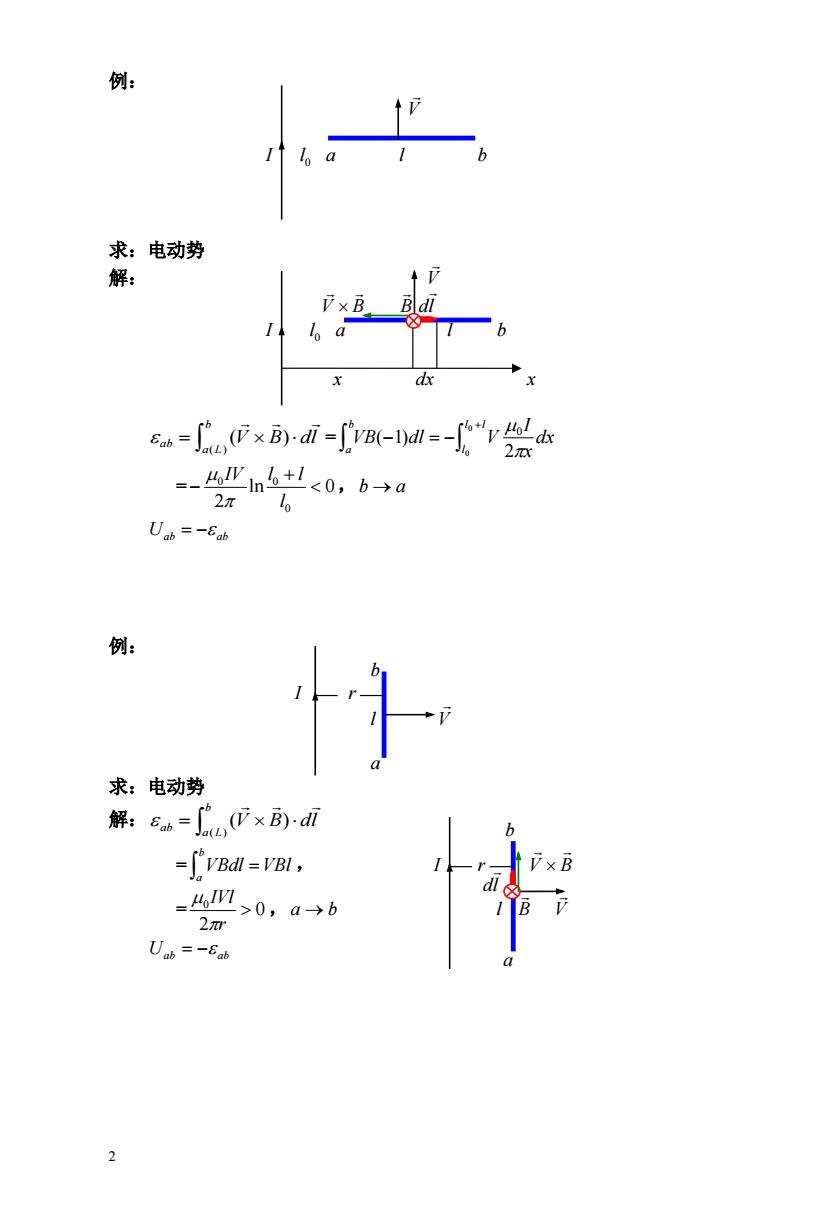
例： lo a 求：电动势 解： lo a b dx .(x -di-fv-d =-ain5+l0,a→b B 2n Uab=-Eab 2

2 例： V  I 0 l a l b 求：电动势 解： V  V B    B  dl I 0 l a l b x dx x V B dl = b a L ab        ( ) ( )  dx x I VB dl V l l l b a   2 ( 1) 0 0 0       = ln 0， 2 0 0 0    l IV l l   b  a Uab ab   例： b I r l V  a 求：电动势 解： V B dl b a L ab        ( ) ( )  = VBdl VBl ， b a   I r V B    = 0， 2 0  r IVl   a  b l B  V  Uab ab   dla b

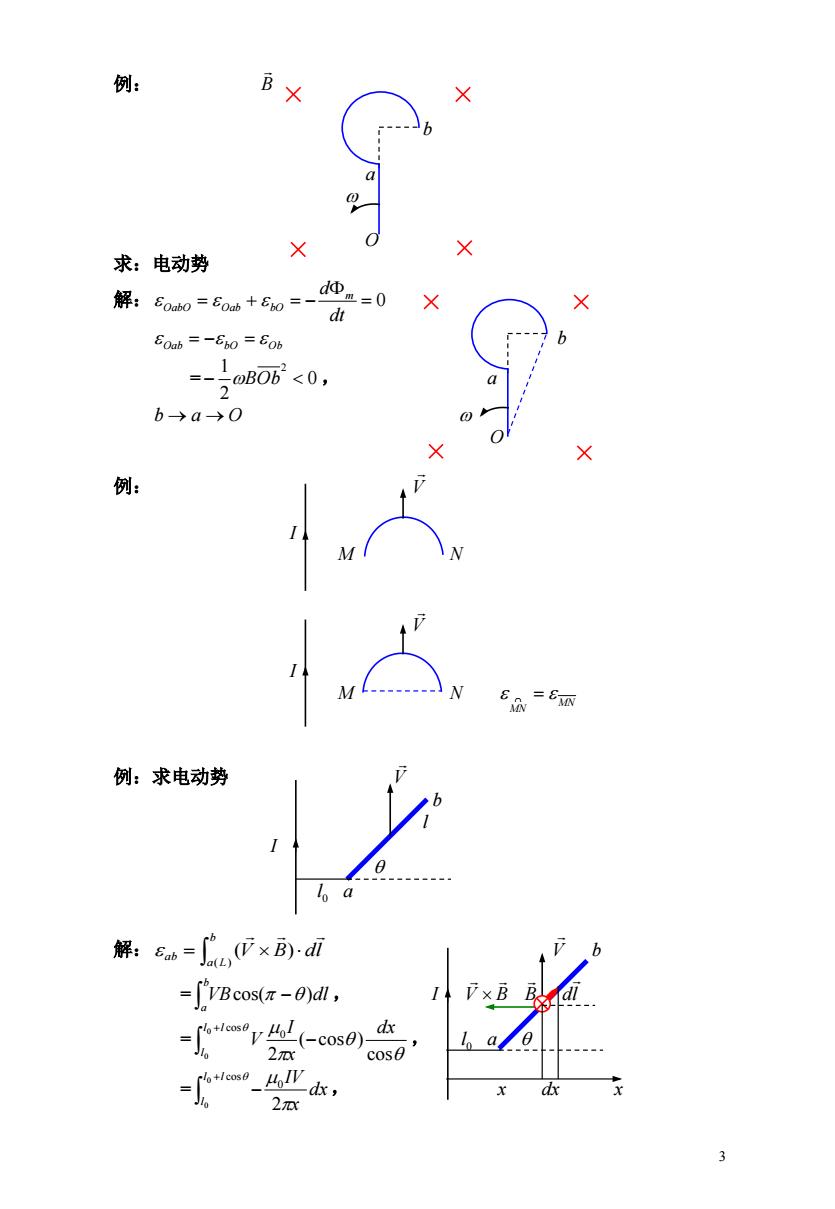
例： B 求：电动势 解：G0ab0=E0ab+60=- Φ =0 d × Eoab =-8b0 =E0b oB0b<0, 2 b→a→0 × 例： 例：求电动势 解：6w=,×B)-a b -[VBcos(-0dl, 2nx cos0 to -dx, dx 2n 3

3 例： B  b a  O 求：电动势 解：  0      dt d m OabO Oab bO    Oab bO Ob      b = 0 ， 2 1 2  BOb  a b  a  O  O 例： V  I M N V  I M N MN MN     例：求电动势 V  b l I  0 l a 解： V B dl b a L ab        ( ) ( )  V  b = ，   b aVBcos(  )dl I V B    B  dl = ，      cos ( cos ) 2 0 cos 0 0 dx x I V l l l    0 l a  = dx ， x l l IV l    2 0 cos 0 0    x dx x

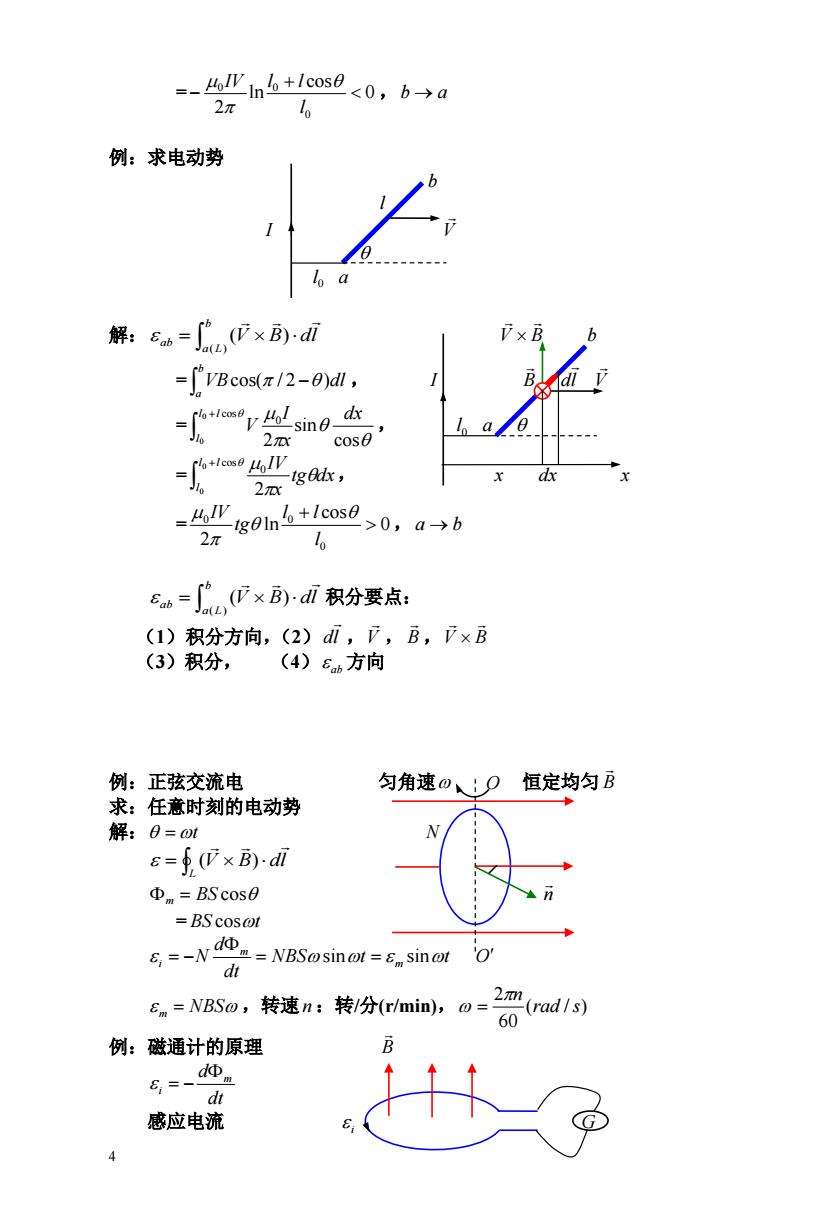
=-Y1nb+lcos00,a→b 2π g01n6+1cs 6b=W×di积分要点： (1)积分方向，(2)di,F,B,×B (3)积分， (4)6b方向 例：正弦交流电 匀角速0、：D恒定均匀B 求：任意时刻的电动势 解：0=o 6=fW×B)i Φm=BScose BS cosot 5=-N=NBSosinot=sinol dt En-NBSo,转速n:转/分(r/min),o= 2m (radls) 60 例：磁通计的原理 ￡-、地 _dt 感应电流

4 = 0 ， cos ln 2 0 0 0    l IV l l    b  a 例：求电动势 b l I V   0 l a 解： V B dl b a L ab        ( ) ( )  V B    b = ，   b a VBcos( / 2  )dl I B  dl V  = ，      cos sin 2 0 cos 0 0 dx x I V l l l  0 l a  = ，      cos 0 0 0 2 l l l tg dx x IV x dx x = 0， cos ln 2 0 0 0   l l l tg IV     a  b V B dl 积分要点： b a L ab        ( ) ( )  （1）积分方向，（2）dl ， ， ，  V  B  V B    （3）积分， （4） ab 方向 例：正弦交流电 匀角速 O 恒定均匀 B  求：任意时刻的电动势 解： t N     L V B dl     ( ) BS cos m  n  = BS cost NBS t t dt d N m m  i  sin   sin    O  m  NBS ，转速n ：转/分(r/min)， ( / ) 60 2 rad s n   例：磁通计的原理 B  dt d m i     感应电流 i  G

i=E=-1Φm RR dt 1 0→t 感生电量q=d=R而 .0dΦn=- 1 △①m R qc△Φnm，△Φnm=Rg if,Φn(O)=0,Φm()=Rg:磁通计原理 测量磁场，若线圈面积较小，且线圈平面LB,B=Φ()/S 可测：时变磁场、恒定磁场 对于恒定磁场 B 例：洛仑兹力是否作功？ 洛仑兹力对电荷永远不作功 洛仑兹力是产生动生电动势的非静电力 BX × F=币×B:产生动生电动势 ∫=gi×B:对动生电动势无贡献 1 F=F+f=qm×B+qi×B F外 =q(+)×B=qF×B 7=下+d X F17,Fm·7=0 F、子分别对电荷作功 洛仑兹力不提供能量，它只是转化和传递能量 5

5 dt d R R i i m     1 R 0  t 感生电量 m t m m t t R d R dt dt d R q idt m m               1 1 ( ) 1 0 0 (0) q  m ，m  Rq if，m (0)  0，m (t)  Rq ：磁通计原理 测量磁场，若线圈面积较小，且线圈平面 B，  B  m (t)/ S 可测：时变磁场、恒定磁场 对于恒定磁场 B  例：洛仑兹力是否作功？ 洛仑兹力对电荷永远不作功 洛仑兹力是产生动生电动势的非静电力 B ：产生动生电动势  F  F qv B      u ：对动生电动势无贡献  f qu B      f  v  Fm F f qv B qu B              F外 = =  q v u B    (  ) qV B    V v u      Fm V ，    F V  0 m   F 、 分别对电荷作功  f 洛仑兹力不提供能量，它只是转化和传递能量 q