
量子力学基础 第1节 实物粒子的波粒二象性 光学发展简史 牛 顿:微粒学说,惯性运动的徽粒流 直线传播、反射、折射/ 牛顿环X 惠更斯:波动学说,波动 直线传播、反射、折射/ 干涉、衍射X 几何光学 1801年,杨氏,双缝干涉,光的波长 1815年,菲涅耳,惠更斯菲涅耳原理,直线传播、反射、折射、 干涉、衍射 1817年,杨氏,光是横波,偏振 1865年,麦克斯韦,光是电磁波 19世纪末20世纪初,普朗克,爱因斯坦,光量子假说 h E=hv,P= 入 光的波粒二象性 1924年,德布罗意 几何光学 费马原理: nds=0 波动光学 经典力学 哈密顿原理:δ[Ldt=0 波动力学? 德布罗意假设:一切实物粒子都具有波粒二象性 质量为m、运动速度为V的粒子 E=mc2=hv h 德布罗意关系式 P=mV= 物质波或德布罗意波 非相对论:元=h=h h (Ek= ) P mV √2mE 2m 相对论: =hv1-v2lc P mV moV hc ,(E2=E+c2p2,P=1√E2-E E2-ER E=Eo+Eg,E2=Eo +2EoEg+E hc = 2EoEs+ER ifE>E。,元≈hc E hc h ifE6<<E0,九≈ 2EEg 2mgE
1 量子力学基础 第 1 节 实物粒子的波粒二象性 光学发展简史 牛 顿:微粒学说,惯性运动的微粒流 直线传播、反射、折射 牛顿环 惠更斯:波动学说,波动 直线传播、反射、折射 干涉、衍射 几何光学 1801 年,杨氏,双缝干涉,光的波长 1815 年,菲涅耳,惠更斯-菲涅耳原理,直线传播、反射、折射、 干涉、衍射 1817 年,杨氏,光是横波,偏振 1865 年,麦克斯韦,光是电磁波 19 世纪末 20 世纪初,普朗克,爱因斯坦,光量子假说 E h , h P 光的波粒二象性 1924 年,德布罗意 几何光学 费马原理: nds 0 波动光学 经典力学 哈密顿原理: Ldt 0 波动力学? 德布罗意假设:一切实物粒子都具有波粒二象性 质量为m 、运动速度为V 的粒子 E mc h 2 h P mV 物质波或德布罗意波 非相对论: = , ( ) P h mEk h mV h 2 m P Ek 2 2 相对论: = P h 2 2 0 1 V / c m V h mV h = ,( , ) 2 0 2 E E hc 2 2 2 0 2 E E c P 2 0 1 2 E E c P E E0 Ek , 2 0 2 0 2 E E 2E Ek Ek 2 2E0Ek Ek hc if Ek E0 , Ek hc if Ek E0 , k m Ek h E E hc 2 0 2 0 德布罗意关系式

例:经150V电压加速后,电子的入 解:Ek=eU h 6.63×10-34 = V2mEV2×9.11x10-31×1.6x10-19x150 =1.00261×10-10m≈1A 用相对论公式:1= hc =1.00254×10-10m 2EEg+ER U>104V时,必须使用相对论公式 例:m=0.01kg,V=300m/s的子弹的入 解: V<c,元=h-h=6.63x10-4 =2.21×10-34m P.mV0.01×300 1927年,戴维逊-革末实验 2m=n,n=1,2,3 h h =,2m=n rp=n,L=mh,n=123. 2π 电子显微镜,分辨率Rc1/入 可见光波长:4000~7600A,运动电子的波长:0.1~0.01A 第2节 测不准关系 经典力学:质点,确定的轨道,确定的坐标和动量 微观粒子:波粒二象性,轨道 (x,P)、(y,P)、(:,P)不能同时具有确定的数值 电子 h △x.sinp=元 缝宽△x:电子x坐标的不确定量 只考虑中央亮纹,-Psin中≤P≤Psin中 电子P的不确定量:△P≈Psin中 考虑到次极大:△P≥Psin △r.AP≥△xPsin=2P=h △x·△P.≥i/2,△y-△P.≥h/2,△z·△P≥h/2: 测不准关系式
2 例:经 150V 电压加速后,电子的 解: Ek eU = mEk h 2 2 9.11 10 1.6 10 150 6.63 10 31 19 34 m 10 1.00261 10 1A 用相对论公式: = 2 2E0Ek Ek hc m 10 1.00254 10 U 10 4V 时,必须使用相对论公式 例:m 0.01kg ,V 300m/s的子弹的 解:V c, = = P h mV h m 34 34 2.21 10 0.01 300 6.63 10 1927 年,戴维逊-革末实验 2r n ,n 1,2,3 , P h P h 2r n r , , 2 h rP n L n n 1,2,3 电子显微镜,分辨率 R 1/ 可见光波长: ,运动电子的波长: 4000 ~ 7600A 0.1 ~ 0.01A 第 2 节 测不准关系 经典力学:质点,确定的轨道,确定的坐标和动量 微观粒子:波粒二象性,轨道 (x, Px )、( y, Py )、(z, Pz ) 不能同时具有确定的数值 x P Px Psin P 电子 x y P h x sin 缝宽x :电子 x 坐标的不确定量 只考虑中央亮纹, Psin Px Psin 电子 Px 的不确定量:Px Psin 考虑到次极大:Px Psin x Px xPsin P h x Px / 2 ,y Py / 2,z Pz / 2 :测不准关系式 Py
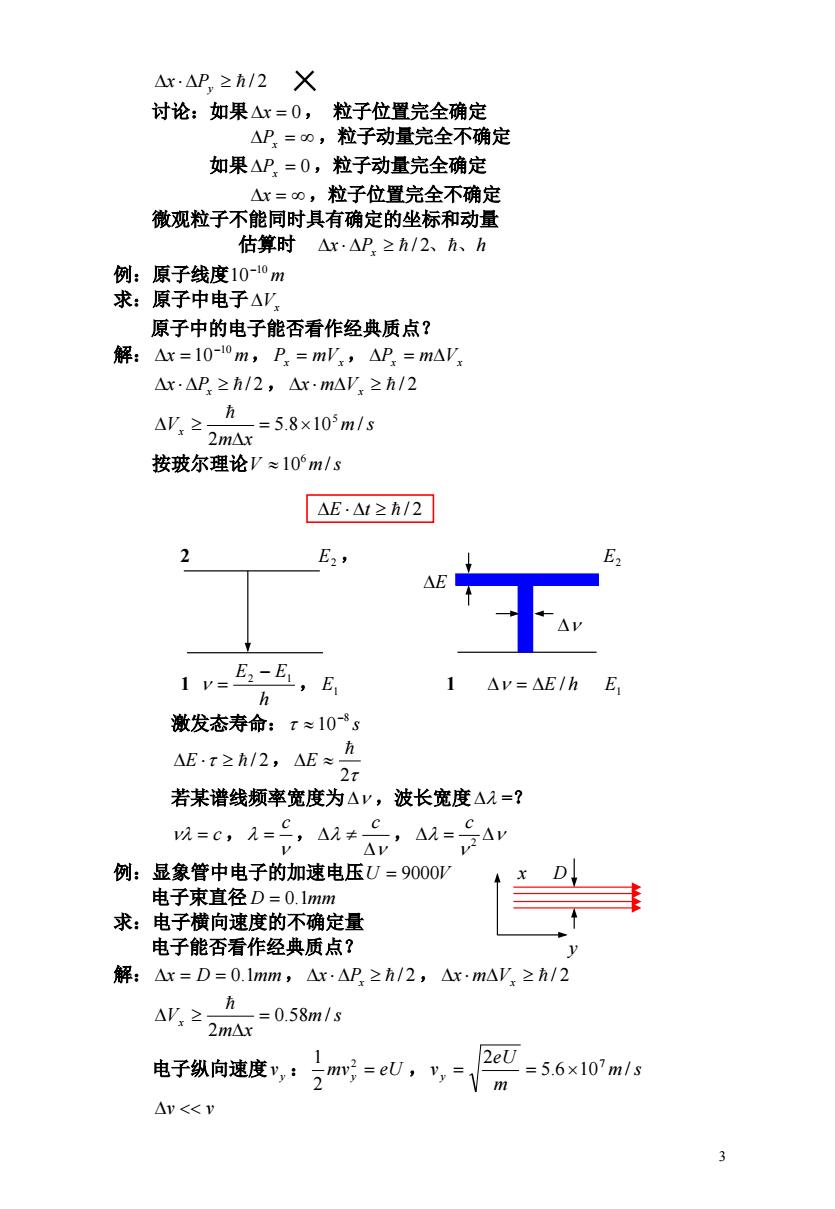
△r·△P≥h/2X 讨论:如果△x=0,粒子位置完全确定 △P=0,粒子动量完全不确定 如果△P.=0,粒子动量完全确定 △x=0,粒子位置完全不确定 微观粒子不能同时具有确定的坐标和动量 估算时△x·△P.≥h/2、i、h 例:原子线度10-10m 求:原子中电子△V 原子中的电子能否看作经典质点? 解:△x=10-1om,P=m'x,△P=mA' △x:△P.2h/2,△x-m△V.2h/2 AV:2 =5.8×103m/s 2m△x 按玻尔理论V≈10°m/s △E·△1≥h/2 2 E2, △ I v=E-,E 1△y=△E/hE h 激发态寿命:x≈10-8s AE:t≥方/2,△E≈克 2t 若某谱线频率宽度为△y,波长宽度△入=? 以=c,1=总AM品,a以=Av 例:显象管中电子的加速电压U=9000W 电子束直径D=0.lmm 求:电子横向速度的不确定量 电子能否看作经典质点? 解:△x=D=0.lmm,△·△P≥i/2,△x·mAV≥方/2 A≥、 =0.58m/s m△x U 电子纵向速度,:2m=eW,V-m =5.6×107m/s △v<<V 3
3 x Py / 2 讨论:如果x 0, 粒子位置完全确定 Px ,粒子动量完全不确定 如果Px 0 ,粒子动量完全确定 x ,粒子位置完全不确定 微观粒子不能同时具有确定的坐标和动量 估算时 x Px / 2、、h 例:原子线度 m 10 10 求:原子中电子Vx 原子中的电子能否看作经典质点? 解:x 10 10 m, Px mVx ,Px mVx x Px / 2 ,x mVx / 2 m s m x Vx 5.8 10 / 2 5 按玻尔理论V 10 m/s 6 E t / 2 2 , E2 E2 E 1 , 1 h E2 E1 E1 E / h E1 激发态寿命: s 8 10 E / 2, 2 E 若某谱线频率宽度为 ,波长宽度 =? c , , , c c 2 c 例:显象管中电子的加速电压U 9000V x D 电子束直径 D 0.1mm 求:电子横向速度的不确定量 电子能否看作经典质点? y 解:x D 0.1mm,x Px / 2 ,x mVx / 2 m s m x Vx 0.58 / 2 电子纵向速度vy : mvy 2 eU , 2 1 m s m eU vy 5.6 10 / 2 7 v v

例:氨氖激光器,元=6328A,△1=10-8A 求:光沿x轴传播时,光子△x 解:Axg≥/2,2=白,=々A 22 -=31.87km 4π△ 例:2=500nm的光沿x轴传播 波长的不确定度(相对误差)△2=10- 求:光子△ 2 解:△2=10-,△x≥ -=0.4m 4π△ 4
4 例:氦氖激光器, , = 6328A A 8 10 求:光沿 x 轴传播时,光子x 解:x Px / 2 , , h Px 2 h Px , = 2 2 h x 4 2 x 31.87km 例: 500nm的光沿 x 轴传播 波长的不确定度(相对误差) 7 10 求:光子x 解: = , = 7 10 4 2 x 0.4m