第3节波函数 薛定谔方程 一、波函数 经典粒子 (F,P) 光子 电磁波波函数E(?,) 实物粒子物质波波函数w(F,) 自由粒子 E=hv,p=h 单色平面波 (x,1)=Acos2x1-克 (x,))=Ae2-》 w(x,t)=W -i2n-》 -2p w(x,t)=wo 方方 三维自由运动,wrG,0=W,ea- 二、波函数的统计解释 电子 波包观点 X 疏密波观点 ●●● 单个电子就具有波动性! 1926年,玻恩:物质波是几率波 dw =v(r,t)'dv d =w(F,tw(F.n)dv, 几率密度:MG,=d形 dv 粒子性:集中的质量、电荷、 不能同时具有确定的坐标、 点粒子 动量,没有确定的运动轨道 波动性:干涉、衍射现象 几率波,波函数不是实在 满足波的迭加原理 的物理量,:几率密度 粒子性:集中的质量、电荷 波动性:微观粒子运动规律的统计性! w(r,t) 电子 有些地方干涉几率加强,有些地方干涉几率相消 电子数较少时,屏上呈现散乱的斑点
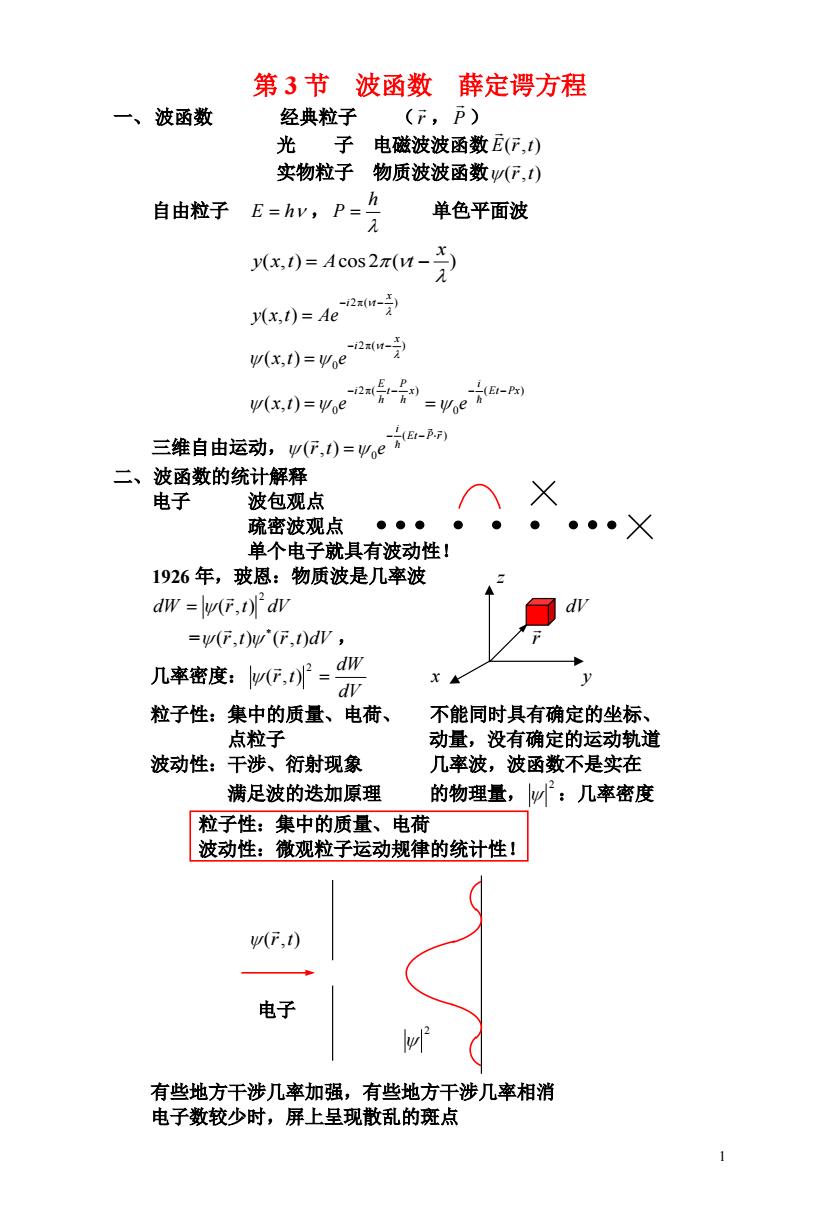
1 第 3 节 波函数 薛定谔方程 一、波函数 经典粒子 (r , ) P 光 子 电磁波波函数 E(r,t) 实物粒子 物质波波函数 (r,t) 自由粒子 E h , 单色平面波 h P ( , ) cos 2 ( ) x y x t A t 2π( ) ( , ) x i t y x t Ae 2π( ) 0 ( , ) x i t x t e ( ) 0 2π( ) 0 ( , ) Et Px i x h P t h E i x t e e 三维自由运动, ( ) 0 ( , ) Et P r i r t e 二、波函数的统计解释 电子 波包观点 疏密波观点 单个电子就具有波动性! 1926 年,玻恩:物质波是几率波 z dW r t dV 2 ( , ) dV = (r,t) (r,t)dV , r 几率密度: dV dW r t 2 ( , ) x y 粒子性:集中的质量、电荷、 不能同时具有确定的坐标、 点粒子 动量,没有确定的运动轨道 波动性:干涉、衍射现象 几率波,波函数不是实在 满足波的迭加原理 的物理量, :几率密度 2 粒子性:集中的质量、电荷 波动性:微观粒子运动规律的统计性! (r,t) 电子 2 有些地方干涉几率加强,有些地方干涉几率相消 电子数较少时,屏上呈现散乱的斑点

电子数足够多时,屏上电子数的分布与几率分布趋于一致 屏上看到的是电子数的分布,反映的是几率分布 光子出现在空间某处的几率密度∝,不再解释为能量密度 三、波函数的标准条件和归一化条件 经典力学:某时刻质点在什么位置?动量是多少?轨迹方程? 量子力学:微观粒子的波函数是什么? 粒子出现在空间各点上的几率是多大? 粒子动量取各种可能数值的几率是多大? 某时刻粒子出现在空间各点上的几率是唯一的、完全确定的 波函数:单值函数 某时刻粒子出现在空间各点上的几率是有限的 波函数:有限的 粒子出现在空间各点上的几率分布及随时间的变化是连续的 波函数:连续的 单值、有限、连续 波函数的标准条件 ∫dw=jldw=l— 归一化条件 “相对几率分布” W(F,t)台Cw(行,),C≠0:复常数 描写的是同一个几率波,粒子的同一个运动状态 n=心0,≠,构造:,0=,0 网aw=Jaw=l (了,):归一化波函数, 京:归一化因子 四、薛定谔方程 质量为m的粒子在势能函数为V(x,y,z,)的外力场中运动 品气祭等兴+w一 薛定谔方程 i=√1:虚数单位 拉普拉斯算符:V-0 ,∂2 及 vu= 8w ow 8w r?+ 0y2+a2 G,)=、 w+Vw 2m 哈密顿算符: 户=-、 v+V,Aw=-Yv+Vy 2m 2m y=户:含时薛定谔方程 8t 2
2 电子数足够多时,屏上电子数的分布与几率分布趋于一致 屏上看到的是电子数的分布,反映的是几率分布 光子出现在空间某处的几率密度 , 不再解释为能量密度 2 E 2 E 三、波函数的标准条件和归一化条件 经典力学:某时刻质点在什么位置?动量是多少?轨迹方程? 量子力学:微观粒子的波函数是什么? 粒子出现在空间各点上的几率是多大? 粒子动量取各种可能数值的几率是多大? 某时刻粒子出现在空间各点上的几率是唯一的、完全确定的 波函数:单值函数 某时刻粒子出现在空间各点上的几率是有限的 波函数:有限的 粒子出现在空间各点上的几率分布及随时间的变化是连续的 波函数:连续的 单值、有限、连续 波函数的标准条件 1 归一化条件 2 dW dV V “相对几率分布” (r,t) , :复常数 C (r,t) C 0 描写的是同一个几率波,粒子的同一个运动状态 ( 0, 1) ,构造: 2 dV A V ( , ) 1 ( , ) r t A r t 1 2 1 2 dV A dV V V (r,t) :归一化波函数, :归一化因子 A 1 四、薛定谔方程 质量为m 的粒子在势能函数为V (x, y,z,t) 的外力场中运动 薛定谔方程 V m x y z r t t i ( ) 2 ( , ) 2 2 2 2 2 2 2 i 1:虚数单位 拉普拉斯算符: 2 2 2 2 2 2 2 x y z 2 2 2 2 2 2 2 x y z V m r t t i 2 2 2 ( , ) 哈密顿算符: V , m H 2 2 2 ˆ V m H 2 2 2 ˆ :含时薛定谔方程 H t i ˆ

五、定态薛定谔方程 粒子势能函数可划分为两大类: (1)势能函数中明显含有时间变量 如:V(x,y,2,)=A(x2+y2+z2)+Bsino (2)势能函数中不明显含有时间变量 如:V(x,y,,)=A(x2+y2+z2)V 如果V不显含1,则H也不显含1,含时薛定谔方程 ⊙业=户w可以用分离变量的方法求解 w(r,t)=w()f(t) wG).@=[iw行川fo dt 访1.01 [yw()】 f dt (F h.0-aw行】=E f dt v(r) Hw(r)=Ew(F) (1) h听0=j0: (2) dt →f)ea yG,=yG)e:定态波函数,定态 iyw(F)=Eyw():定态薛定谔方程 ():定态波函数 定态的性质: (1)定态几率波的振幅()不随时间变化 (2)(行,)=(F):粒子出现在空间各点上的几率密度恒定 (3)粒子能量E是一定值 一维运动(沿x轴),V(x)不显含1,一维定态问题 月=-是d+r闲) 2m dx2 足dP+V(x)w()=Ew) 2m dx d'w(x)2m dx2 E-V()=0 二阶线性常微分方程 3
3 五、定态薛定谔方程 粒子势能函数可划分为两大类: (1)势能函数中明显含有时间变量 如:V (x, y,z,t) A(x y z ) Bsint 2 2 2 (2)势能函数中不明显含有时间变量 如: ( , , , ) ( ) 2 2 2 V x y z t A x y z 如果V 不显含t ,则 Hˆ 也不显含t ,含时薛定谔方程 可以用分离变量的方法求解 H t i ˆ (r,t) (r) f (t) ( )] ( ) ˆ [ ( ) ( ) H r f t dt df t i r ( )] ˆ [ ( ) 1 ( ) 1 H r dt r df t f i [ ˆ ( )] = ( ) 1 ( ) 1 H r dt r df t f i E Hˆ (r) E (r) (1) ( ) : (2) ( ) Ef t dt df t i Et i f t e ( ) ~ :定态波函数,定态 Et i r t r e ( , ) ( ) Hˆ (r) E (r) :定态薛定谔方程 (r) :定态波函数 定态的性质: (1)定态几率波的振幅 (r) 不随时间变化 (2) :粒子出现在空间各点上的几率密度恒定 2 2 (r,t) (r) (3)粒子能量 E 是一定值 一维运动(沿 x 轴),V (x)不显含t ,一维定态问题 ( ) 2 ˆ 2 2 2 V x dx d m H ( ) ( ) ( ) ( ) 2 2 2 2 V x x E x dx d x m [ ( )] ( ) 0 ( ) 2 2 2 2 E V x x m dx d x 二阶线性常微分方程

第4节 一 维无限深势阱 质量为m的粒子,一维运动 势能函数 V(x)1 0 0a d'w(x)2mE dx2 =0,0a,w(x)=0 E:常数,粒子能量 2mE (x)=Asin( 方2x+),0a 数学上讲,n=0,±1,+2… n=0,(x)=0,无意义 n=1及n=-1,4,(x)与y(x)差一常数因子(-1) 4(x)与y1(x)描写粒子的同一个状态 所以只取n=1 A由归一化条件求出 4
4 第 4 节 一维无限深势阱 质量为m 的粒子,一维运动 势能函数 V (x) x x a x a V x 0, 0 0 ( ) ( ) 0 , O ( ) 2 2 2 2 x mE dx d x 0 x a a x x 0, x a ,(x) 0 E :常数,粒子能量 ) , 2 ( ) sin( 2 x mE x A 0 x a 待定常数 A、 E 、 由波函数的标准条件和归一化条件确定 x 0处波函数的连续条件 0 (0) Asin , A 0 ,否则,(x) 0,没有意义 只有sin 0 , 0 ) 2 ( ) sin( 2 x mE x A x a 处波函数的连续条件 ) , 2 0 ( ) sin( 2 a mE a A A 0 ) 0 2 sin( 2 a mE a n , mE 2 2 n 1,2,3 2 , 2 2 2 2ma n E n 1,2,3 n 1, 2 , , 2 2 1 2ma E n 2 2 E2 E1 2 ,En E1 n 2 ,,粒子的定态能量是量子化的 粒子能量为 En 时,波函数为 x x a x a a n x A x n 0 0, sin 0 ( ) 数学上讲,n 0,1,2 n 0,(x) 0,无意义 n 1及n 1, 1 (x) 与 1 (x) 差一常数因子(1) 1 (x) 与 1 (x) 描写粒子的同一个状态 所以只取n 1 A由归一化条件求出
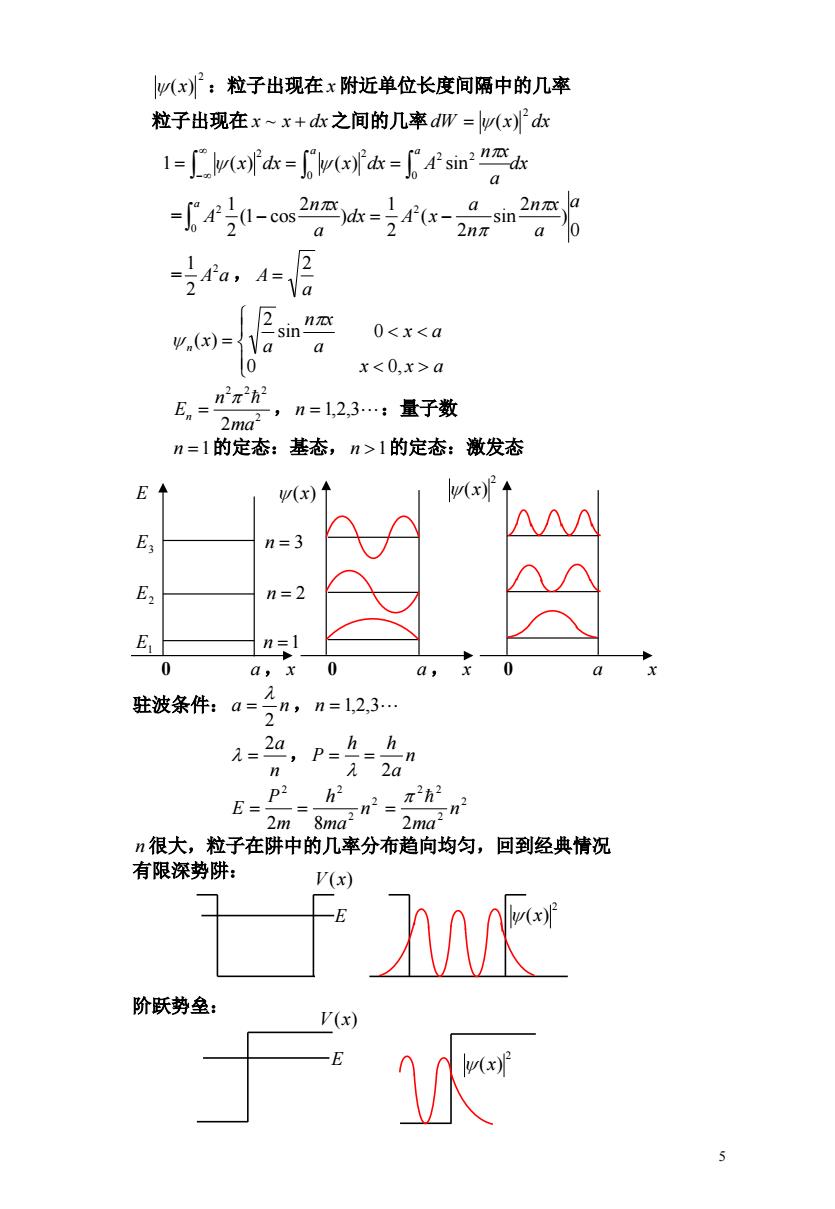
y(x):粒子出现在x附近单位长度间隔中的几率 粒子出现在x~x+dk之间的几率dW=lw(x)d 1=(d=(ofd=sin a -4-as22-4x-n2 nx a 2nπ a a,4层 2 w.(x)=Va sin 0a n2π2h2 E= 2ma2’ n=1,2,3…:量子数 n=1的定态:基态,n>1的定态:激发态 E (x)↑ lw(x)f↑ M E3 n=3 E2 n=2 E n=1 a,x 0 a,x 0 驻波条件:a=二n,n=1,2,3… 2a hh A=44,p=m=n n λ2a p2 h2 E= 2m8.2n2三交h2 n很大,粒子在阱中的几率分布趋向均匀,回到经典情况 有限深势阱: V(x) 阶跃势垒:
5 :粒子出现在 附近单位长度间隔中的几率 2 (x) x 粒子出现在 x ~ x dx 之间的几率dW x dx 2 ( ) dx a n x x dx x dx A a a 0 2 2 0 2 2 1 ( ) ( ) sin = 0 ) 2 sin 2 ( 2 1 ) 2 (1 cos 2 1 2 0 2 a a n x n a dx A x a n x A a = A 2 a , 2 1 a A 2 x x a x a a n x a x n 0 0, sin 0 2 ( ) 2 , :量子数 2 2 2 2ma n En n 1,2,3 n 1的定态:基态,n 1的定态:激发态 E (x) E3 n 3 E2 n 2 E1 n 1 0 a , x 0 a , x 0 a x 驻波条件:a n , 2 n 1,2,3 ,n 2a n a h h P 2 2 2 2 2 2 2 2 2 2 8 2 n ma n ma h m P E n 很大,粒子在阱中的几率分布趋向均匀,回到经典情况 有限深势阱: 阶跃势垒: V (x) V (x) V (x) 2 (x) E 2 (x) E 2 (x)