
第一章质点运动学 (一)确定质点位置的方法、位移、速度、加速度 一、填空、选择题 1.想一想下列两句话是否正确: (1)质点作直线运动,位置矢量的方向一定不变;X (2)质点作圆周运动,位置矢量大小一定不变。X 2.(t)与r(t+△t)为某质点在不同时刻的位置矢量,()与(t+△t)为不同时刻的 速度矢量,试在两个图中分别画出△i,△r,△s及△,△v。 B t+△ 3.一物体在1秒内沿半径R=1m的圆周上从A点运动到B点,如图所示,则物体的平 均速度是: A) (A)大小为2m·s1,方向由A指向B; (B)大小为2m·s1,方向由B指向A; (B)大小为3.14m·9,方向为A点切线方向; (B)大小为3.14m·s,方向为B点切线方向; 4.一质点从P点出发以匀速率1cm·s作顺时针转向的圆周运动,圆半径为1m,如 图。当它走过号国调时走对的路程是受m=小整盒时间平均造度大小为纸“ :方向是C五,及)】 -3 brl=3m m loo's 0 1
第一章 质点运动学 (一 )确 定质点位置的方法、位移、速度、加速度 -、 填空、选择题 1。 想一想下列两句话是否正确 : (1)质 点作直线运动,位置矢量的方向一定不变 ;× (2)质点作圆周运动,位罩矢量大小∵定不变。 Κ 2.i(t)与 氵(t+△ t)为某质点在不同时刻的位置矢量,氵 (t)与 氵(t+△ t)为不同时刻的 速度矢量,试在两个图中分别画出△氵,△ r,△ s及 △氵,△ v。 '犭 s 3.一物体在 1秒内沿半径 R〓 1m的圆周上从 A点运动到 B点 ,如 图所示 ,则 物体的平 均速度是: (A)大小为 2m。 s19方 向由 A指 向 B; (B)大小为 2m。 s~1,方向由 B指 向 A; ·(B)大小为 3.14m° s^1,方 向为 A点切线方向; (B)大小为 3.⒕ m· sJ,方向为 B点切线方向; 酰 当它走畔 盍 蹉 = ‰ 畔 均速度划 叻 揣 咣 =⒋吩Xra^‰ VJ吖 。厉M 刁 古 讠 争 卜 /丨 协 `川 v(r) 亠 ' ⌒ : 、 / X n ε ′ ¢ ) ·1· ‘ 鲤 冫 一一

5.根据瞬时速度矢量ⅴ的定义及其用直角坐标,自然坐标的表示形式,它的大小可表 示为: (BCEG (A) (c (++ ()++, ++, (c[++( 6.某质点的运动方程为x=3t-53+6(SI),则该质点作 (A)匀加速直线运动,加速度沿X轴正方向。 (B)匀加速直线运动,加速度沿X轴负方向。 3-5t2 (C)变加速直线运动,加速度沿X轴正方向。 (D)变加速直线运动,加速度沿X轴负方向。 62 -306 二、计算题 1.已知一质点的运动方程为F=2i+(2-2)j,广、t分别以m和s为单位,求 (1)质点的轨迹方程,并作图。 (2)t=0s和t=2s时刻的位置矢量。 (3)t=0s到t=2s质点的位移△r=?平均速度=? C1)X二26 L2) 60s,广=2m 9=2-62 92-42 -以,7=4))m 个2 惊× (3)a:4-4日 t 2.一质点沿x轴作直线运动,其运动方程为 x=3+5t+62-e(sl) + =5+126-362 则(1)质点在t=0时刻的速度v6=5m/S dx (2)加速度为零时,该质点的速度v=口mS 至=1266 ·2·
△ 5.根据瞬时速度矢量 氵的定义及其用直角坐标,自 然坐标的表示形式,它 的大小可表 示为: ⑴竽,⑶ |甓 | (F)(号芒)2艹 (号芒)2艹 (唁帚)2 (C):帚 , (D)唁青+:芒 +:寻 : ‘⒉, 平均速度 氵=? 钿 s'¢:巧 u 二J+t冫 告^ 丝钅饣乒Ξ二 dz一dt + 业 & + dx一dt G 汪矿II︱Il 刀 Ε lJ 6。 某质点的运动方程为 苓〓3t-5t3+6(SI),则 该质点作 (A)匀加速直线运动,加速度沿X轴 室::∶ 丿告= 3-∫ r舌 (B)匀 · 加速直线运动,加速度沿 X轴 (C)变加速直线运动,加速度沿 X轴 (D)变加速直线运动 ,加速度沿 X轴负 饣 甲 。 凵至± 9 一 ;口 ‘ 二、计算题 1.已知一质点的运动方程为氵=2氵 +(2-t2)j,r、t分别以m和 s为单位,求 , (1)质 点的轨迹方程,并作图。 (2)t=0s和 t〓 2s时刻的位置矢量。 (3)t=0s到 t=2s质点的位移△氵=? 、)Ⅸ二2‘ y二 2-告 ⒉ y÷ ^|— 专1⒉ 加x丿 丿彡C+亻 ·丬b- 窒h× 孓 (2)加 Ⅰ饽 速度为 〖 零 邋 时,该 恧 质点的速度 v=~__止⒎hv3____ (B窿E斫 +扣 +争 ⒈ Δ 一⒉JD饣幻 b菇 ′ !亠 -J亻 ·2·
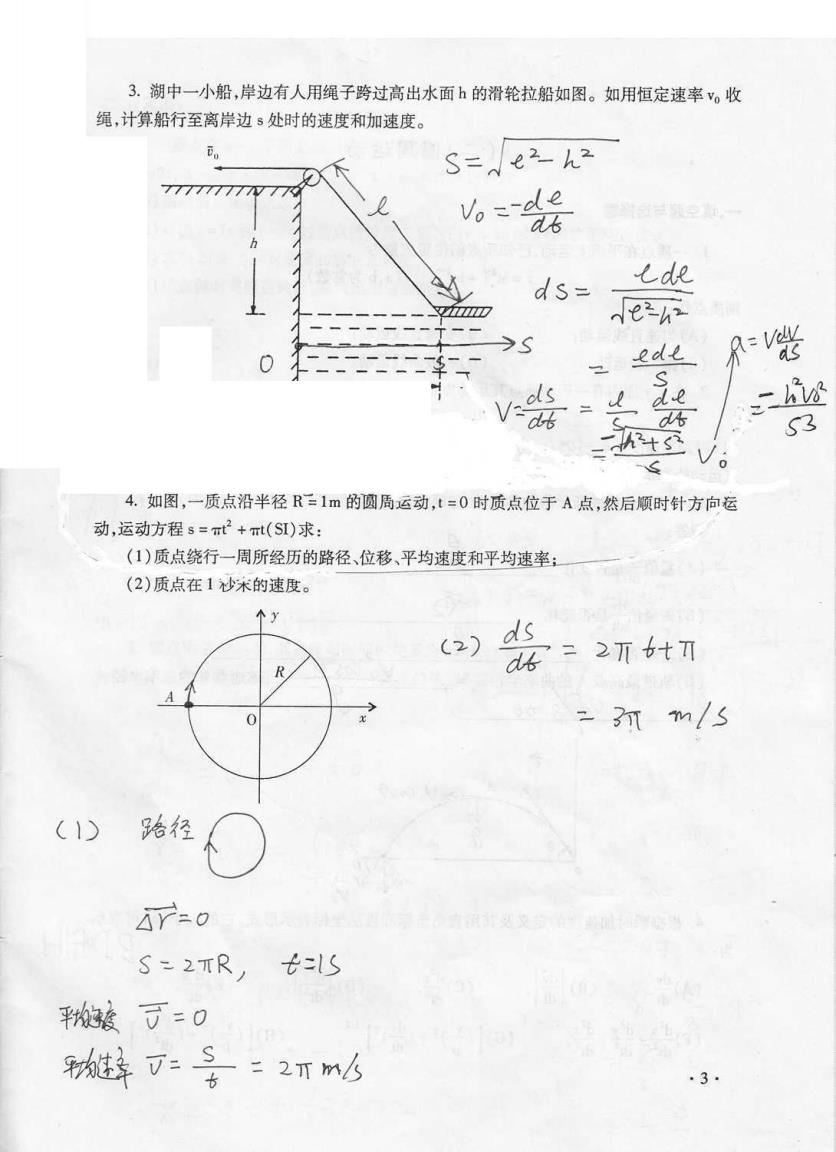
3.湖中一小船,岸边有人用绳子跨过高出水面h的滑轮拉船如图。如用恒定速率。收 绳,计算船行至离岸边3处时的速度和加速度。 S=e22 777777777777 。-c(e 6 ds= 乙de ezh- ede A怅 V- de 53 4.如图,一质点沿半径R=1m的圆周运动,t=0时质点位于A点,然后顺时针方向运 动,运动方程s=πt2+mt(S)求: (1)质点绕行一周所经历的路径、位移、平均速度和平均速率: (2)质点在1秒木的速度。 个y 2) ds R -3ms (1) 治经 Ar=o S=2TR,七=S 平能骏可=0 魅年可:,三2Tm6 ·3
3.湖 中一小船,岸 边有人用绳子跨过高出水面h的滑轮拉船如图。如用恒定速率 vl,收 绳,计算船行至离岸边 s处时的速度和加速度。 召廴 九 一一 ⒉ 呜 s ~~灰ˉ 迓 力 百 II丨 I上 犭。= # ‘ 丿s ∨∷荔疒 '丿 迓 一 s ~ y '逆 I ∶ -≤ 然 Τ 厂 /‘ .吒 局运动,t=0时 质点位于 A点 ,然 后顺时针方 向运 动,运动方程 s〓 "2+付 (sI)求 : ` (1)质阝罕 行丁尸 所经历的蜂径、位移、平均速度和平均速室: 一ˉ (2)质 点在 1秒末的速度。 C冫 9 冫丌 芳寸Π ⒎ 拙 们〃 C丨 D 踣 侄 矽二15 沾一漱 二 勋叶 ∩ 口 扌 一一 ` 胪一 ∴ 幽 铴嶙 ·3· 4.如 图,一质点沿半径 R=1m =之 丌M∠

(二)圆周运动 一、填空题与选择题 1.一质点在平面上运动,已知质点的位置矢量为 f=at21+bt2订 (a,b为常数) 则质点作: (A)匀速直线运动; (B)变速直线运动: (C)抛物线运动; (D)一般曲线运动。 2.在xy面内有一运动质点其运动方程为 =10cos5+10sin5(sI) 则t时刻其速度寸=-Dsn5+5o箕动向加速度a,= 0 ;该质 点运动轨迹是 半经10%69圆 3.一质点作如图所示的抛体运动,忽略空气阻力。 回答: (A)量值密是否变化 是 (®)天量值雪是否变化 (C)a.是否变化 是 (D)轨道最高点A的曲率半径P,= vwo39 ;落地点B的曲率半径P。 V0/9o6 Co>9 9 4.根据瞬时加速度的定义及其用直角坐标和自然坐标表示形式,它的大小1可表示 为: BDGH (A) d (B) d (F) d2+ + d2, (c+(0,([后+9 4
(二 )圆 周运动 一、填空题与选择题 1.一质点在平面上运动,已知质点的位置矢量为 氵=atzi+吖j (a,b为 常数) 则质点作: (A)匀 速直线运动; (C)抛 物线运动; (B)变速直线运动; (D)一般曲线运动。 则t时刻其速庹Ⅱ 苫磊摸 气= 。 ;该 质 点运动轨迹是 o 3.一质点作如图所示的抛体运动,忽 略空气阻力。 回答: (A)量值帑 是否孪化 (B)矢 量值榘是否变化 {:}蜇晷重謇管T瓦瓦菟耳荏Ⅰ∶F亠TΙ≡垂壅耋≡≡≡Ⅰ漾石虿 1的 曲率半径 ρ: -D)轨道最高点 虫 即户 率半径 ρA 叱 c” 、eˉ 根据瞬时加速度的定义及其用直角坐标薪自然坐标表示形式,它 的大小 丨盲丨可表示 匙 为: (A)孥 , (:)|暝|, (C)幸, 〈O常 +::荃 +睾 , (⑴ I(i;)2+(蚩)21 ·4· (Bl丨)》 跻丨}ˉ1丨 (E)常 , (H)I(i;)2∶ (常)21叨 占 nν dt2一 刀

二、计算题: 1.一质点在x-y平面上运动,运动方程为 x=2t, y=19-22 x,y以米计,t以秒计 (1)图示质点运动轨迹: (2)写出t=1s和t=2s时质点的位置矢量,并计算1s到2s间的平均速度; (3)求出2s末的瞬时速度和瞬时加速度, (4)质点何时离原点最近,并求出相应的距离r。 () =5户=4元tl1月 9=19-262 △-2元-6 可=2-6可 9个 =19-空 3) cb =2元-46 器 6225,7=>元-8月 L2)广=26元+9-2t月 6-l57=2元+17月 4r=6)于9-28)2 质X验运式超度时洞微关系为4手致接3 9m处,求质点的运动方程。当t=2s时,质点的位置在哪里? (28)+列 13分日 ∫vh=4t6)h -3726o? =4计34℃ 628时, 6=3 X=12+9+(.=9 x-815-12 C,≥-12 3 X=4t+}6312 m
(、 ) 咕=∶窆 J二 t?-2乇 λ p)'二 冫乇 男 十 ⒄ 一丬 勹 氵 钅二↓‘ ¢=·厉十17歹 二、计算题 : 1.一质点在 x-y平面上运动 ,运动方程为 x〓 2t, y=I9-2t2 x,y以 米计,t以 秒计 (1)图 示质点运动轨迹; (2)写出t=1s和 t〓 厶时质点的位置矢量,并计算 1s到 2s间 的平均速度; (3)求出2s末的瞬时速度和瞬时加速度, (4)质点何时离原点最近,并求出相应的距离r。 舌=灬 ′= 厶一 丫 = ∫甲一菩 γ 纟二以 口 ⒎ 冫写 +丨 l歹 丿涂 J`√ "υ 冫 凵J 犭 ‘ 冖〓艹· 弼 1‘ ⒎ 2.质点沿 X轴运动 ,其速度与时间的关系为 v=4+`m· 、 】 9m处 ,求质点的运动方程。当 t〓 2s时 ,质点的位置在哪里? 瑚 二丿二 4+诌 2 叩 ' 么 ; +\’ `丶 Jy `ι ●ˇ ∧ Ψ ⒉ . /卜 亚 k `一 老 \ 〓 ‘、 ;=勹L0豁 ¢屯 阝⒊亻厅丁「予冫攵°〖h 叫钅二⊥田寸, %⒎ 妒|譬 一丨2 % 亻 5 孕了 疒 τ . 一. 一一 x二 ,/夕二 rL+十 占勹历 = +咕十 犭二3 X= 丨∑十♀弋 ‘ 、二甲 εl△ — 丨℃ γ二 4咕 寸∫钅3-∫ ⒈ 瓦丌= ·万一 印 二务 ⒎ Σ男 十C"冫 t4t,矿 印t 8

3.如图,飞机绕半径R=1km的圆弧在竖直平面内飞行,飞行路程服从s(t)=50+ (m)的规律,飞机飞过最低点A时的速率vA=192m·s',求飞机飞过最低点A时的切向加 速度a,法向加速度a。和总加速度a。 0 V36 张-6=8-6 an 84 4 风=任g a=水 4.y平面内有一运动质点,其运动方程为x=2,y=2t,x,y以m计,t以s计,求质点在t 时刻 (1)速度V=? (2)加速度a=? (3)切向加速度a=? 法向加速度a。=? c) 6 =26 =(26时t写)m5 C2) b (3) V=l mis b .6 n
3.如 图,飞机绕半径 七 1km的 圆弧在竖直平面内飞行,飞行路程服从 s(t)干 sO+′ (m)的规律,飞机飞过最低点 A时的速率 vA〓 192m· s1,求飞机飞过最低点 A时的切向加 速度 %,法向加速度 %和总加速度 盲。 b/二 馐备 二乙∮⒎η臼/s =g‘ 气二钅务争= 贫几干 百 歹:亏 平雏厘黔)¨/s、 动质点 ,其运动方程为 时刻 (0速度氵△? (3)· 切向加速度宙t=? C19 一 ~ 〓一 淑泌一 凵σ 己′9 V=2陌 Ⅱ 步 治 肋 丿〃 ~ ^ 而一 。6· 吡 ⒓陌一 ⒕ 迎 × 亻犭=4乡-/s讧 笏了v旷 二 lγ「 灸:移9`FⅡ/忽tˇ x〓 `,y〓 2t,x,y以 m计,t以 s计 ,求质点在 t (2)加速度 盲〓? 法向加速度 ‰=? 冫七 吒龆|:? c冫 诌芩弋冫歹)% 乙⒎’忒·嘭钅|二 土虏 h/s α咕= 磁

(三)相对运动 一、填空、选择题 1.一质点沿半径为R的园周运动,路程随时间的变化规律为S=bt-2(SD,式中b、 c为大于零的常数,且b>(c) (b-ct)2 (1)质点运动的切向加速度=一C (2)质点经过t=名-足时料N :法向加速度a,R— 2.质点沿半径R作园周运动,运动方程为0=3+2(SI),则t时刻质点法向加速度大 小a,=七R,角加速度B= 4 ,切向加速度大小a=4P 3.某人骑自行车以速率υ向正西方向行驶,遇到由北向南刮的风(设风速大小也为) 则他感到风是从 (C) (A)东北方向吹来, (B)东南方向吹来, (C)西北方向吹来, (D)西南方向吹来。 4.在相对地面静止的坐标系内,A、B两船都以2m·s的速率匀速行驶,A船沿x轴正 向,B船沿y轴正向,今在A船上设置与静止坐标系方向相同的坐标系(x,y方向单位矢用 ,j表示),那么从A船看B船它相对A船的速度(以m·s1为单位)为 (B) (A)2i+2j, (B)-2T+2j, (C)-21-2j, (D)2i-2j 5.楔形物体A的斜面倾角为α,可沿水平方向运动,在斜面上物体B沿斜面以V,相对 斜面下滑时,物体A的速度为V,如图,在固接于地面坐标oxy中B的速度是 矢量式 =正十立 分量式 V=又-V V,= -业Sn2 二、计算题: 1.有架飞机从A处向东飞到B处,然后又向西飞回到A处。已知气流相对于地面的 速率为u,AB之间的距离为1,飞机相对于空气的速率ⅴ保持不变。 1
'阝 ˉ (三 )相 对运动 -、 填空、选择题 1。 一质点沿半径为 R的 园周运动,路程随时间的变化规律为 S=bt-÷ct2(sI),式 中 Ⅱ ∷洳加虫∶迕嚷生。∷ )∷ 旬θ=3+2t2(sI),则 t时刻质忘法向加速度大 小 卩 丁 迪 脚 漱 β [ 胛 脱 度灿 ∵ ← δ 驶,遇 到由北向南刮的风(设风速大小也为v) 则他感到风是从 ,∷ (A)东北方向吹来9 (C)西 北方向吹来9 (B)东 南方向吹来 , (D)西南方向吹来。 (∈ ) 4。 在相对地面静止的坐标系内,A、 B两船都以2m· s^1的 速率匀速行驶 ,A船沿 x轴正 向9B船沿 y轴 正向,今 在 A船上设置与静止坐标系方向相同的坐标系(文 ,y方 向单位矢用 氵,了 表示),那 么从 A船看 β船它相对 A船 的速度(以 m· sl为单位)为 ∴ (5) (A)2i+2了 9 (B)-2i+2i, (0)t2i-2了 , (D)2i-2了 5.楔形物体 A的斜面倾角为 α,可 沿水平方 向运动 ,在斜面上物体 B沿斜面以vr相 对 斜面下滑时,物体 A的速度为 氵,如 图,在 固接于地面坐标 αy中 B的速度是 矢量式 亢地=-Ⅰ吐」L立⊥⊥~~, 分量枣 Ⅴ×=~蹈Ξ耸理L」▲~, 二、计算题: 1。 有架飞机从 A处 向东飞到 B处 9然后又向西飞回到 A处。已知气流相对于地面的 速率为 u,AB之 间的距离为 J9飞 机相对于空气的速率 v保持不变。 ·1· 犭 α

(1)如果u=0(空气静止),试证明来回飞行的时间为,=2斗 (2)如果气流的速度向东,证明来回飞行的时间为1= o 1、 (3)如果气流的速度向北,证明来回飞行的时间为2= to N C3). W-E A (1)显纸 V桃=Ve c-.AB,对8=件M→ 6-2e B94,V对地=V-M5 TV-u 点+名赤两情 2.某物体运动规律为出=-kw1,式中K为大于零的常数,当t=0,初速度为,则速度 dt 与时间的关系是什么? 5e-k 6 db 7:k 2% V=t状 2+Voktx 3.一质点在平面上作曲线运动,其速率v与路程s的关系为v=1+s2(s),写出切向加 速度以路程s表示的表述式。 Qu:%光米v兴 =25(tS3) ·2·
Ⅳ个艹 丨← w (1)如果 u〓 o(空气静止),试证明来回飞行的时间为 tO=竿 (2)如果气流的速度向东,证 明来回飞行的时间为 t1〓 宀 卜勹V (3)I〖 〖F的 罕 F向{9严叩 来回飞行叩 T间饣 饧〓 虍 |郴 刃盱乞∷ ⑴ 钾′- '说 二而 ‘ ∵ ·内吧 ‰扬疒 阡 朗 → 炻,冉 'b/dJ沌 |/~叫 △ 苦F丐专讠 叶缶 :讠毛羊∶军3 -抚 ∫钅 一一 一 ⒉ 与 啪 -k△,2t,式 中Κ为大于零的常数,当 t〓 0,初速度为№,贝 刂速度 `0 法 丿 历 Ⅰ 二一兰k‘ ⒉ ∫ 2y。 k/= 弓廿十扭古’ ^卞 Vo巛乇⒉ 3.一质点在平面上作曲线运动,其速率 v与路程 s的关系为 v=1+s2(豇),写 出切向加 速度以路程 s表示的表述式。 ⒍色=吆聪|=哆管 工膀亍y砻 二2‘ 绀印 ·2·

4.质点沿X轴运动,其加速度和位置的关系是a=2+6x2(sl)。如质点在x=0处的速 度为10m·s1,求质点在任意坐标x处的速度。 人七 二2+6x2 竖d%)=t6x2) g为 62头2x+2x V=Vot4x+4x3=100+4xt4x3 二2 X(+x2)+25 ·3
4.质点沿 X轴运动,其加速度和位置的关系是 aF2+6`(sI)。 如质点在 x=0处 的速 度为 10m· s^l,求质点在任意坐标 x处的速度。 淑歹 咖" /`丿 ζ“廴>浴〓纷十⊥冫卢 y= 亍 9十 JX⒎D灰× 刀 冫 )· 亻xV爿 ^ 丨 ‘ 丬 · ·3·

第二章牛顿运动定律 一、填空题: 1.分别画出物体A、B、C、D的受力图 (1)被水平力F压在墙上保持静止的两个方木块A和B。 (2)被水平力F拉着在水平桌面上一起做匀速运动地木块C和D。 2.如图所示,用一斜同生的力下(与水平成30°角),将一重为G的木块压靠在竖直壁 面上,如果不论用怎样大的力F,都不能使木块向上滑动,则说明木块与壁面间的静摩擦系 数u的大小为 (B) (a≥2 (B)μ≥1/3, (C)u≥23 (D)u≥5 F:G村Gt竖r 30° M>F-G f<mp 3.一质点质量为m,沿半径为R的园周运动,其路程s随时间t变化的规律为 S=b+c(SI) 式中b、c为常数 则质点所受的切向力卫,:2MC七:质点所受的法向力F,= m(6+tt2)2 4.一小车沿半径为R的弯道作园运动,运动方程为日=3+2(SI),则小车所受的向心 力F= (b比饣m。,(设小车的质量为m) 5.质量为m的物体,在力F,=A+Bt(SI)作用下沿x正方向运动(A、B为常数),已知t =0时0A8比H:A8 物体的速度表达式v= 物陈的能帮表陆式(Ab1生吧化 A6+古B63 6.一物体质量M=2kg,在会外力F=(32)了的作角下,从静止出发沿水平x轴作直 .4
第三章 牛顿运动定律 一、填空题: ∶ ∴ ~ I。 分别画出物体 A、 B、 C、 D的受力图 (1)被水平力 F压在墙上保持静止的两个方木块 A和 B。 (2)被水平力 F拉着在水平桌面上⊥起做匀速运动地本块 C和 D∶ j 广 田四 面上,如果不论用怎样太的力 F,都不能使木块向上滑动,则 说明木块与壁面间的静摩擦系 Ⅳ (B)u≥ 1/溽, (D)u≥ √σ 数 u的大小为 (A)u≥ 磅△ '(C)u≥ 2√σ (3) 泸ζ县 'F 3。 一质点质量为 m, 变化 的规律为 S=⒒ +扣 ⑶ 式中 b、 c为常数 ynQ2十 芷 则质点所受的切向力 Ft〓 z阻 C古 ;质点所受的法向力 凡 〓 。 4.一小车沿半径为 R的弯道作园运动 ,运 动方程为 θ=3+2t2(⒏ ),则 小车所受 的向心 Fn=~∫‘咕仫‰ ,(设犭、圭的质堇克乩; 5。 质量为 甲的物体 ,在力 Fx=A十 Bt(sI)作 用下沿 x正方向运动(A、 B为常数),已 知 t 〓0时 x。 =0,vO=09则 任一时劾 乡卩⒍+fζ 伢亡县严F 赫 赢 韫 』 |丁 剔 徘生丝L洲 二 F杆 乜B伊 =`于~华△吾芋 竺工 '苫 /l侈 寸Ⅱ · 一物体质量M=2kg9在否外力f= 物体的位移表达式 x= 灬 6. °4° %卜力 菅 =(3/£t)氵 的榨角 下 ,苁静止出发沿水平 攴插作直