西安电子科技大学：《大学物理》课程习题解答（力学）第7章 刚体力学习题解答

第7章刚体力学习题解答 45 第7章刚体力学习题解答 第七章基本知识小结 7.1.2汽车发动机的转速在12s内由1200 rev/min增加到 3000 rev/min.(1)假设转动是匀加速转动，求角加速度。(2)在此时间内， 1.刚体的质心 发动机转了多少转？ 定义：元=∑m,/m .=∫Fdml∫dm 解：（)B=号=0o0-12002x10=15.7rad/s2 12 求质心方法：对称分析法，分割法，积分法。 (②△8=e=30G-20c2r160=26.39×102ad 2刚体对轴的转动惯量 2B■ 2x15.7 定义：1=∑m, I=∫r2dm 对应的转数=兽=瓷器×102≈420 平行轴定理l。=l+md2 正交轴定理1z=Ik+H 常见刚体的转动惯量：（略） 7.1.3某发动机飞轮在时间间隔t内的角位移为 3.刚体的动量和质心运动定理 0=am+bt3-ct‘(0:rad,t:s）。求t时刻的角速度和角加速度。 p=mm。 ∑F=ma, 4刚体对轴的角动量和转动定理 解：o=竖=a+3br2-4c3B=0=6b1-12ct2 L=lo ∑r=p 7.1.4半径为0.1m的圆盘在铅直平面内转动，在圆盘平面内建 5.刚体的转动动能和重力势能 立o-xy坐标系，原点在轴上，x和y轴沿水平和铅直向上的方向。 E=1o2 E。=m82 边缘上一点A当0时恰好在x轴上，该点的角坐标满足0=1.2+t2 (0rad,ts)。(1t=0时，(2)自t=0开始转45°时，(3)转过90°时，A点 6刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动 的速度和加速度在x和y轴上的投影。 动力学方程： ∑F=ma.∑.=1.B 解：0=架=1.2+21B=架=2.0 (不必考虑惯性力矩) (1=0时，0=1.2，y.=0v,=R=1.2×0.1=0.12m/s 动能：Ek=mm2+1o2 a.=-a=-y,2/R=-0.122/0.1=-0.144m/s2 7刚体的平衡方程 a,=a.=R=2.0x0.1=0.2m/s2 ∑F=0, 对任意轴∑t=0 (2)0=π/4时，由0=1.2t+t2,求得t0.47s,.0=1.2+2t=2.14rad/s

第 7 章刚体力学习题解答 45 第 7 章刚体力学习题解答 A 第七章基本知识小结 ⒈刚体的质心 定义：    rc = mi ri / m rc = rdm / dm     求质心方法：对称分析法，分割法，积分法。 ⒉刚体对轴的转动惯量 定义：   I = mi ri I = r dm 2 2 平行轴定理 Io = Ic+md2 正交轴定理 Iz = Ix+Iy. 常见刚体的转动惯量：（略） ⒊刚体的动量和质心运动定理 = c F = mac p mv     ⒋刚体对轴的角动量和转动定理 L = I  = I ⒌刚体的转动动能和重力势能 k Ep mgyc E = I = 2 2 1  ⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动 动力学方程：  = c  c = c c F ma  I    （不必考虑惯性力矩） 动能： 2 2 1 2 2 1 k c c c E = mv + I  ⒎刚体的平衡方程 F = 0  ， 对任意轴  = 0 7.1.2 汽车发动机的转速在 12s 内由 1200rev/min 增加到 3000rev/min.⑴假设转动是匀加速转动，求角加速度。⑵在此时间内， 发动机转了多少转？ 解：⑴ 2 12 (3000 1200)2 / 60 15.7rad /s t = = = −     ⑵ rad 2 2 15.7 (3000 1200 )(2 / 60) 2 26.39 10 2 2 2 2 0 2  = = =   − −      对应的转数= 10 420 2 2 3.14 26.39 2 =       7.1.3 某发动机飞轮在时间间隔 t 内的角位移为 ( : , : ) 3 4  = at + bt − ct  rad t s 。求 t 时刻的角速度和角加速度。 解： 2 3 2 a 3bt 4ct 6bt 12ct dt d dt d = = + − = = −     7.1.4 半径为 0.1m 的圆盘在铅直平面内转动，在圆盘平面内建 立 o-xy 坐标系，原点在轴上，x 和 y 轴沿水平和铅直向上的方向。 边缘上一点 A 当 t=0 时恰好在 x 轴上，该点的角坐标满足θ=1.2t+t2 (θ:rad,t:s)。⑴t=0 时，⑵自 t=0 开始转 45º时，⑶转过 90º时，A 点 的速度和加速度在 x 和 y 轴上的投影。 y 解： = =1.2 + 2 = = 2.0 dt d dt d t     o x ⑴t=0 时， v v R m s x y  = 1.2, = 0 =  = 1.2 0.1 = 0.12 / 2 2 2 2 2.0 0.1 0.2 / / 0.12 / 0.1 0.144 / a a R m s a a v R m s y x n y = = =  = = − = − = − = −   ⑵θ=π/4 时,由θ=1.2t+t2 ,求得 t=0.47s,∴ω=1.2+2t=2.14rad/s

第7章刚体力学习题解答 46 第7章刚体力学习题解答 yx=-Rc0s45°=-2.14×0.1×V2/2=-0.15m/5 7.1.6收割机拨禾轮上面通常装4到 6个压板，拨禾轮一边旋转，一边随收割 ',=oRsm45°-2.14×0.1×√2/2=0.15m/s 机前进。压板转到下方才发挥作用，一方 面把农作物压向切割器，一方面把切下来 切割器 ax=-BR cos45°-w2Rcos45°=-Rcos45(B+w2) 的作物铺放在收割台上，因此要求压板运 =-0.1×9(2.0+2.142)=-0.465m/s2 动到下方时相对于作物的速度与收割机前进方向相反。 a,=BRsin45°-o2Rsn45°=Rsin45(B-o2) 已知收割机前进速率为1.2m/s,拨禾轮直径1.5m,转速22 rev/min,, =0.1×9(2.0-2.142)=-0.182m/s2 求压板运动到最低点挤压作物的速度。 解：拨禾轮的运动是平面运动，其上任一点的速度等于拨禾轮 (3)0=m/2时，由0=1.2t+t2,求得0.7895s,w=1.2+2t=2.78rad/s 轮心C随收割机前进的平动速度加上拨禾轮绕轮心转动的速度。压 y=-R=-2.78×0.1=-0.278m/sy,=0 板运动到最低点时，其转动速度方向与收割机前进速度方向相反， ax=-R=-2.0×0.1=-0.2m/s2 压板相对地面（即农作物）的速度 a,=-0R=-2.782×0.1=-0.77m/s2 v=V.-R=1.2-2e×2=-0.53m/s 负号表示压板挤压作物的速度方向与收割机前进方向相反。 7.1.5钢制炉门由两个各长1.5m的平行臂 AB和CD支承，以角速率w=10rad/s逆时针转 7.1.7飞机沿水平方向飞行，螺旋桨尖端所在半径为150cm,发 动，求臂与铅直成45°时门中心G的速度和加 动机转速2000 rev/min.(1)桨尖相对于飞机的线速率等于多少？(2)若 速度。 飞机以250km/h的速率飞行，计算桨尖相对地面速度的大小，并定 解：因炉门在铅直面内作平动，所以门中 性说明桨尖的轨迹。 心G的速度、加速度与B点或D点相同，而B、 解：(1)桨尖相对飞机的速度： D两点作匀速圆周运动，因此 V=or=22×1.5=314m/s Vc=VB=oAB=10×1.5=15m/s,方向指向右下方，与水 (②)桨尖相对地面的速度：下=+机地，飞机相对地面的速度与 平方向成45°： a6=aB=o2AB=102×1.5=150m/s2,方向指向右上方， 螺旋桨相对飞机的速度总是垂直的，V机地=恐兴=69.4m/s 与水平方向成45 所以，v=V2+6=5142+69.4年≈321.6m15 显然，桨尖相对地面的运动轨迹为螺旋线

第 7 章刚体力学习题解答 46 第 7 章刚体力学习题解答 · v R m s v R m s y x sin 45 2.14 0.1 2 / 2 0.15 / cos 45 2.14 0.1 2 / 2 0.15 / =  =   = = −  = −   = −   2 2 2 2 2 2 2 2 2 2 2 2 0.1 (2.0 2.14 ) 0.182 / sin 45 sin 45 sin 45 ( ) 0.1 (2.0 2.14 ) 0.465 / cos 45 cos 45 cos 45 ( ) m s a R R R m s a R R R y x =  − = − =  −  =  − = −  + = − = −  −  = −  +         ⑶θ=π/2 时,由θ=1.2t+t2 ,求得 t=0.7895s,ω=1.2+2t=2.78rad/s 2 2 2 2 2.78 0.1 0.77 / 2.0 0.1 0.2 / 2.78 0.1 0.278 / 0 a R m s a R m s v R m s v y x x y = − = −  = − = − = −  = − = − = −  = − =    7.1.5 钢制炉门由两个各长 1.5m 的平行臂 A C AB 和 CD 支承，以角速率ω=10rad/s 逆时针转 动，求臂与铅直成 45º时门中心 G 的速度和加 B D 速度。 解：因炉门在铅直面内作平动，所以门中 G 心 G 的速度、加速度与 B 点或 D 点相同，而 B、 D 两点作匀速圆周运动,因此 v v AB m s G B = = =101.5 =15 / ，方向指向右下方，与水 平方向成 45º； 2 2 2 a a AB 10 1.5 150m/s G = B = =  = ，方向指向右上方， 与水平方向成 45º 7.1.6 收割机拨禾轮上面通常装 4 到 6 个压板，拨禾轮一边旋转，一边随收割 机前进。压板转到下方才发挥作用，一方 面把农作物压向切割器，一方面把切下来 的作物铺放在收割台上，因此要求压板运 动到下方时相对于作物的速度与收割机前进方向相反。 已知收割机前进速率为1.2m/s，拨禾轮直径1.5m，转速22rev/min, 求压板运动到最低点挤压作物的速度。 解：拨禾轮的运动是平面运动，其上任一点的速度等于拨禾轮 轮心 C 随收割机前进的平动速度加上拨禾轮绕轮心转动的速度。压 板运动到最低点时，其转动速度方向与收割机前进速度方向相反， 压板相对地面（即农作物）的速度 v v R m s c 1.2 0.53 / 2 1.5 60 2 22 = − = −  = −   负号表示压板挤压作物的速度方向与收割机前进方向相反。 7.1.7 飞机沿水平方向飞行，螺旋桨尖端所在半径为 150cm，发 动机转速 2000rev/min. ⑴桨尖相对于飞机的线速率等于多少？⑵若 飞机以 250km/h 的速率飞行，计算桨尖相对地面速度的大小，并定 性说明桨尖的轨迹。 解：⑴桨尖相对飞机的速度： v' r 1.5 314m/s 60 2000 2 = =  =    ⑵桨尖相对地面的速度： v v v机地    = '+ ，飞机相对地面的速度与 螺旋桨相对飞机的速度总是垂直的， v 69.4m/s 60 60 250 103 = =   机地 所以， v v' v 314 69.4 321.6m /s 2 2 2 2 = + 机地 = +  显然，桨尖相对地面的运动轨迹为螺旋线

第7章刚体力学习题解答 47 第7章刚体力学习题解答 7.1.8桑塔纳汽车时速为166kmh,车轮滚动半径为0.26m,发 72.3长度为L的匀质杆，令其竖直地立于光滑的桌面上，然后 动机转速与驱动轮转速比为0.909，问发动机转速为每分多少转？ 放开手，由于杆不可能绝对沿铅直方向，故随即到下。求杆子的上 解：设车轮半径为R=0.26m,发动机转速为n,驱动轮转速为 端点运动的轨迹（选定坐标系，并求出轨迹的方程式）。 2,汽车速度为v=166km/h。显然，汽车前进的速度就是驱动轮边缘 解：设杆在o-xy平面内运动。因杆 的线速度，v=2π12=2π1，/0.909，所以： 在运动过程中，只受竖直向上的支承力和 竖直向下的重力的作用，在水平方向不受 n-2-2g=9.24x10ev/h=1.54×103ev/mm 外力作用，∴va=0,aa=0,即质心C无水 平方向的移动，只能逆若y轴作加速直线 运动，直到倒在桌面上。 0 7.2.2在下面两种情况下求直圆锥体的总质量和质心位置。(1)圆 取杆的上端点的坐标为xy,匀质杆的质心在其几何中心，由图 锥体为匀质：(2)密度为h的函数：p=p。(1-hL),po为正常数。 示的任一瞬间的几何关系可知：4x2+y2=L2(x≥0，y≥0) 解：建立图示坐标0-x,据对称性分析， 质心必在x轴上，在x坐标处取一厚为dx 7.3.1(1)用积分法证明：质量为m常为1的匀质细杆对通过中心 的质元dm=p刀k,,a=x/L,r=a/L .dm=p na'x d/L? 且与杆垂直的轴线的转动惯量等于立m：(2)用积分法证明：质量 (1)圆锥体为匀质，即p为常数， 为m半径为R的匀质薄圆盘对通过中心且在盘面内的轴线的转动惯 总质量：m=dm=xk=pmL 量等于：mR2 质心：x。= 证明：(1)取图示坐标，在坐标x处取一线元，dm="水，它 对y轴的转动惯量为：dl=兴x水，三 (2)p=P(1-)=P1-2)=空x 整个细杆对y轴的转动惯量： dx /2 112 总质量：m=∫dm=芒r本=poπaL 1=号∫x2k=号x32=贵（传+的）=立ml2 -12 质心：气告=达=礼 (2)在坐标x处取细杆状质元， dm=0·2√R2-xk=gVR2-x2dk

第 7 章刚体力学习题解答 47 第 7 章刚体力学习题解答 7.1.8 桑塔纳汽车时速为 166km/h，车轮滚动半径为 0.26m，发 动机转速与驱动轮转速比为 0.909, 问发动机转速为每分多少转？ 解：设车轮半径为 R=0.26m，发动机转速为 n1, 驱动轮转速为 n2, 汽车速度为 v=166km/h。显然，汽车前进的速度就是驱动轮边缘 的线速度， v = 2 Rn2 = 2 Rn1 / 0.909 ，所以： 9.24 10 / 1.54 10 /min 4 3 2 3.14 0.26 0.909 166 10 2 0.909 1 3 n rev h rev R v = = =  =       7.2.2 在下面两种情况下求直圆锥体的总质量和质心位置。⑴圆 锥体为匀质；⑵密度为 h 的函数：ρ=ρ0（1-h/L）,ρ0 为正常数。 解：建立图示坐标 o-x,据对称性分析， 质心必在 x 轴上,在 x 坐标处取一厚为 dx o r a x 的质元 dm=ρπr 2 dx，∵r/a=x/L，r=ax/L ∴ dm=ρπa 2 x 2 dx/L2 h ⑴圆锥体为匀质，即ρ为常数， 总质量： m dm x dx a L L L a 2 3 1 0 2 2 2   = = =   质心： x x dx L L a L L a x dx L dm xdm c 4 3 0 3 3 / 3 / 2 3 2 3 2 = =  =   =    ⑵ x L L L x L h 0 (1 ) (1 ) 0 0   =  − =  − = − 总质量：   m = dm = x dx = a L L L a 2 4 0 1 0 3 3 2 0     质心：  = =   = L dm L xdm xc x dx L 0 5 4 4 4 4 7.2.3 长度为 L 的匀质杆，令其竖直地立于光滑的桌面上，然后 放开手，由于杆不可能绝对沿铅直方向，故随即到下。求杆子的上 端点运动的轨迹（选定坐标系，并求出轨迹的方程式）。 解：设杆在 o-xy 平面内运动。因杆 y 在运动过程中，只受竖直向上的支承力和 竖直向下的重力的作用，在水平方向不受 外力作用，∴vcx=0,acx=0，即质心 C 无水 平方向的移动，只能逆着 y 轴作加速直线 运动，直到倒在桌面上。 o x 取杆的上端点的坐标为 x,y，匀质杆的质心在其几何中心，由图 示的任一瞬间的几何关系可知：4x2+y2=L2 (x≥0,y≥0) 7.3.1 ⑴用积分法证明：质量为 m 常为 l 的匀质细杆对通过中心 且与杆垂直的轴线的转动惯量等于 2 12 1 ml ；⑵用积分法证明：质量 为 m 半径为 R 的匀质薄圆盘对通过中心且在盘面内的轴线的转动惯 量等于 2 4 1 mR 证明：⑴取图示坐标，在坐标 x 处取一线元， dm dx l m = ，它 对 y 轴的转动惯量为： dI x dx l m 2 = ， 整个细杆对 y 轴的转动惯量： 2 12 1 3 8 8 / 2 / 2 3 3 / 2 / 2 2 | ( ) 3 3 I x dx x ml l l l l m l l m l l l m = = − = + = −  ⑵在坐标 x 处取细杆状质元， dm R x dx R x dx R m R m 2 2 2 2 2 = 2  2 − = 2 −   L x y -l/2 dx l/2 x x R θ

第7章刚体力学习题解答 48 第7章刚体力学习题解答 它对x轴的转动惯量： 平行轴定理 dI=dm(2R-x)=dm(Rx)=(R-x)2 dx L1=立m,12+m,()2=m,l2, I,=m,r2+m,(+r)2 整个圆盘对x轴的转动惯量：1=条j(R2-x2)水 I=m,l2+m,r2+m,(1+r)2 =}×4.9×0.922+×24.5×0.082+24.5(0.92+0.08)2 =26kgm2 为了能求出积分，作如下变换：x=Rcos0,dr=-Rsin0d0 7.3.3在质量为M,半径为R的匀质圆盘上挖出半径为r的两个 (R2-x2)32=(R2-R2cos203/2=(R2sn2032=R3sin30 圆孔，圆孔中心在半径R的中点，求剩余部分对过大圆盘中心且与 盘面垂直的轴线的转动惯量。 解：大圆盘对过圆盘中心。且与盘面 代入上式：1=0jR3sm0-Rsn0d0)=2gjsn0ad0 垂直的轴线（以下简称o轴）的转动惯量 为1=士MR2.由于对称放置，两个小圆 据三角函数公式：sn'0=1-cos2 2 -cos0=1+cos20 2 盘对。轴的转动惯量相等，设为'，圆盘 ∴.sin40=(=g22)2=1(1-2cos20+cos220) 质量的面密度a=MWπR2,根据平行轴定理， =41-2cos20+±g0)=(号-2cos20+cos40) =2+(axr'=+Mr 设挖去两个小圆盘后，剩余部分对。轴的转动惯量为I” I=(-2cos20+cos40)do =1-2I=MR2-答-h2=MR2-r2-2r1R2) do-codco0 =9 7.3.5一转动系统的转动惯量为1=8.0kgm2,转速为o=41.9rad/s, (号π-sn206+sn406)=mR 两制动闸瓦对轮的压力都为392N,闸瓦与轮缘间的摩擦系数为μ =0.4,轮半径为=0.4m,问从开始制动到静止需多长时间？ 7.3.2图示实验用的摆，1=0.92m=0.08m,m=4.9kgm=24.5kg 解：由转动定理： 近似认为圆形部分为匀质圆盘，长杆部分为匀质细杆。求对过悬点 t=Iβ，B=；=204204=15.68ad/s 且与盘面垂直的轴线的转动惯量。 80 解：摆对0轴的转动惯量1等于杆对0轴的转动 制动过程可视为匀减速转动，B=△0/△1 惯量1，加上圆盘对o轴的转动惯量L,即=l+l,.根据 南瓦

第 7 章刚体力学习题解答 48 第 7 章刚体力学习题解答 它对 x 轴的转动惯量： dI dm R x dm R x R x dx R m 2 2 3/ 2 3 2 2 2 3 2 2 2 1 12 1 = (2 − ) = ( − ) = 2 ( − )  整个圆盘对 x 轴的转动惯量：  − = − R R R m I R x dx 2 2 3/ 2 3 2 2 ( )  为了能求出积分，作如下变换： x = Rcos, dx = −Rsin d    2 2 3/ 2 2 2 2 3/ 2 2 2 3/ 2 3 3 (R − x ) = (R − R cos ) = (R sin ) = R sin 代入上式：   = − =          0 4 3 2 0 3 3 3 2 sin ( sin ) sin 2 I 2 R R d d mR R m 据三角函数公式： 2 1 cos 2 , cos 2 1 cos 2 sin 2 2     + = − = (1 2cos 2 ) ( 2cos 2 cos 4 ) sin ( ) (1 2cos 2 cos 2 ) 2 1 2 3 4 1 2 1 cos 4 4 1 2 4 2 1 2 4 1 cos 2         = − + = − +  = = − + + − 2 4 1 8 0 1 2 0 3 6 0 8 1 0 0 2 3 6 2 1 2 3 4 1 3 2 ( sin 2 | sin 4 | ) cos2 2 cos4 4 ( 2cos2 cos4 ) 2 2 2 mR d d d I d mR mR mR = − + =       = − + = − +                        7.3.2 图示实验用的摆，l=0.92m,r=0.08m,ml=4.9kg,mr=24.5kg, 近似认为圆形部分为匀质圆盘，长杆部分为匀质细杆。求对过悬点 且与盘面垂直的轴线的转动惯量。 o 解：摆对 o 轴的转动惯量 I 等于杆对 o 轴的转动 惯量 Il 加上圆盘对 o 轴的转动惯量 Ir，即 I=Il+Ir.根据 平行轴定理 2 2 2 2 2 1 3 1 2 2 2 2 1 3 1 2 2 2 1 2 3 2 1 2 2 12 1 26 4.9 0.92 24.5 0.08 24.5(0.92 0.08) ( ) ( ) ( ) , kgm I m l m r m l r I m r m l r I m l m m l l r r r r r l l l l l = =   +   + + = + + + = + + = + = 7.3.3 在质量为 M，半径为 R 的匀质圆盘上挖出半径为 r 的两个 圆孔，圆孔中心在半径 R 的中点，求剩余部分对过大圆盘中心且与 盘面垂直的轴线的转动惯量。 解：大圆盘对过圆盘中心 o 且与盘面 R 垂直的轴线（以下简称 o 轴）的转动惯量 r r 为 2 2 I = 1 MR .由于对称放置，两个小圆 盘对 o 轴的转动惯量相等，设为 I’，圆盘 质量的面密度σ=M/πR 2，根据平行轴定理， 2 4 1 2 2 2 2 2 2 2 1 2 4 I' ( r )r ( r )( ) M r R R M r =  +  = + 设挖去两个小圆盘后，剩余部分对 o 轴的转动惯量为 I” " 2 ' ( 2 / ) 2 2 4 2 2 2 1 2 2 1 2 1 2 4 I I I MR Mr M R r r R R M r = − = − − = − − 7.3.5 一转动系统的转动惯量为 I=8.0kgm2，转速为ω=41.9rad/s， 两制动闸瓦对轮的压力都为 392N，闸瓦与轮缘间的摩擦系数为μ =0.4，轮半径为 r=0.4m，问从开始制动到静止需多长时间？ 解：由转动定理： I rad s I , 15.68 / 8.0 2 0.4 392 0.4 = = = =        制动过程可视为匀减速转动，  =  / t o l r 闸瓦 闸瓦

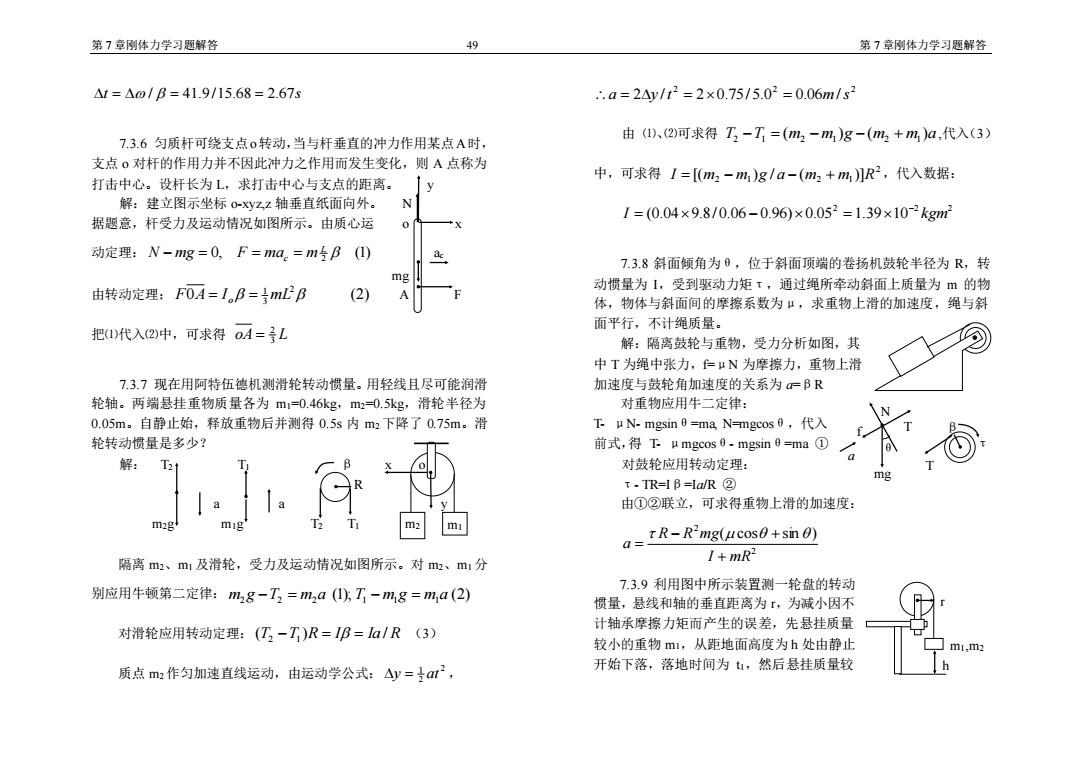
第7章刚体力学习题解答 49 第7章刚体力学习题解答 △1=△0/B=41.9115.68=2.67s .a=2△y/t2=2×0.75/5.02=0.06m/s2 7.3.6匀质杆可绕支点0转动，当与杆垂直的冲力作用某点A时， 由(1)、（②）可求得T3-T1=(m2-m)g-(m2+m)a,代入(3) 支点0对杆的作用力并不因此冲力之作用而发生变化，则A点称为 打击中心。设杆长为L,求打击中心与支点的距离。 中，可求得I=[m2-m)g/a-(m2+m)R2,代入数据： 解：建立图示坐标0-xyzz轴垂直纸面向外。 N I=(0.04×9.8/0.06-0.96×0.052=1.39×10-2kgm 据题意，杆受力及运动情况如图所示。由质心运 动定理：N-mg=0,F=ma。=m号B(1) 7.3.8斜面倾角为9，位于斜面顶端的卷扬机鼓轮半径为R,转 由转动定理：F0A=I。B=mLB 动惯量为1，受到驱动力矩τ，通过绳所牵动斜面上质量为m的物 体，物体与斜面间的摩擦系数为μ，求重物上滑的加速度，绳与斜 面平行，不计绳质量。 把1)代入(2)中，可求得oA=L 解：隔离鼓轮与重物，受力分析如图，其 中T为绳中张力，=μN为摩擦力，重物上滑 7.3.7现在用阿特伍德机测滑轮转动惯量。用轻线且尽可能润滑 加速度与鼓轮角加速度的关系为=BR 轮轴。两端悬挂重物质量各为m1=0.46kg,m2=0.5kg,滑轮半径为 对重物应用牛二定律： 0.05m。自静止始，释放重物后并测得0.5s内m2下降了0.75m。滑 下uN.-mgsin9=ma,N-ngcos9，f代入 轮转动惯量是多少？ 前式，得下u mgcos9.mgsin9=ma① 解： 对鼓轮应用转动定理： mg t.TR=B=la/R② 由①②联立，可求得重物上滑的加速度： m TR-R'mg(ucos0+smn 0) Q=. 隔离m2、m1及滑轮，受力及运动情况如图所示。对m2、m1分 1+mR2 别应用牛顿第二定律：m28-T3=m2a(,T-m8=ma(2) 7.3.9利用图中所示装置测一轮盘的转动 惯量，悬线和轴的垂直距离为，为减小因不 计轴承摩擦力矩而产生的误差，先悬挂质量 对滑轮应用转动定理：(T-T)R=IB=1a/R(3) 较小的重物m,从距地面高度为h处由静止 m1,m2 质点m2作匀加速直线运动，由运动学公式：△y=2, 开始下落，落地时间为1，然后悬挂质量较

第 7 章刚体力学习题解答 49 第 7 章刚体力学习题解答 t =  /  = 41.9 /15.68 = 2.67s 7.3.6 匀质杆可绕支点o转动，当与杆垂直的冲力作用某点A时， 支点 o 对杆的作用力并不因此冲力之作用而发生变化，则 A 点称为 打击中心。设杆长为 L，求打击中心与支点的距离。 y 解：建立图示坐标 o-xyz,z 轴垂直纸面向外。 N 据题意，杆受力及运动情况如图所示。由质心运 o x 动定理： 0, (1) 2  L N − mg = F = mac = m ac 由转动定理； 0 (2) 2 3 1 F A = I o = mL  A F 把⑴代入⑵中，可求得 oA L3 2 = 7.3.7 现在用阿特伍德机测滑轮转动惯量。用轻线且尽可能润滑 轮轴。两端悬挂重物质量各为 m1=0.46kg，m2=0.5kg，滑轮半径为 0.05m。自静止始，释放重物后并测得 0.5s 内 m2 下降了 0.75m。滑 轮转动惯量是多少？ 解： T2 T1 β x o R a a y m2g m1g T2 T1 隔离 m2、m1 及滑轮，受力及运动情况如图所示。对 m2、m1 分 别应用牛顿第二定律： (1); (2) m2 g −T2 = m2a T1 − m1g = m1a 对滑轮应用转动定理： (T2 −T1 )R = I = Ia / R （3） 质点 m2 作匀加速直线运动，由运动学公式： 2 2 1 y = at ， 2 2 2 a = 2y /t = 20.75/ 5.0 = 0.06m/s 由 ⑴、⑵可求得 T2 −T1 = (m2 − m1 )g − (m2 + m1 )a ,代入（3） 中，可求得 2 2 1 2 1 I = [(m − m )g / a − (m + m )]R ，代入数据： 2 2 2 I (0.04 9.8/ 0.06 0.96) 0.05 1.39 10 kgm − =  −  =  7.3.8 斜面倾角为θ，位于斜面顶端的卷扬机鼓轮半径为 R，转 动惯量为 I，受到驱动力矩τ，通过绳所牵动斜面上质量为 m 的物 体，物体与斜面间的摩擦系数为μ，求重物上滑的加速度，绳与斜 面平行，不计绳质量。 解：隔离鼓轮与重物，受力分析如图，其 中 T 为绳中张力，f=μN 为摩擦力，重物上滑 加速度与鼓轮角加速度的关系为 a=βR 对重物应用牛二定律： T- μN- mgsinθ=ma, N=mgcosθ，代入 前式，得 T- μmgcosθ- mgsinθ=ma ① 对鼓轮应用转动定理： τ- TR=Iβ=Ia/R ② 由①②联立，可求得重物上滑的加速度： 2 2 ( cos sin ) I mR R R mg a + − + =     7.3.9 利用图中所示装置测一轮盘的转动 惯量，悬线和轴的垂直距离为 r，为减小因不 计轴承摩擦力矩而产生的误差，先悬挂质量 较小的重物 m1，从距地面高度为 h 处由静止 开始下落，落地时间为 t1，然后悬挂质量较 mg m2 m1 mg T N f a θ T τ β m1,m2 h r

第7章刚体力学习题解答 50 第7章刚体力学习题解答 大的重物m2,同样自高度h处下落，所需时间为口，根据这些数据 7.4.1扇形装置如图，可绕光滑的铅直轴线o转动，其转动惯量 确定轮盘的转动惯量，近似认为两种情况下摩擦力矩相等。 为1装置的一端有槽，槽内有弹簧，槽的中心轴线与转轴垂直距离为 解：隔离轮盘与重物，受力及运动情况如图 「。在槽内装有一小球，质量为m,开始时用细线固定，使弹簧处于 示：Tr为摩擦力矩，T为绳中张力，a=Br 压缩状态。现在燃火柴烧断细线，小球以速度弹出。求转动装置 对轮盘应用转动定理： 的反冲角速度。在弹射过程中，由小球和转动装置构成的系统动能 Tr-t,=I邛，Tr-tr=邛2，两式相减，得： 守恒否？总机械能守恒否？为什么？ mg 解：取小球、转动装置构成的物体系为研究对象。在弹射过程 中，物体系相对竖直轴0未受外力距作用，故物体系对转轴0的角 (T3-T)r=I(B2-B),I=(T3-T)r《B2-B)① 动量守恒，规定顺时方向为正，有 对重物应用牛顿二定律： I-。=0∴.0=。/I m8-T=m141=mB,m2g-T3=m2a2=m2B2，两式相减， 在弹射过程中，物体系动能不 守恒，因弹力做正功使动能增加： 可得：T3-T=(m2-m1)g-(m2B2-mB),代入①中，可得： 总机械能守恒，因为只有保守内力（弹力）做功。 I=(m2-m)gr-(m2B2-m,B)r2]《B2-B)② 7.4.2质量为297kg,长为1.0m的匀质等截面细杆可绕水平光 滑的轴线0转动，最初杆静止于铅直方向。一弹片质量为10g,以水 由运动学公式：h=a42=a2422,.a1=2h/1, 平速度200m/s射出并嵌入杆的下端，和杆一起运动，求杆的最大摆 2h 角9. ,B= 3， 将角加速度代入②中，得： 解：将子弹、杆构成的物体系作为研究对象， rt It. 整个过程可分为两个阶段研究： I= (m-m)g-(m:普-m÷r 第一阶段，子弹与杆发生完全非弹性碰撞， 获得共同的角速度0，此过程时间极短，可认 为杆原地未动。由于在此过程中，外力矩为零， m v =m,-m82-2m2m,122-m,1 因此角动量守恒，mvl=ml2o+}M2o=(m+号M)2o 2h42-122)122) =m,-m)g2122-2hr2(m,42-m42 ..=(mry=(oo=2.0rad /s 2ht2-t22) 第二阶段，子弹与杆以共同的初角速度0摆动到最大角度日， 由于在此过程中，只有重力做功，所以物体系的机械能守恒，物体

第 7 章刚体力学习题解答 50 第 7 章刚体力学习题解答 大的重物 m2，同样自高度 h 处下落，所需时间为 t2，根据这些数据 确定轮盘的转动惯量，近似认为两种情况下摩擦力矩相等。 解：隔离轮盘与重物，受力及运动情况如图 示：τf 为摩擦力矩，T 为绳中张力，a=βr 对轮盘应用转动定理： 1 1 T r  I − f = ， 2  2 T r  I − f = ，两式相减，得： (T2 −T1 )r = I( 2 − 1 ), I = (T2 −T1 )r/( 2 − 1 ) ① 对重物应用牛顿二定律： 1 1 1 1 1 1 2 2 2 2 2 2 m g −T = m a = m r ,m g −T = m a = m r ，两式相减， 可得： ( ) ( ) 2 1 2 1 m2 2 m11 T −T = m − m g − r − ，代入①中，可得： I = [(m2 − m1 )gr − (m2 2 − m11 )r 2 ]/( 2 − 1 ) ② 由运动学公式： , 2 / , 2 1 1 2 2 2 2 1 2 2 1 1 1 h = a t = a t a = h t 2 2 2 2 1 2 1 2 2 2 , 2 , 2 rt h rt h t h a =  =  = ，将角加速度代入②中，得： 2 ( ) ( ) 2 ( ) 2 ( )/( ) ( ) 2 ( / / ) ( ) ( ) 2 2 2 1 2 1 2 2 2 1 2 2 2 2 1 2 2 1 2 2 2 1 2 2 2 1 2 1 1 2 2 2 2 2 2 1 2 2 2 2 1 2 2 1 2 2 1 2 2 2 1 2 2 h t t m m gr t t hr m t m t h t t t t m m gr hr m t m t m m gr m m r I rt h rt h rt h rt h − − − − = − − − − = − − − − = 7.4.1 扇形装置如图，可绕光滑的铅直轴线 o 转动，其转动惯量 为 I.装置的一端有槽，槽内有弹簧，槽的中心轴线与转轴垂直距离为 r。在槽内装有一小球，质量为 m，开始时用细线固定，使弹簧处于 压缩状态。现在燃火柴烧断细线，小球以速度 v0 弹出。求转动装置 的反冲角速度。在弹射过程中，由小球和转动装置构成的系统动能 守恒否？总机械能守恒否？为什么？ 解：取小球、转动装置构成的物体系为研究对象。在弹射过程 中，物体系相对竖直轴 o 未受外力距作用，故物体系对转轴 o 的角 动量守恒，规定顺时方向为正，有 v0 I rmv 0 rmv / I  − 0 =  = 0 r 在弹射过程中，物体系动能不 o I 守恒，因弹力做正功使动能增加； 总机械能守恒，因为只有保守内力（弹力）做功。 7.4.2 质量为 2.97kg，长为 1.0m 的匀质等截面细杆可绕水平光 滑的轴线 o 转动，最初杆静止于铅直方向。一弹片质量为 10g，以水 平速度 200m/s 射出并嵌入杆的下端，和杆一起运动，求杆的最大摆 角θ. o 解：将子弹、杆构成的物体系作为研究对象， 整个过程可分为两个阶段研究： 第一阶段，子弹与杆发生完全非弹性碰撞， θ 获得共同的角速度ω，此过程时间极短，可认 为杆原地未动。由于在此过程中，外力矩为零， m v 因此角动量守恒，    2 3 2 1 3 2 1 mvl = ml + Ml = (m + M )l rad s m M l mv 2.0 / (0.01 2.97 / 3) 1.0 0.01 200 ( / 3)  = = = +    + 第二阶段，子弹与杆以共同的初角速度ω摆动到最大角度θ， 由于在此过程中，只有重力做功，所以物体系的机械能守恒，物体 m l M T T mg a β τf r

第7章刚体力学习题解答 51 第7章刚体力学习题解答 系原来的动能等于重力势能的增量： 由机械能守恒： (m+M)@2=mgl(1-cos0)+Mg(1-cos0) mghc =lo',mgmho2,o =3gIh ÷c0s0=1-g20a2=1-82*0.8635 (2m+)g 上端点到达地面时的线速度： 0=30°34' v=oh=3gh=√3×9.8×10=17.2m/s 7.4.3一质量为m1,速度为v1的子弹沿水平面击中并嵌入一质 量为m=99m1,长度为L的棒的端点，速度v1与棒垂直，棒原来静 7.5.2用四根质量各为m长度各为1的匀质细杆制成正方形框 止于光滑的水平面上，子弹击中棒后共同运动，求棒和子弹绕垂直 架，可绕其中一边的中点在竖直平面内转动，支点0是光滑的。最 与平面的轴的角速度等于多少？ 初，框架处于静止且AB边沿竖直方向，释放后向下摆动，求当AB 解：以地为参考系，把子弹和棒看作 A m2,L 边达到水平时，框架质心的线速度及框架作用于支点的压力N, 一个物体系，棒嵌入子弹后作平面运动， 解：先求出正方形框架对支点0的转动惯量： 1 vI C O 可视为随质心C的平动和绕质心C的转 m 1。=I.+4m号)2=1.+ml2 动，绕质心C转动的角速度即为所求。 Ep=0 1.=4(位ml2+m)=÷ml21。=子ml2 据质心定义： %=C0m+m2=C0+C4100=L 北==gg=I B A m2CA’m2 CA’99-2CA 设AB边达到水平位置时，框架的角速 度为0，据机械能守恒定律：4mg号=1。o2=(仔ml2)o2 CA=99L/200=0.495L,C0=0.5L-0.495L=0.005L ∴o=,.=o=g 据角动量守恒：m,,CA=(m,CA2+文m2L2+m2CO)@ AB边在水平位置时，框架所受到的向上的支撑力N和向下的 my×0.495L=m1(0.4952+t×99+99×0.0052)L20 重力W的作用线均通过支点o,对0轴的力矩为零，据转动定理， 框架的角加速度为零，∴.a=w2/2=6g/7,方向向上。规定向上方向 0.495y,=(0.4952+99/12+99×0.0052)Lo 为正，对框架应用质心运动定理： 0=0.0581/L N-4mg=4ma。=4m号g∴.N=4mg(1+9)=7号mg 7.5.110m高的烟肉因底部损坏而倒下来，求其上端到达地面时 据牛顿第三定律，支点受到的压力，大小等于N,方向向下。 的线速度，设倾倒时，底部未移动，可近似认为烟囱为匀质杆。 解：设烟肉质量为m,高为h,质心高度hc=h/2,对转轴的转 7.5.3由长为1，质量为m的匀质细杆组成正方形框架，其中一 动惯量I=古mh+m()2=}mh,倒在地面上时的角速度为w 角连于水平光滑转轴O,转轴与框架所在平面垂直，最初，对角线

第 7 章刚体力学习题解答 51 第 7 章刚体力学习题解答 系原来的动能等于重力势能的增量： cos 1 1 0.8635 ( ) (1 cos ) (1 cos ) (2 0.01 2.97) 9.8 2 (0.01 2.97 / 3) 1.0 2.0 (2 ) ( / 3) 2 2 2 3 1 2 1 2  = − = −  + = − + −  +  +   + +      m M g m M l mgl Mg l m M l θ=30º34’ 7.4.3 一质量为 m1，速度为 v1 的子弹沿水平面击中并嵌入一质 量为 m2=99m1，长度为 L 的棒的端点，速度 v1 与棒垂直，棒原来静 止于光滑的水平面上，子弹击中棒后共同运动，求棒和子弹绕垂直 与平面的轴的角速度等于多少？ 解：以地为参考系，把子弹和棒看作 一个物体系，棒嵌入子弹后作平面运动， 可视为随质心 C 的平动和绕质心 C 的转 动，绕质心 C 转动的角速度即为所求。 据质心定义: CA L CA CO CA m m m CA CO m m 99 2 100 , , 2 1 2 2 1 = + = + = ， CA = 99L / 200 = 0.495L, CO = 0.5L − 0.495L = 0.005L 据角动量守恒： ( ) 2 2 2 12 2 2 1 m1 v1CA = m1CA + m L + m CO v L v L m v L m L 0.058 / 0.495 (0.495 99 /12 99 0.005 ) 0.495 (0.495 99 99 0.005 ) 1 2 2 1 2 2 12 2 1 1 1 1 = = + +   = +  +     7.5.1 10m 高的烟囱因底部损坏而倒下来，求其上端到达地面时 的线速度，设倾倒时，底部未移动，可近似认为烟囱为匀质杆。 解：设烟囱质量为 m，高为 h，质心高度 hC=h/2，对转轴的转 动惯量 2 3 2 1 2 2 12 1 I mh m( ) mh h = + = ，倒在地面上时的角速度为ω 由机械能守恒： mgh I mg mh g h h C , , 3 / 2 2 3 1 2 1 2 2 2 1 =   =    = 上端点到达地面时的线速度： v =h = 3gh = 39.810 =17.2m/s 7.5.2 用四根质量各为 m 长度各为 l 的匀质细杆制成正方形框 架，可绕其中一边的中点在竖直平面内转动，支点 o 是光滑的。最 初，框架处于静止且 AB 边沿竖直方向，释放后向下摆动，求当 AB 边达到水平时，框架质心的线速度 vc及框架作用于支点的压力 N. 解：先求出正方形框架对支点 o 的转动惯量： 2 3 2 7 3 4 4 2 12 1 2 2 2 4( ) 4 ( ) 2 I ml m ml I ml I I m I ml o l c c l o c = + =  = = + = + Ep=0 设 AB 边达到水平位置时，框架的角速 度为ω，据机械能守恒定律： 2 2 3 7 2 2 1 2 1 2 4mg l = I o = ( ml ) v l gl l c g 7 3 2 1 7 12  = , =  = AB 边在水平位置时，框架所受到的向上的支撑力 N 和向下的 重力 W 的作用线均通过支点 o，对 o 轴的力矩为零，据转动定理， 框架的角加速度为零，∴ac=ω2 l/2=6g/7，方向向上。规定向上方向 为正，对框架应用质心运动定理： N mg mac m g N mg mg 7 3 7 6 7 6 − 4 = 4 = 4  = 4 (1+ ) = 7 据牛顿第三定律，支点受到的压力，大小等于 N，方向向下。 7.5.3 由长为 l，质量为 m 的匀质细杆组成正方形框架，其中一 角连于水平光滑转轴 O，转轴与框架所在平面垂直，最初，对角线 A B B A C O o A m2,L v1 m1

第7章刚体力学习题解答 52 第7章刚体力学习题解答 OP处于水平，然后从静止开始向下自由摆动，求OP对角线与水平 成45°时P点的速度，并求此时框架对支点的作用力。 7.5.4质量为m长为1的匀质杆，其B端放在桌上，A端用手支 解：先求出框架对O轴的转动惯量：据平行轴定理， 住，使杆成水平。突然释放A端，在此瞬时，求：(1)杆质心的加速 I=Le+4m0C2=4(位mP+m1)+4m方2=9ml2 度，(2)杆B端所受的力。 解：(1)以支点B为转轴，应用转动 B 设对角线OP转过45°后框架的角速度为 0,且势能为零，由机械能守恒： 定理：mg5=mlB∴B=是，质 4mg(sin 45)=lo2,2mgl =mlo2 心加速度a。=B5=是g,方向向下。 o2=等，0=，y,=021=2层g (2)设杆B端受的力为N,对杆应用 质心运动定理：N,=0, 设支点O对框架的作用力为N,由定轴转动定理：T=IB, B=mgm451巨3g 13g3√2 Ns-mg =-m dc,Ns=m(g-dd)=mg/4 10m12/3 a,=B252108 ∴.N=mg4,方向向上。 质心的法向加速度a,=020C=6g.=6g 7.5.5下面是匀质圆柱体在水平地面上作无滑滚动的几种情况， 求地面对圆柱体的静摩擦力 51√25√2 (1)沿园柱体上缘作用一水平拉力F,柱体作加速滚动。 (2)水平拉力F通过圆柱体中心轴线，柱体作加速滚动。 在i方向应用质心运动定理：N,-4 ng cos45°=41an, (3)不受任何主动力的拉动或推动，柱体作匀速滚动。 N =2v2mg+4m. =25+245 (④)在主动力偶矩τ的驱动下加速滚动，设柱体半径为R。 W2 22g )mg= 解：规定前进方向和顺时针方向为正方向。 5×21 5 N 假设静摩擦力方向向后，其余受力情况如图所 F(1) 所示。对每种情况，都可以根据质心定理、绕 在t方向应用质心运动定理：N,+4mgsn45°=4ma. F(2) 质心轴的转动定理和只滚不滑条件，建立三个 N=ng-22mg=停-25mg=-号万mg 方程求解。 mg (1)F-f=ma,(F+fR=mR-B,a BR N=√N,2+N。=√是+密mg=6.32mg,设与-方向夹 可求得∫=·F3,负号说明静摩擦力方向与假设方向相反，应向前。 角为8,0=arctg|Nn/N,=actg5.5=79.7 (2)F-f=mae,fR=÷mRB,a。=R

第 7 章刚体力学习题解答 52 第 7 章刚体力学习题解答 OP 处于水平，然后从静止开始向下自由摆动，求 OP 对角线与水平 成 45°时 P 点的速度，并求此时框架对支点的作用力。 解：先求出框架对 O 轴的转动惯量：据平行轴定理， 2 3 2 10 2 2 1 4 2 1 12 2 1 I I 4mOC 4( ml m l ) 4m( l) ml = C + = + + = 设对角线 OP 转过 45°后框架的角速度为 ω，且势能为零，由机械能守恒： 2 2 3 2 5 2 1 2 4mg( l sin 45) = I , 2mgl = ml  v l gl l p g l g 5 3 5 6 5 2 6  = , = , = 2 = 2 设支点 O 对框架的作用力为 N，由定轴转动定理：τ= Iβ， g l g a l g ml mg l I 10 3 2 5 2 3 2 , 5 3 10 / 3 4 sin 45 / 2 2 = = = =  = =     质心的法向加速度 5 2 6 5 2 2 6 l g l g an = OC =  = 在 n ˆ 方向应用质心运动定理： Nn mg 45 4man − 4 cos  = ， mg mg g Nn mg m 2 5 22 ) 5 2 24 2 (2 2 5 2 6 2 2 4 =  = +  = + 在  ˆ 方向应用质心运动定理： N mg 45 4ma + 4 sin  = N m g mg mg 2mg 5 4 2) 2 5 6 2 2 2 ( 10 3  = 4  − = − = − N N Nn mg 6.32mg 25 2 22 25 32 2 2 2 = + = + =   ，设与- ˆ 方向夹 角为θ， = arctg | N / N |= arctg5.5 = 79.7  n  7.5.4 质量为 m 长为 l 的匀质杆，其 B 端放在桌上，A 端用手支 住，使杆成水平。突然释放 A 端，在此瞬时，求：⑴杆质心的加速 度，⑵杆 B 端所受的力。 解：⑴以支点 B 为转轴，应用转动 B A 定理： l l g mg ml 2 2 3 3 1 2 =    = ，质 心加速度 a g l c 4 3 2 =  = ，方向向下。 x ⑵设杆 B 端受的力为 N，对杆应用 y 质心运动定理：Ny=0， Nx - mg = - m ac , Nx = m(g – ac) = mg/4 ∴ N = mg/4，方向向上。 7.5.5 下面是匀质圆柱体在水平地面上作无滑滚动的几种情况， 求地面对圆柱体的静摩擦力 f. ⑴沿圆柱体上缘作用一水平拉力 F,柱体作加速滚动。 ⑵水平拉力 F 通过圆柱体中心轴线，柱体作加速滚动。 ⑶不受任何主动力的拉动或推动，柱体作匀速滚动。 ⑷在主动力偶矩τ的驱动下加速滚动，设柱体半径为 R。 解：规定前进方向和顺时针方向为正方向。 假设静摩擦力方向向后，其余受力情况如图所 所示。对每种情况，都可以根据质心定理、绕 质心轴的转动定理和只滚不滑条件，建立三个 方程求解。 ⑴ F − f = mac ,(F + f )R = mR ,ac = R 2 2 1 可求得 f = - F/3,负号说明静摩擦力方向与假设方向相反，应向前。 ⑵ F − f = mac , fR = mR ,ac = R 2 2 1 O P C n τ 4mg N mg f N F(1) C F(2)

第7章刚体力学习题解答 53 第7章刚体力学习题解答 可求得f=F3,正号说明静摩擦力方向与假设方向相同，向后。 将N、代入(5)中，有 (3)ae=0,f=0 F-4(M+M2)g-号M,a=Ma.a=E-w+“l 3M+M2 (④)-f=ma,t+R=mRB,a。=R,求得f=-最 负号说明静摩擦力方向与假设方向相反，应向前。 7.5.7在水平桌面上放置一质量为m的线轴，内径为b,外径为 R其绕中心轴转动惯量为mR3,线轴和地面之间的静摩擦系数为μ。 7.5.6板的质量为M,受水平力F 线轴受一水平拉力F,如图所示。 的作用，沿水平面运动，板与平面间的 (1)使线轴在桌面上保持无滑滚动之F最大值是多少？ 摩擦系数为u,在板上放一半径为R质 (2)若F和水平方向成9角，试证，cos9>bR时，线轴向前滚： 量为M的实心圆柱，此圆柱只滚动不 cos0,a>0,B<0,即线轴向前滚： 2a=RB与(6)联立，可求得，ac=a/3,代入(1)中，6=aM/3:

第 7 章刚体力学习题解答 53 第 7 章刚体力学习题解答 可求得 f = F/3,正号说明静摩擦力方向与假设方向相同，向后。 ⑶ ac = 0 , f = 0 ⑷ − f = mac , + fR = mR ,ac = R 2 2 1 ,求得 R f 3 2 = − 负号说明静摩擦力方向与假设方向相反，应向前。 7.5.6 板的质量为 M，受水平力 F R 的作用，沿水平面运动，板与平面间的 M2 F 摩擦系数为μ.在板上放一半径为 R 质 量为 M2 的实心圆柱，此圆柱只滚动不 滑动。求板的加速度。 解：隔离圆柱，其受力及运动情况如图 β 所示，其中 ac为质心对地的加速度，β为相 对质心的角加速度，f2、N2 分别为板施加给 W2 ac 圆柱的静摩擦力和压力。 f2 由质心定理： (1), (2) f 2 = M2ac N2 = M2 g N2 对质心应用转动定理： (3) 2 2 2 1 f 2R = M R  N1 隔离木板，其受力及运动情况如图所示， f2 F 其中 a 为板对地的加速度，f1、N1 分别为水平 f1=μN1 Mg 面施加给板的滑动摩擦力和压力。 N2 a 应用牛顿第二定律（或质心定理）： (4) N1 = N2 + Mg (5) F − N1 − f 2 = Ma 圆柱在木板上只滚不滑的条件是：a = ac +βR (6) (圆柱与板接触点对地的加速度等于质心加速度加上绕质心转动的加 速度，即 ac+βR，它必须等于木板对地的加速度 a,才能只滚不滑) 将（2）代入（4）求得：N1=(M+M2)g；由（1）（3）可解得， 2ac=Rβ 与（6）联立，可求得，ac=a/3, 代入（1）中，f2 = a M2 /3； 将 N1、f2 代入（5）中，有 2 2 3 3[ ( ) ] 3 2 1 2 ( ) M M F M M g F M M g M a Ma a + − + − + − =  =   7.5.7 在水平桌面上放置一质量为 m 的线轴，内径为 b，外径为 R,其绕中心轴转动惯量为 mR2 /3,线轴和地面之间的静摩擦系数为μ。 线轴受一水平拉力 F,如图所示。 ⑴使线轴在桌面上保持无滑滚动之 F 最大值是多少？ ⑵若 F 和水平方向成θ角，试证，cosθ＞b/R 时，线轴向前滚； cosθ＜b/R 时，线轴向后滚动。 y 解：可将（1）看作（2）的特殊 F 情况。建立图示坐标，z 轴垂直纸面 C b R x 向外，为角量的正方向。根据静摩擦 θ 力的性质，可知其方向与 F 水平分量 f 方向相反。设线轴质心的加速度为 a， 绕质心的角加速度为β。 由质心定理： F cos − f = ma (1) N = mg − F sin  (2) 由转动定理： (3) 2 3 1 Fb − fR = mR  只滚不滑：a+βR=0 (4) 由⑴,⑶,⑷联立，可求得： (cos ) , ( cos ) , (3 cos ) 4 4 3 4 3 a    f b R  R F R b mR F R b m F = − = − = + ⑴ F 为水平拉力时，即 f b R mg R F cos =1, = 4 (3 + )   F mg b R R +   3 4  . ⑵ 若 cos  , a  0 ,   0 R b ，即线轴向前滚；

第7章刚体力学习题解答 54 第7章刚体力学习题解答 若cos00,即线轴向后滚。 由(2)解得：N,=W(1-a/D+F/1 将N2代入(1)中得：N,=Wa/1-Fh/I 7.5.9一质量为m,半径为r的均质实心小球沿圆弧形导轨自静止 开始无滑滚下，园弧形导轨在铅直面内，半径为R。最初，小球质 令F=O,即得到无拖车时前后轮的支持力N,和N'。显然，有 心与圆环中心同高度。求小球运动到最低点时的速率以及它作用于 拖车时，前轮支持力减小，后轮支持力增大。 导轨的正压力。 解：设小球运动到最低点时，其质心速 7.6.3电梯高22m,其质心在中央，悬线亦 度为，绕质心转动的角速度为0，由机械 在中央。另有负载50×10kg,其重心离电梯中 能守恒，有mg(R-r）=mm2+(传mr2)o2 垂线相距0.5m。问(1)当电梯匀速上升时，光滑 导轨对电梯的作用力，不计摩擦（电梯仅在四角 N 只滚不滑条件：w=h,代入上式，可求得v=√品(R-r)g 处受导轨作用力)：(2)当电梯以加速度0.05m/s2 Mg 上升时，力如何？ 在最低点应用质心运动定理：N-mg=w2《R-r) 解：(1)以o为轴，据力矩平衡条件：N1=mgb “N=mg+v2《R+r】=m(g+石g)=2号mg,作用于导轨的 N=mgb/1=50×10×9.8×0.5/2.2=1.114×103N 正压力与此等大，方向向下。 (2)设电梯的加速度为α，以电梯为参考系，负载除受重力外，还 受惯性力作用*=ma,方向向下，据力矩平衡条件：N1=m(g+a)b 7.6.1汽车在水平路面上匀速行驶，后面牵引旅行拖车，假设拖 车仅对汽车施以水平向后的拉力F汽车重W,其重心与后轴垂直距离 为a,前后轴距离为1，h表示力F与地面的距离。问汽车前后论所受 N=m(g+a)b/1=50×10(9.8+0.05)0.5/2.2=1.119×103N 地面支持力与无拖车时有无区别？试计算之。 解：隔离汽车，受力 情况如图所示（摩擦力没 有画出，因与此题无关)。 在竖直方向应用力平 G 衡方程：N,+N2=W() 以前轮为支点，由力矩平衡方程，N,I=W(I-a)+Fh(2)

第 7 章刚体力学习题解答 54 第 7 章刚体力学习题解答 若 cos  , a  0 ,   0 R b ，即线轴向后滚。 7.5.9 一质量为 m,半径为r 的均质实心小球沿圆弧形导轨自静止 开始无滑滚下，圆弧形导轨在铅直面内，半径为 R。最初，小球质 心与圆环中心同高度。求小球运动到最低点时的速率以及它作用于 导轨的正压力。 解：设小球运动到最低点时，其质心速 度为 v，绕质心转动的角速度为ω，由机械 能守恒，有 2 2 5 2 2 2 1 2 1 mg(R − r) = mv + ( mr ) 只滚不滑条件：ω=v/r,代入上式，可求得 v (R r)g 10 7 = − 在最低点应用质心运动定理： /( ) 2 N − mg = mv R − r N m g v R r m g g mg 7 3 10 2 7  = [ + /( + )] = ( + ) = 2 ，作用于导轨的 正压力与此等大，方向向下。 7.6.1 汽车在水平路面上匀速行驶，后面牵引旅行拖车，假设拖 车仅对汽车施以水平向后的拉力 F.汽车重 W,其重心与后轴垂直距离 为 a,前后轴距离为 l，h 表示力 F 与地面的距离。问汽车前后论所受 地面支持力与无拖车时有无区别？试计算之。 解：隔离汽车，受力 情况如图所示（摩擦力没 C F 有画出，因与此题无关）。 h 在竖直方向应用力平 N1 W a N2 衡方程： (1) N1 + N2 =W 以前轮为支点，由力矩平衡方程， ( ) (2) N2 l =W l − a + Fh 由（2）解得： N W(1 a /l) Fh/l 2 = − + 将 N2 代入(1)中得： N Wa /l Fh/l 1 = − 令 F=0，即得到无拖车时前后轮的支持力 N1’和 N2’。显然，有 拖车时，前轮支持力减小，后轮支持力增大。 7.6.3 电梯高 2.2m，其质心在中央，悬线亦 在中央。另有负载 50×10kg，其重心离电梯中 垂线相距 0.5m。问⑴当电梯匀速上升时，光滑 导轨对电梯的作用力，不计摩擦（电梯仅在四角 处受导轨作用力）；⑵当电梯以加速度 0.05m/s2 上升时，力如何？ 解：⑴以 o 为轴,据力矩平衡条件： Nl = mgb N mgb l N 3 = / = 50109.80.5/ 2.2 =1.11410 ⑵设电梯的加速度为 a，以电梯为参考系，负载除受重力外，还 受惯性力作用 f*=ma,方向向下, 据力矩平衡条件： Nl = m(g + a)b N m g a b l N 3 = ( + ) / = 5010(9.8 + 0.05)0.5/ 2.2 =1.11910 l l Mg mg N o