
第一章 光的干涉(Interference of light) §1光源的发光特性 一.光源 光源的最基本发光单元是分子、原子 能级跃迁辐射 波列 E1 v= (E2-E1)/h E1 波列长L=re 1.普通光源:自发辐射 独立(不同 原子发的光) 独立(同一原子先后发的光)
第一章 光的干涉( ) § 光源的发光特性 一 光源 光源的最基本发光单元是分子、原子 = (E2 -E1 )/h E1 E2 能级跃迁辐射 波列 波列长L= c 普通光源:自发辐射 独立(不同 原子发的光) · · 独立(同一原子先后发的光)

2.激光光源:受激辐射 振动方向,传播方向) 1 二.光的相干性 1.两列光波的叠加(只讨论电振动) 2 E-光矢量,令E,=E2,0,=0=0 P: E,=E。C0s(ot+p) E2=Ez cos(@t+2) E=E +E2=E cos(@t+) E=Ea+En+2EE0c0s△p △0=92-P1
激光光源:受激辐射 = (E2 -E1 )/h E1 E2 完全一样(频率,位相, 振动方向,传播方向) 二 光的相干性 两列光波的叠加 只讨论电振动 E −光矢量, 令 E1 = E2 , 1 =2 = p · · · 1 2 r1 r2 cos( ) 1 = 10 +1 E E t cos( ) 2 = 20 + 2 E E t P: 1 2 E0 E10 E20 cos( ) E = E1 + E2 = E0 t + = + + 2 10 20 cos 2 20 2 10 2 E0 E E E E = 2 −1

.I=I1+I2+2VII2c0s△p ·非相干光源cos△p=0 I=I1+I2一非相干叠加 ·完全相干光源cos△p=cos△o ▲相长干涉(明)△p=±2kπ, I=Imax=11+I2+2VT1l2(k=0,1,2,3…) ▲相消干涉(暗)△p=±(2k+1)π, I=1mim=11+12-2VI1L2(k=0,1,2,3…) 2.条纹衬比度(对比度,反衬度) ,Imax一Imin Imax Imin
2 cos I = I1 + I 2 + I1 I 2 • 非相干光源 cos = 0 非相干叠加 • 完全相干光源 cos = cos ▲相长干涉(明) = 2k , max 1 2 2 1 2 I = I = I + I + I I ▲相消干涉(暗) = (2k +1) , min 1 2 2 1 2 I = I = I + I − I I max min max min I I I I V + − = 条纹衬比度(对比度,反衬度)
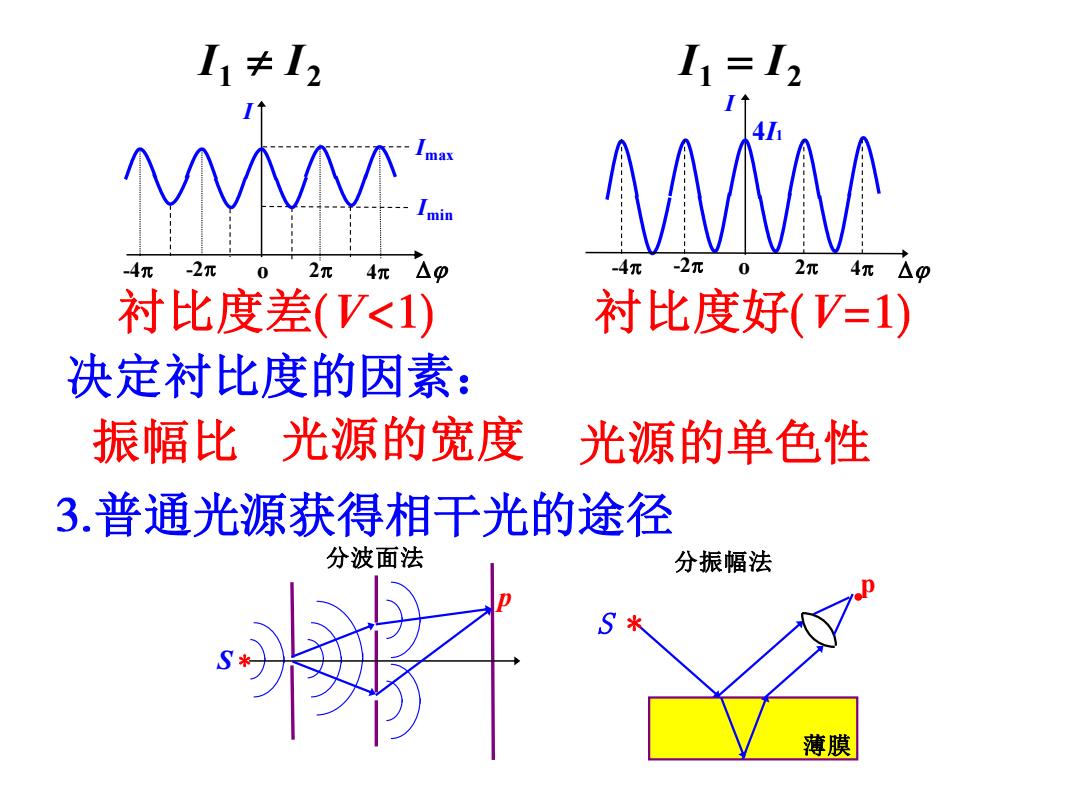
I1≠I2 11=12 I↑ A -4元-2元02π4π△9 4 2元4元m 衬比度差(V<1) 衬比度好(V=1) 决定衬比度的因素: 振幅比光源的宽度 光源的单色性 3.普通光源获得相干光的途径 分波面法 分振幅法 薄膜
1 2 I I 1 2 I = I I -4 -2 o 2 4 4I1 普通光源获得相干光的途径 p S * 分波面法 分振幅法 · p 薄膜 S * 衬比度差 衬比度好 振幅比 决定衬比度的因素: 光源的宽度 光源的单色性 I Imax Imin -4 -2 o 2 4
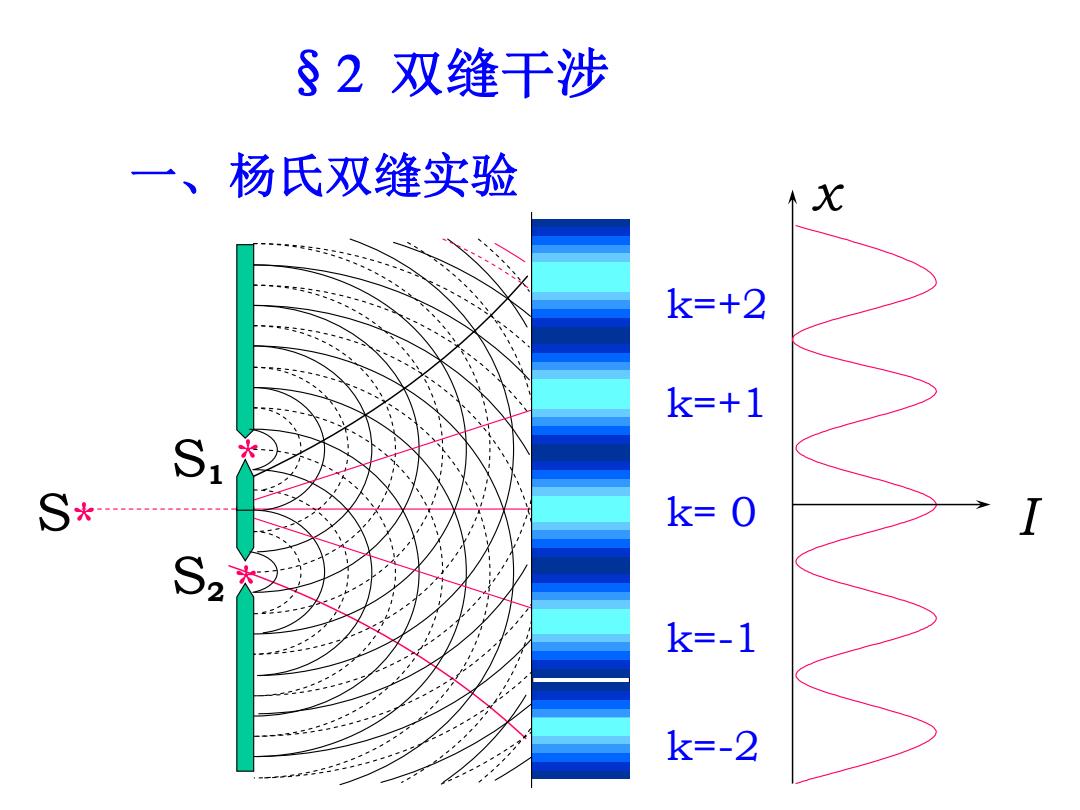
§2双缝干涉 一、 杨氏双缝实验 S* 02
S1 S2 S* * * x k=+1 k=-2 k=+2 k= 0 k=-1 I 一、杨氏双缝实验 § 双缝干涉

二.双缝干涉 单色光入射 d>>λ,D>>d(d~10-4m,D~m 波程差:6=h-h≈dsin0≈dg0=d. 相位差: 4ps 2 2 D 明纹6=±2,x士k=±k 2,k=0,1,2 d 暗纹 D 6=(2k+2x+)=主2k+D
二 双缝干涉 x 0x I x p r1 · r2 xx D d o 单色光入射, 波程差: Dx = r − r d sin d tg = d 2 1 相位差: = 2 明纹 = , = , k = 0,1,2… dD k x k k 暗纹 2 , (2 1) 2 (2 1) (2 1) dD = k + x k+ = k +

条纹间距△x= D 条纹特点: (1)一系列平行的明暗相间的条纹; (2)0不太大时条纹等间距; (3)中间级次低: 某条纹级次=该条纹相应的(-)/入 明纹:±k,k=1,2,3…(整数级) 暗纹:(2+1)/2 (半整数级) (4)△xc元
条纹间距 d D x = 一系列平行的明暗相间的条纹; 中间级次低; 明纹 , 整数级 暗纹 半整数级 x 条纹特点: 不太大时条纹等间距; 某条纹级次 该条纹相应的
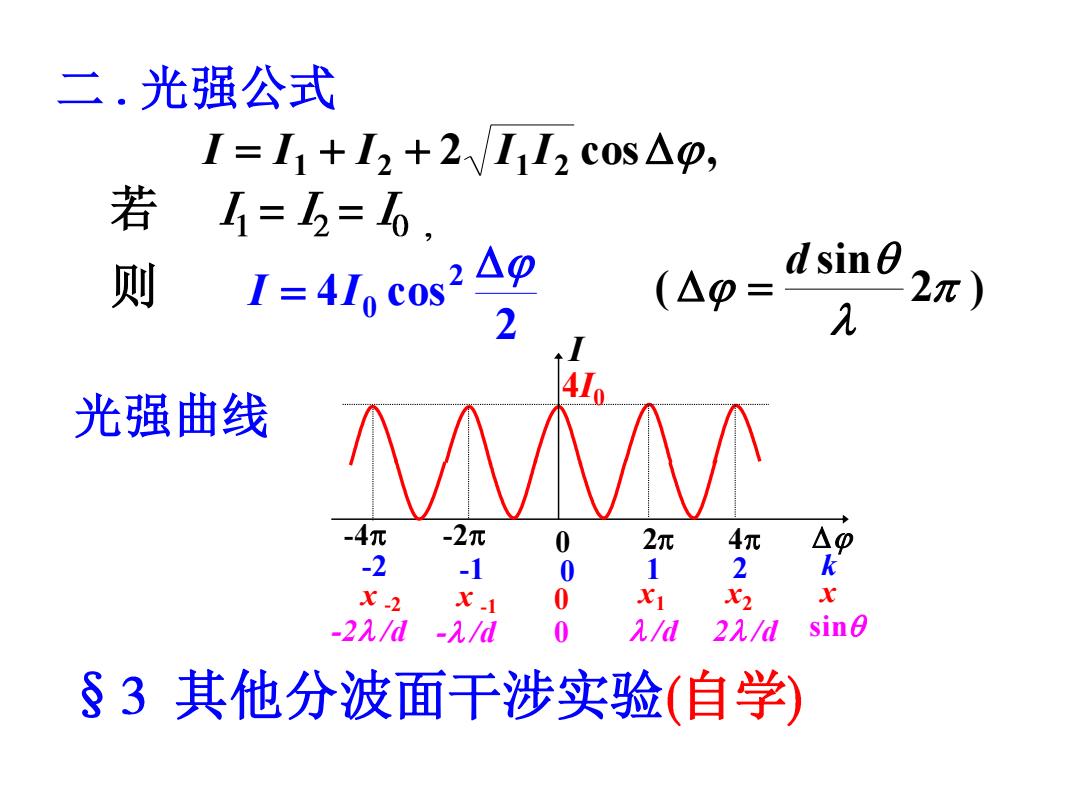
二.光强公式 I=I+12+2II2 CosAg, 若=五=6 则 1=410 cos2Ag (Ag=dsine r) 2 41 光强曲线 -4元 -2元 2元 0 X2 2/d2/dsin §3其他分波面干涉实验(自学)
二 光强公式 2 cos , I = I1 + I2 + I1 I2 若 2 4 cos2 0 则 I = I 2 ) sin ( d = 光强曲线 I -4 -2 0 2 4 -2 -1 0 1 2 k 4I0 x 0 x1 x2 x -2 x -1 -2 /d - /d 0 /d 2 /d sin § 其他分波面干涉实验 自学
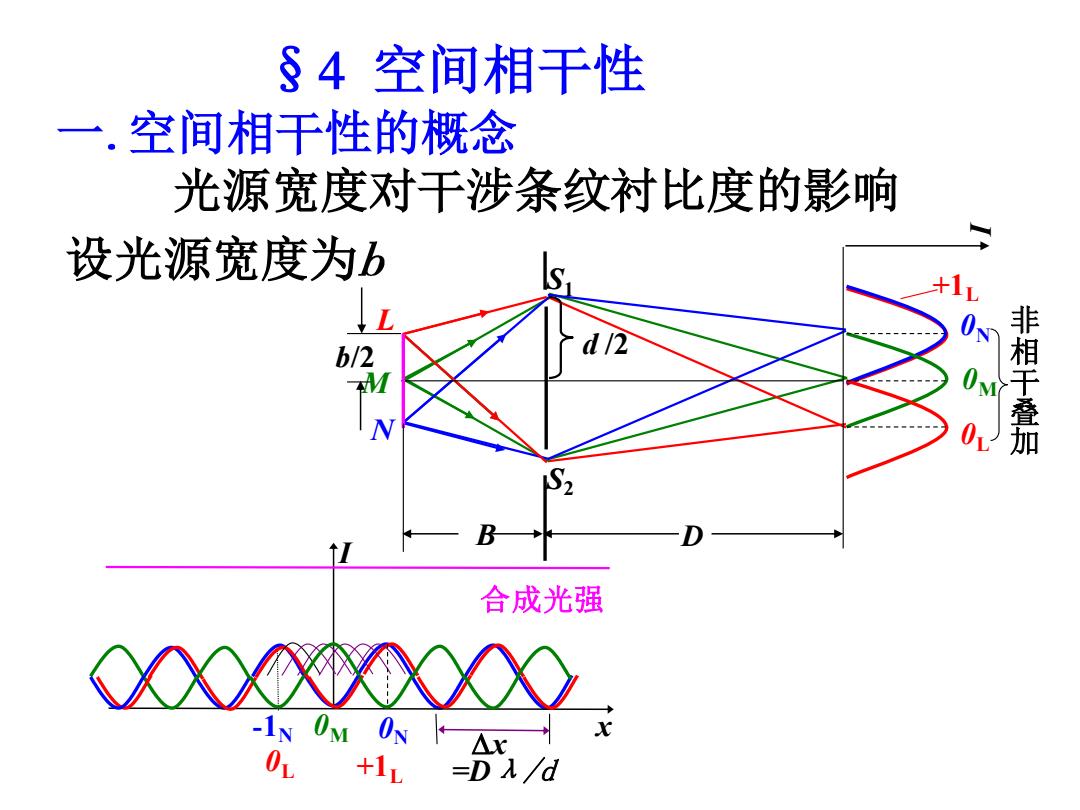
§4空间相干性 一.空间相干性的概念 光源宽度对干涉条纹衬比度的影响 设光源宽度为b h/2 《 0 相干叠加 B 合成光强 XXXX0XXXX 0+1L=Dλd
§ 空间相干性 一 空间相干性的概念 光源宽度对干涉条纹衬比度的影响 设光源宽度为 B D I 非 相 干 叠 加 +1L 0N 0M 0L b/2 d /2 L M N S1 S2 x I 合成光强 0N x +1L 0M 0L -1N =Dλ/d
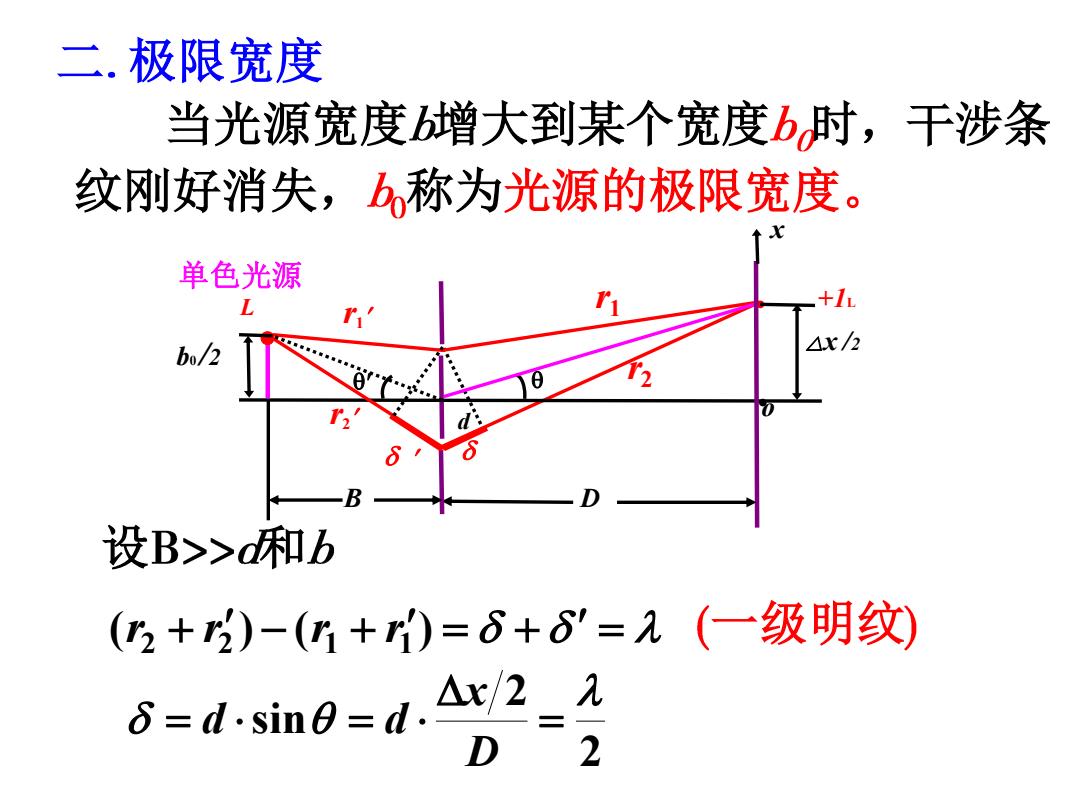
二.极限宽度 当光源宽度增大到某个宽度b时,干涉条 纹刚好消失,b称为光源的极限宽度。 单色光源 bo/2 设B>>d和b (2+)-(+)=6+8=入(一级明纹) 6=d.sine=d.Ax2A D 2
二 极限宽度 当光源宽度 增大到某个宽度 时,干涉条 设 和 (r2 + r2 ) − (r1 + r1 ) = + = 一级明纹 2 2 sin = = = D x d d 纹刚好消失, 称为光源的极限宽度。 d o B D · +1L r2 r1 • r1 r2 单色光源 b0 /2 · x L △x /2