
第三章电磁感应 electromagnetic induction 奥斯特 电流磁效应 对称性 磁的电效应? 反映了物质世界对称的 美 §1法拉第电磁感应定律 一.电磁感应现象
第三章 电磁感应 electromagnetic induction 奥斯特 电流磁效应 对称性 磁的电效应? 反映了物质世界对称的 §1 法拉第电磁感应定律 一.电磁感应现象 美
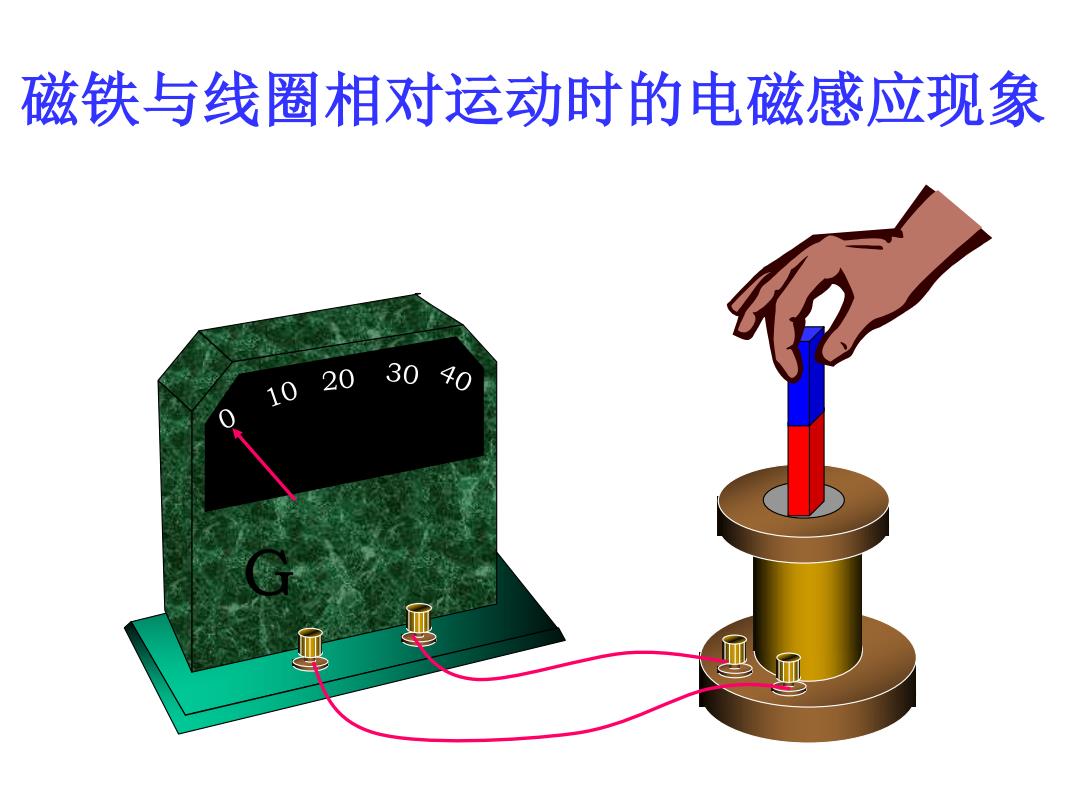
磁铁与线圈相对运动时的电磁感应现象 1020 3040
G 磁铁与线圈相对运动时的电磁感应现象
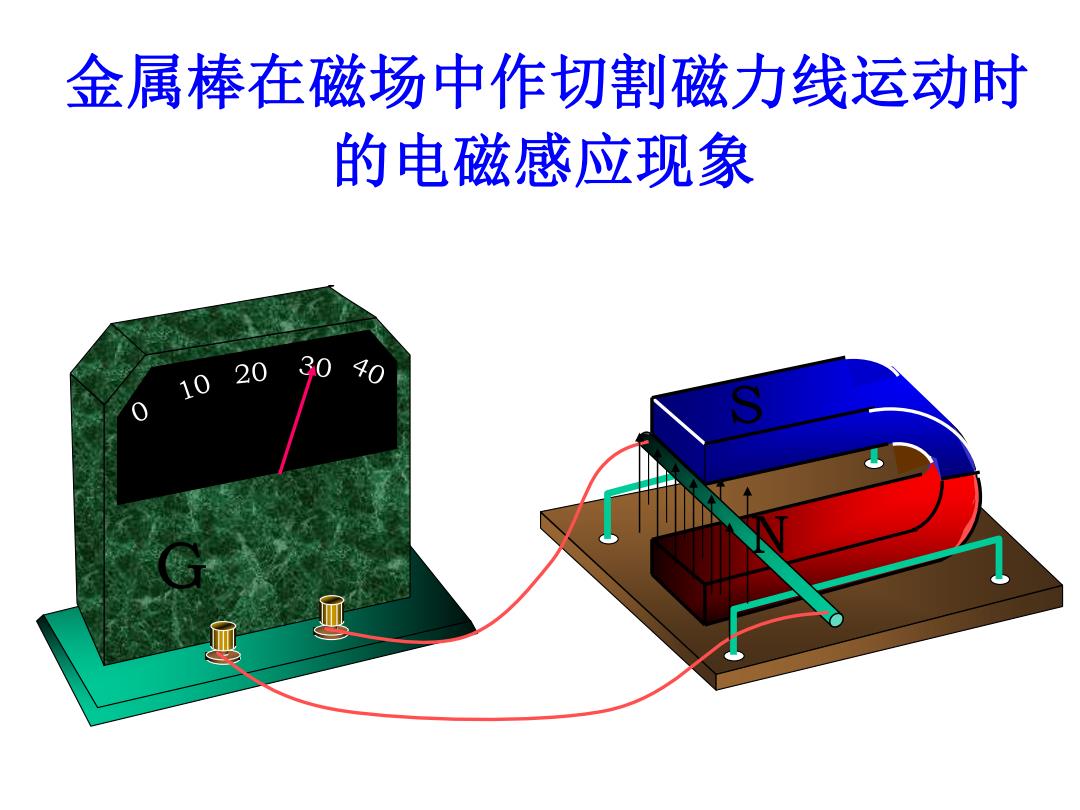
金属棒在磁场中作切割磁力线运动时 的电磁感应现象 1020 300
G S N 金属棒在磁场中作切割磁力线运动时 的电磁感应现象
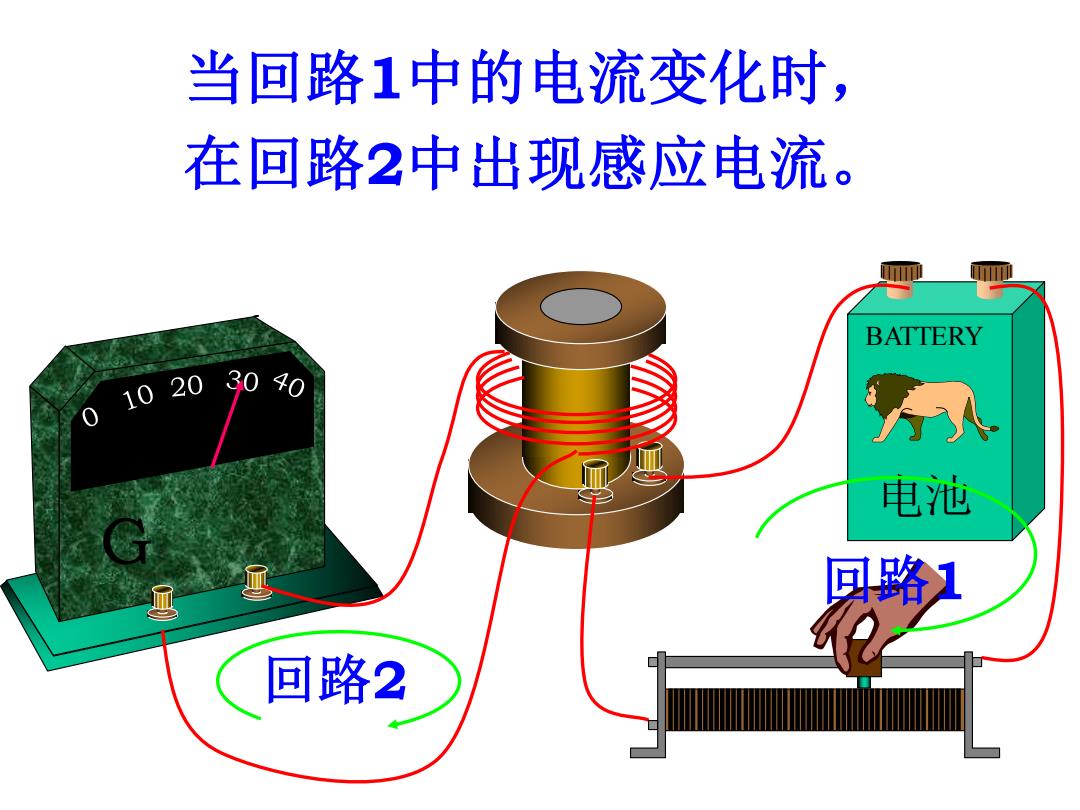
当回路1中的电流变化时, 在回路2中出现感应电流。 BATTERY 102000 0 电池 回路1 回路2
电池 BATTERY G 回路1 回路2 当回路1中的电流变化时, 在回路2中出现感应电流

二.规律 1.法拉第电磁感应定律 感应电动势的大小 d中 dt 2.楞次定律Lenz law 闭合回路中感应电流的方向,总是使它所激发 的磁场来阻止引起感应电流的磁通量的变化。 楞次定律是能量守恒定律在电磁感应现象上的 具体体现
二. 规律 1. 法拉第电磁感应定律 感应电动势的大小 i d dt = 2. 楞次定律 Lenz law 闭合回路中感应电流的方向,总是使它所激发 的磁场来阻止引起感应电流的磁通量的变化。 楞次定律是能量守恒定律在电磁感应现象上的 具体体现

3.法拉第电磁感应定律 dφ dt 约定 首先任定回路的绕行方向 规定电动势方向与绕行方向一致时为正 当磁力线方向与绕行方向成右手螺旋时 规定磁通量为正
3. 法拉第电磁感应定律 i d dt = − 约定 首先任定回路的绕行方向 规定电动势方向与绕行方向一致时为正 当磁力线方向与绕行方向成右手螺旋时 规定磁通量为正
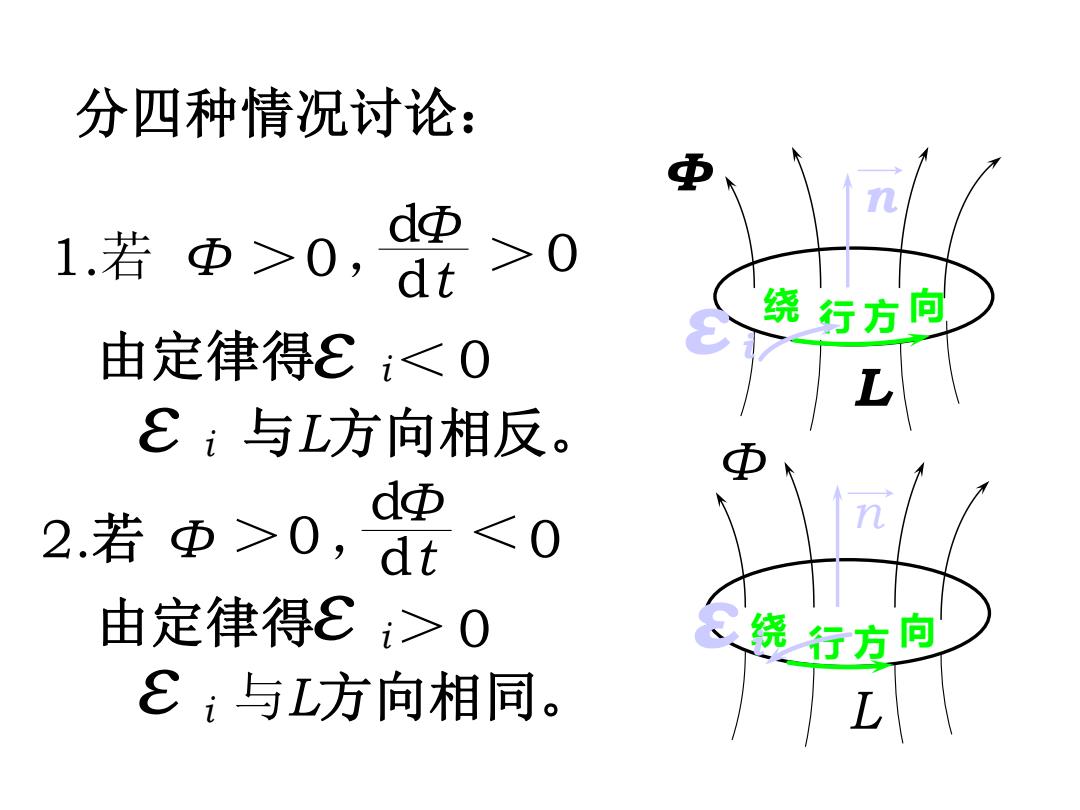
分四种情况讨论: dΦ 1.若Φ>0,dt >0 方 由定律得E0,d 0 之绕行方回 £:与L方向相同。 L
分四种情况讨论: d 1.若 Φ >0,dt >0 Φ 由定律得ε i<0 ε i 与L方向相反。 由定律得ε i> 0 ε i 与L方向相同。 d 2.若 Φ >0,dt <0 Φ Φ n L 绕 行 方 向 绕 行 方 向 n Φ L ε i ε i
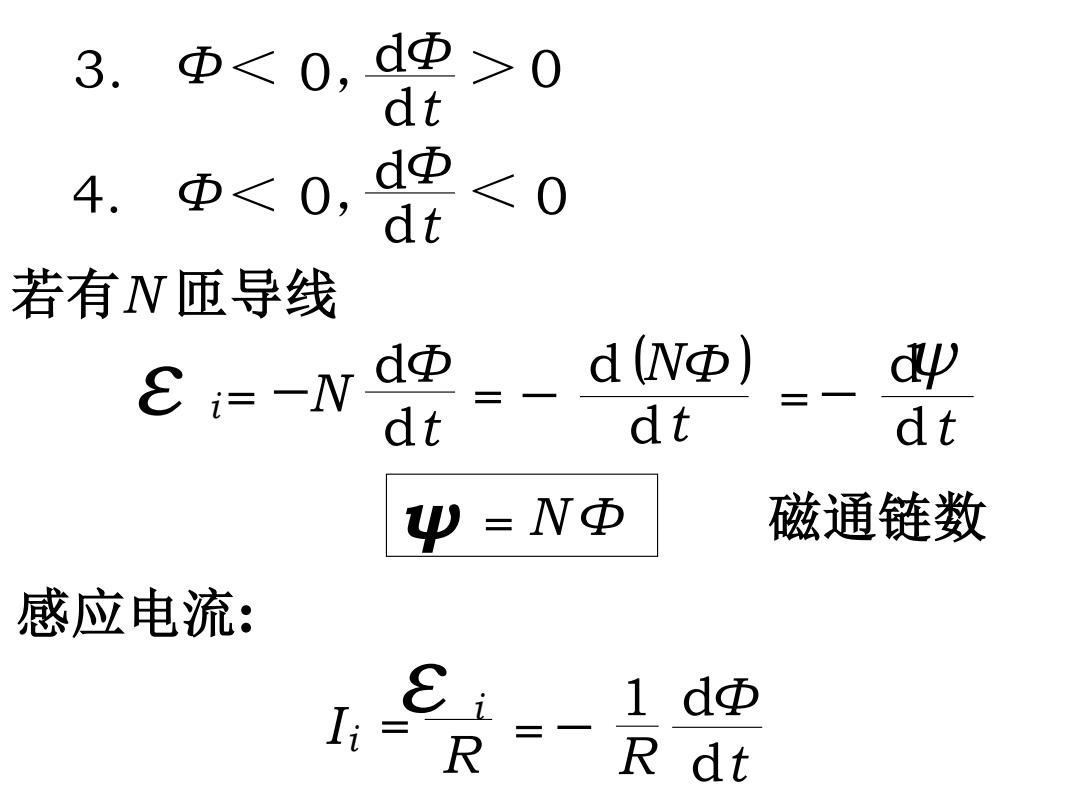
3. Φ0 t 4. Φ<0, dΦ dt ∠0 若有N匝导线 E=-wd地 dNΦ) dp dt dt dt ψ=NΦ 磁通链数 感应电流: 1dΦ R-R di
若有N 匝导线 ε i= d dt Φ N dψ = dt ψ = N Φ 磁通链数 感应电流: = R 1 d dt Φ d Φ = N dt ( ) d dt 3. Φ< 0, Φ > 0 d < dt Φ 4. Φ< 0, 0 ε I R i i =

例:直导线通交流电置于磁导率为μ的介质中 求:与其共面的匝矩形回路中的感应电动势 已知I=1 sin ot 其中In和o是大于零的常数 解:设当I>0时,电流方向如图 d-a 设回路L方向如图建坐标系如图 在任意坐标处取一面元忑 w=Nφ=NB.d5
例:直导线通交流电 置于磁导率为的介质中 求:与其共面的N匝矩形回路中的感应电动势 解:设当I 0时,电流方向如图 L I = = N N B dS S l d a I I sint 已知 = 0 其中 I0 和 是大于零的常数 设回路L方向如图 o x 建坐标系如图 在任意坐标处取一面元 ds ds

d+a y=Nb=NBs=NBs=N了 2πx Null,d+a 2π =HNl d+a ds 2π o sinotInd d-a dy 8=- dt =_Mol,NIola cos otln d+a 交变的 2π d 电动势
= = N N B dS S ldx x I N d a d + = 2 = N Il d + a d 2 ln = + NI l t d a d 0 2 sin ln d d a t N I l r + = − cos ln 2 0 0 = S N Bds dt d i = − 交变的 电动势L I l d a o x ds