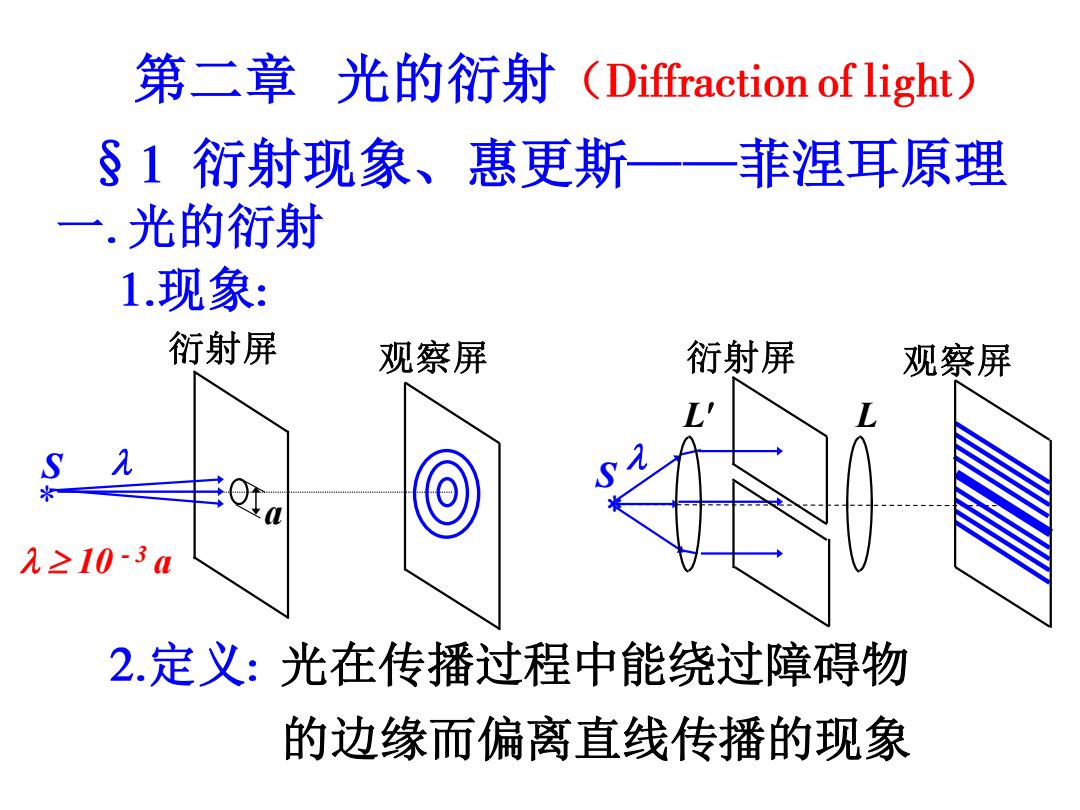
第二章 光的衍射(Diffraction of light) §1衍射现象、惠更斯——菲涅耳原理 一.光的衍射 1.现象: 衍射屏 观察屏 衍射屏 观察屏 L' L S 050 S ≥10-3a 2.定义:光在传播过程中能绕过障碍物 的边缘而偏离直线传播的现象
第二章 光的衍射( ) § 衍射现象、惠更斯 菲涅耳原理 一 光的衍射 现象 * S 衍射屏 观察屏 a 10 - 3 a 定义 光在传播过程中能绕过障碍物 * S 衍射屏 观察屏 L L 的边缘而偏离直线传播的现象
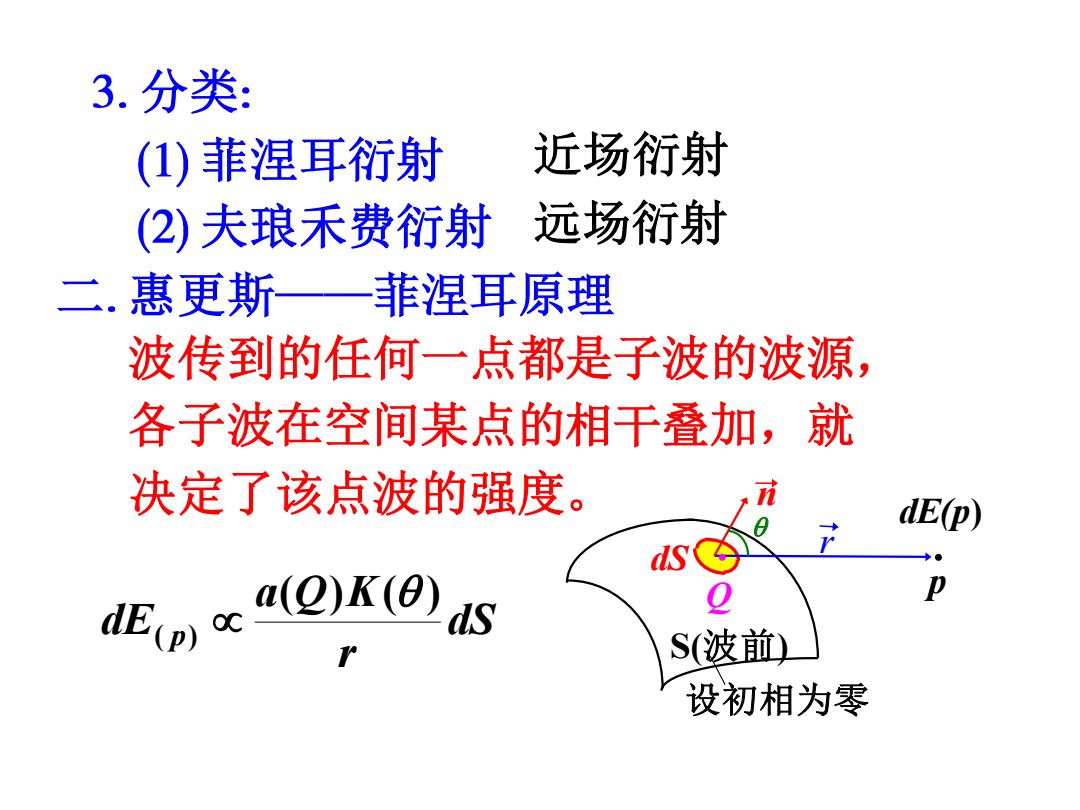
3.分类: (1)菲涅耳衍射 近场衍射 (②)夫琅禾费衍射远场衍射 二.惠更斯一菲涅耳原理 波传到的任何一点都是子波的波源, 各子波在空间某点的相干叠加,就 决定了该点波的强度。 9 dE(p) K()s 0 S(波前) 设初相为零
二 惠更斯 菲涅耳原理 波传到的任何一点都是子波的波源, · p · dE(p) r Q dS S(波前) 设初相为零 n 夫琅禾费衍射 远场衍射 菲涅耳衍射 近场衍射 分类 dS r a Q K dE p ( ) ( ) ( ) 各子波在空间某点的相干叠加,就 决定了该点波的强度

0=0,K=K max 《阳)方向因子 0个→K(0) π K=0 (Q)取决于波前上Q点处的强度 E()K(dS.cos Ep()).cs 2) =Ep)·c0s(0t+pp)) P处波的强度Ip Eip)
) 2 cos( ( ) ( ) ( ) r dS t r a Q K dE p − = dS r t r a Q K E p s − = ) 2 cos( ( ) ( ) ( ) cos( ) 0( p) p) = E t +( 处波的强度 2 p E0( p) I a(Q) 取决于波前上 点处的强度 = → = = , 0 2 ( ) 0, max K K K K 方向因子
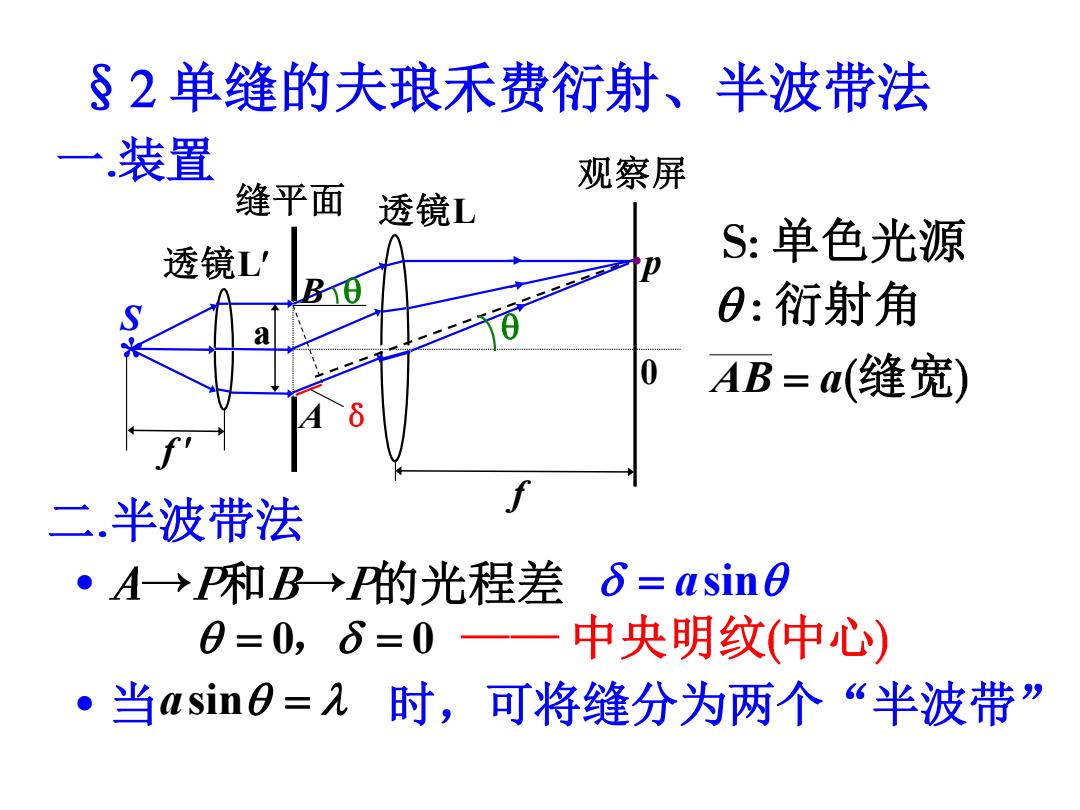
§2单缝的夫琅禾费衍射、半波带法 一装置 观察屏 缝平面 透镜L 透镜L S:单色光源 0:衍射角 AB=a(缝宽) 二.半波带法 ·A→和B→P的光程差6=asin O 0=0,6=0—一中央明纹(中心) ·当asin0=2时,可将缝分为两个“半波带
§ 单缝的夫琅禾费衍射、半波带法 一 装置 * S f f a 透镜L 透镜L ·p A B 缝平面 观察屏 0 δ 二 半波带法 AB = a 缝宽 单色光源 衍射角 = asin = 0, = 0 中央明纹 中心 当 asin = 时,可将缝分为两个“半波带” 和 的光程差
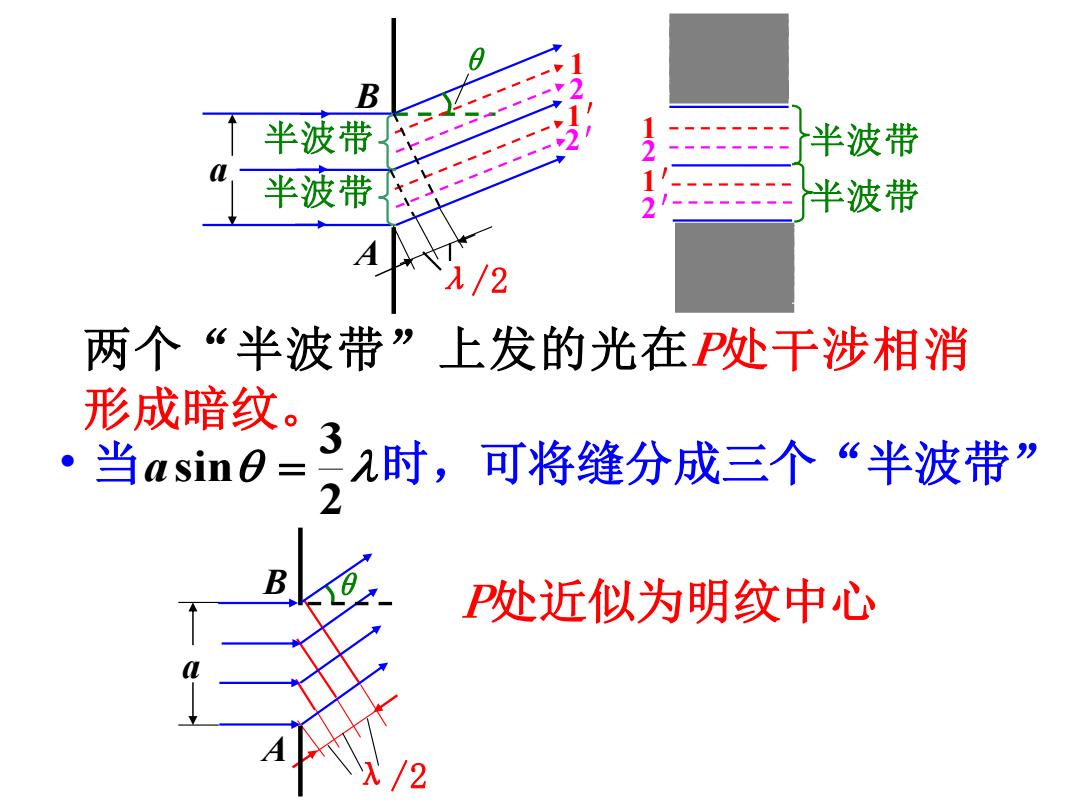
B 半波带 二半波带 半波带 半波带 λ/2 两个“半波带”上发的光在P处干涉相消 形成暗纹。3 ·当asin0=λ时,可将缝分成三个“半波带” P处近似为明纹中心 2
a θ 1′ B 2 A 半波带 半波带 1 2′ 两个“半波带”上发的光在 处干涉相消 形成暗纹。 • 当 时,可将缝分成三个“半波带” 2 3 a sin = 处近似为明纹中心 a λ/2 B θ A λ/2 半波带 半波带 1 2 1′ 2′

·当asin0=2元 时,可将缝分成四个“半波 带”形成暗纹。 一般情况 asin0=±k2,k=1,2,3 暗纹 asin0=±(2k+1)2, k'=1,2,3… 明纹(中心) asin0 =0 中央明纹(中心) 上述暗纹和中央明纹(中心)位置是准确的, 其余明纹中心的位置较上稍有偏离
a λ/2 B A θ 形成暗纹。 • 当 时 可将缝分成四个“半波 带” a sin = 2 a sin = k,k = 1,2,3… 暗纹 , 1,2,3… 2 a sin = (2k + 1) k = 明纹 中心 a sin = 0 中央明纹 中心 上述暗纹和中央明纹 中心 位置是准确的, 其余明纹中心的位置较上稍有偏离。 一般情况
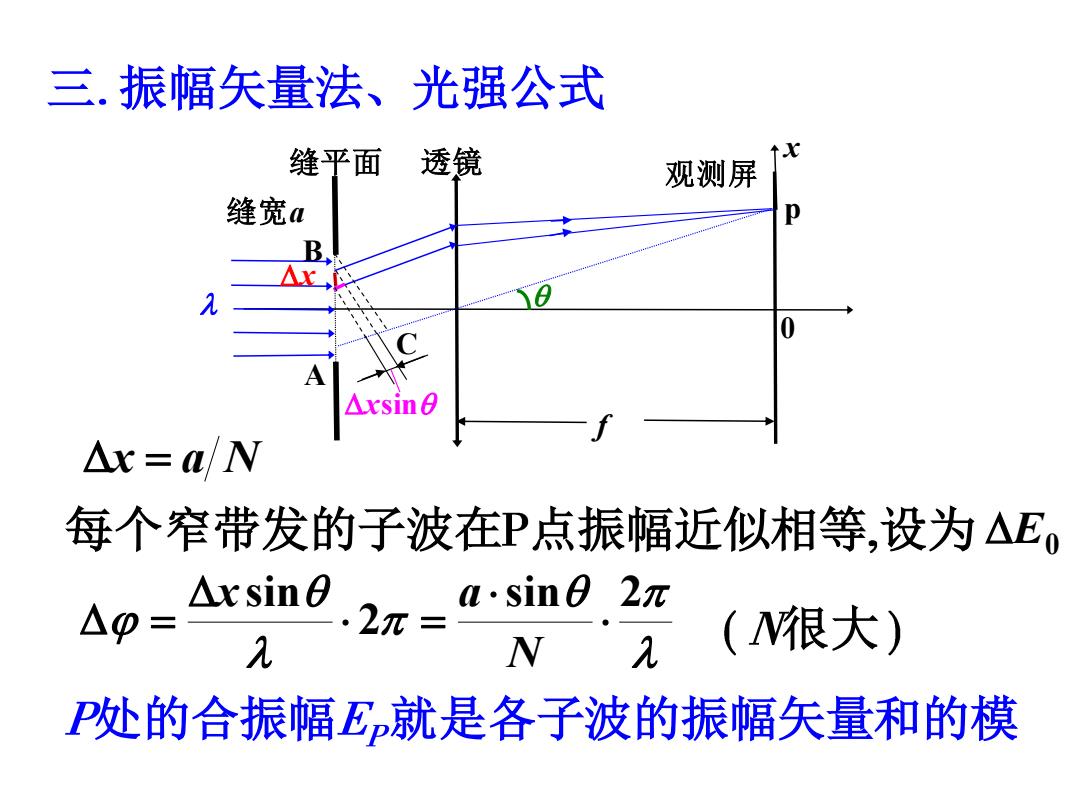
三.振幅矢量法、光强公式 缝平面透镜 ↑x 观测屏 缝宽a B △xsin △r=a/N 每个窄带发的子波在P点振幅近似相等,设为△E, △p= Axsine .2元=asin0.2r 元 N (很大) P处的合振幅E就是各子波的振幅矢量和的模
三 振幅矢量法、光强公式 x = a N sin 2 2 sin = = N x a 很大 每个窄带发的子波在 点振幅近似相等 设为 E0 处的合振幅 就是各子波的振幅矢量和的模 透镜 f p x x xsin 缝平面 缝宽a A B C 0 观测屏

P处是多个同方向、同频率、同振幅、初 相依次差一个恒量△φ的简谐振动的合成, 合成的结果仍为简谐振动。 对于O点: 0=0,△p=0 △E E=N△E Ep 对于其他点PEp<Eo E 4E,4p 当N→o∞时,个相接的折线将变为一个圆弧
处是多个同方向、同频率、同振幅、初 对于 点 E0 E0 …… 对于其他点 : EP E0 当 → 时 个相接的折线将变为一个圆弧。 相依次差一个恒量△ 的简谐振动的合成, 合成的结果仍为简谐振动

AΦ=Wap=asin8) 2π △Φ ,△Φ E=2Rsin , EO=R△④ R E-2sin .△Φ △Φ1 2-△Φ/2 2 令 △ΦπsinO Q= 2 有 En=Eo sina 又 IccE2 o P点的光强 I=0 sina
2 a sin = N = , 2 2 sin Ep = R E0 = R2 sin 2 2 2 sin 0 0 = = E E E p 令 sin 2 a = = 有 sin E p = E 0 又 2 0 0 2 I E p ,I E 点的光强 2 0 sin = I I R EP E 0 △ Φ △ Φ

由1=10 sina 可得 (1)主极大(中央明纹中心)位置: 0=0处,a=0→ina-1→1=l,=1an (2)极小(暗纹)位置: a=±km,k=1,2,3.时,sina=0→I=0 由a=πasin0=士kz得asin0=士k2 λ 或 N△p=±2kπ→asin0=±k兄 (3)次极大位置: d =0→tga=a da
由 可得 2 0 sin = I I 主极大(中央明纹中心)位置: 1 0 max sin = 0 = 0 → = → I = I = I 处 , 极小(暗纹)位置: = k,k = 1,2,3时,sin = 0 → I = 0 由 得 sin k a = = asin = k 或 N = 2k → asin = k = 0 → tg = d dI 次极大位置: