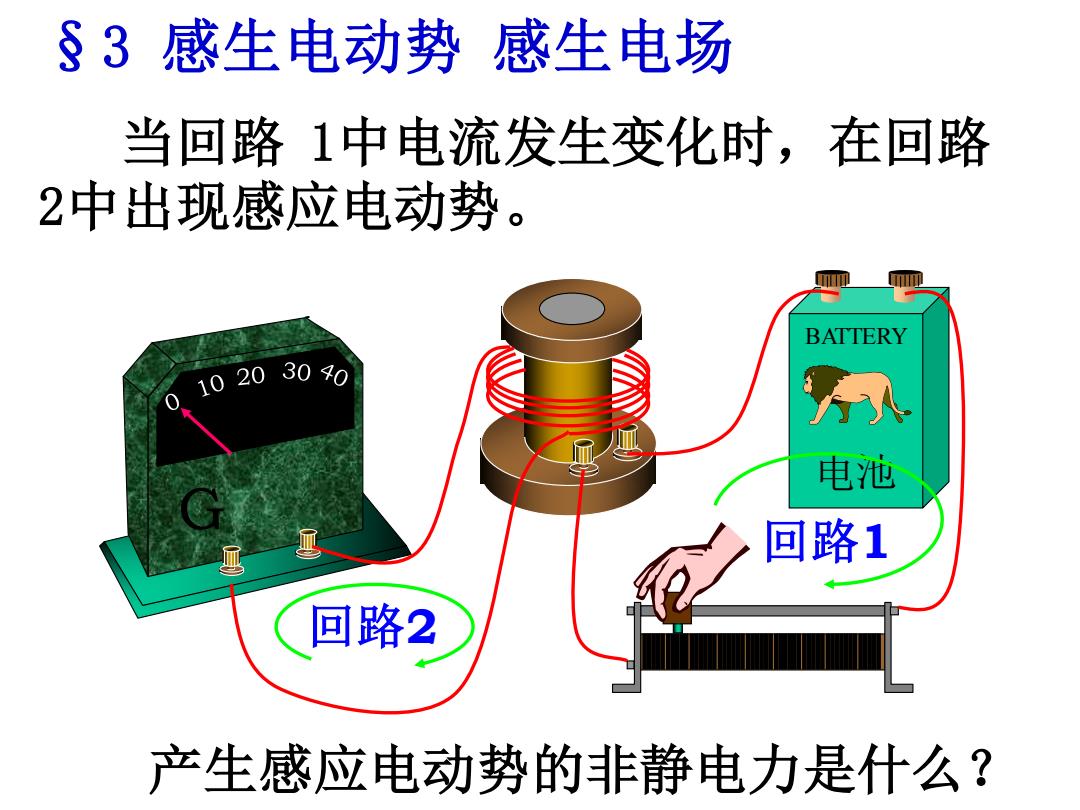
§3感生电动势感生电场 当回路1中电流发生变化时,在回路 2中出现感应电动势。 BATTERY 1020300 电池 回路1 回路2 产生感应电动势的非静电力是什么?
当回路 1中电流发生变化时,在回路 2中出现感应电动势。 产生感应电动势的非静电力是什么? 回路2 电池 BATTERY G 回路1 §3 感生电动势 感生电场
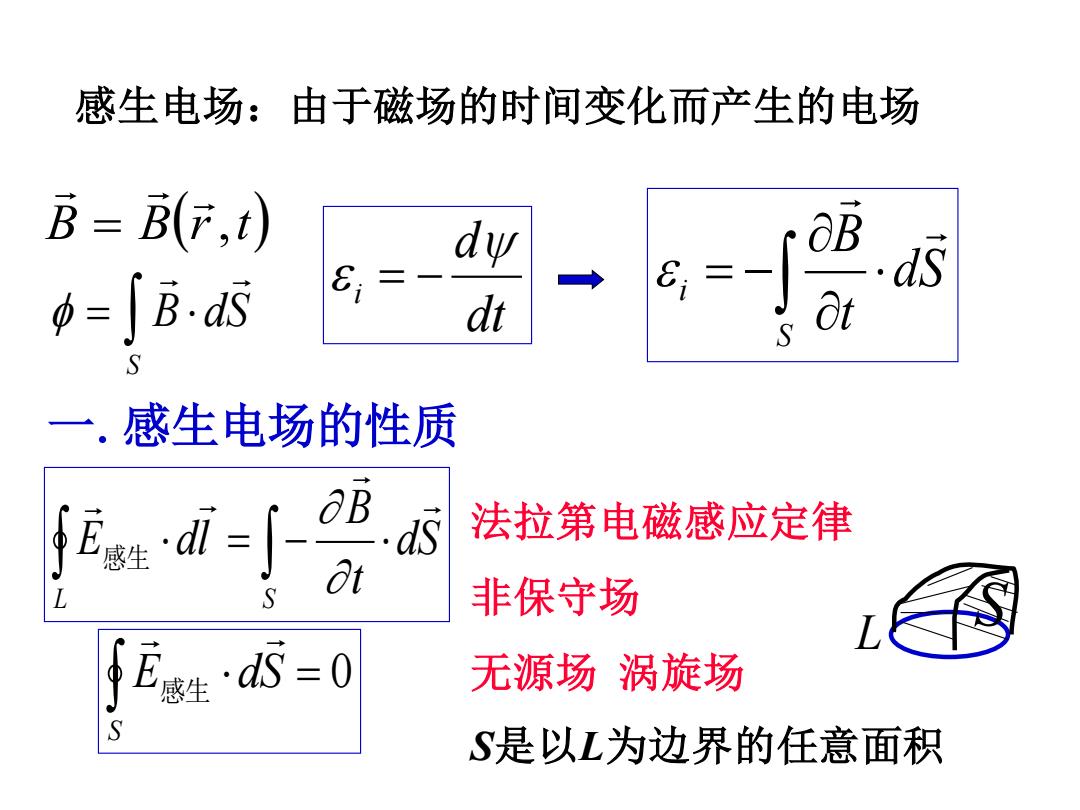
感生电场:由于磁场的时间变化而产生的电场 B=(厅,t) ds p=∫BS dt 一.感生电场的性质 6B 法拉第电磁感应定律 非保守场 E生=0 无源场涡旋场 S是以L为边界的任意面积
( ) B = B r,t = B dS S 一.感生电场的性质 dS t B E dl L S = − 感生 = 0 S E dS 感生 法拉第电磁感应定律 非保守场 无源场 涡旋场 S是以L为边界的任意面积L S dt d i = − = − S i dS t B 感生电场:由于磁场的时间变化而产生的电场
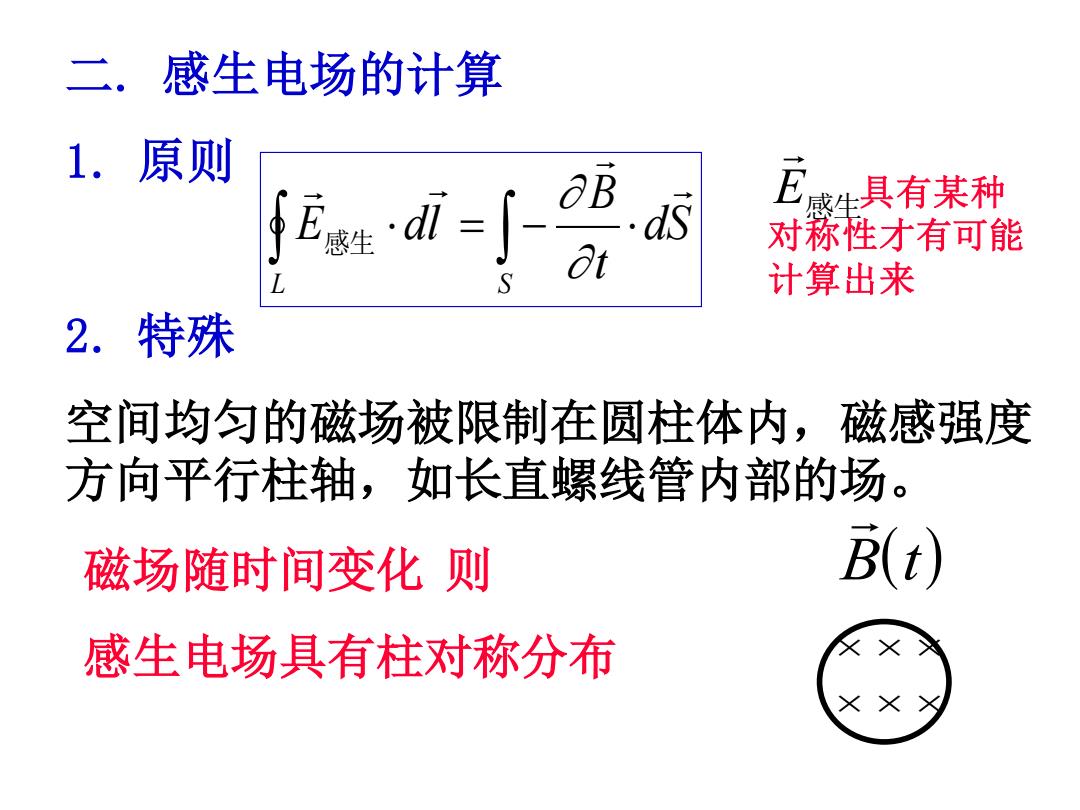
二. 感生电场的计算 1.原则 Ew姓d-∫ dS a 尼感生具有某种 对称性才有可能 计算出来 2.特殊 空间均匀的磁场被限制在圆柱体内,磁感强度 方向平行柱轴,如长直螺线管内部的场。 磁场随时间变化则 (t) 感生电场具有柱对称分布 ××
二. 感生电场的计算 1. 原则 dS t B E dl L S = − 感生 2. 特殊 空间均匀的磁场被限制在圆柱体内,磁感强度 方向平行柱轴,如长直螺线管内部的场。 磁场随时间变化 则 感生电场具有柱对称分布 ( ) B t 具有某种 对称性才有可能 计算出来 E感生
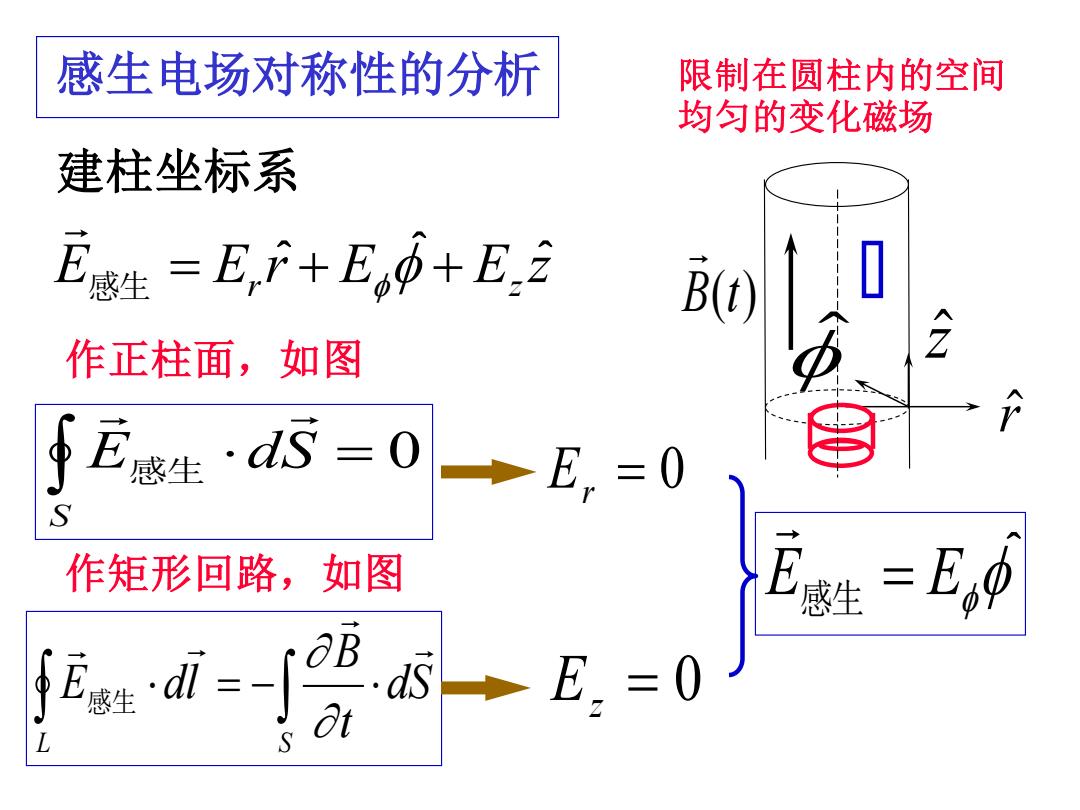
感生电场对称性的分析 限制在圆柱内的空间 均匀的变化磁场 建柱坐标系 Es生=E,F+E,0+E,2 B() 作正柱面,如图 ∮E感生·dS =0 E.=0 作矩形回路,如图 =E0 f Eaa'dl=- E.=0
r z 作正柱面,如图 = 0 E dS S 感生 Er = 0 dS t B E dl L S = − 感生 Ez = 0 感生电场对称性的分析 B(t) 限制在圆柱内的空间 均匀的变化磁场 建柱坐标系 E E r E E z 感生 = r + + z ^ ^ ^ 作矩形回路,如图 E感生 = E ^

3.特殊情况下感生电场的计算 空间均匀的磁场限制在半径为R 的圆柱内,B的方向平行柱轴 且有 dB dt 求:E感生分布 解:设场点距轴心为r,根据对称性,取以 o为心,过场点的圆周环路L dB ∫E姓·d=Ew姓2πr 由法拉第电 磁感应定律 =-S dt
3. 特殊情况下感生电场的计算 空间均匀的磁场限制在半径为 R 的圆柱内, 求: 感生 E 分布 解:设场点距轴心为r ,根据对称性,取以 o为心,过场点的圆周环路 L E dl E r L 感生 = 感生 2 B • 0 L r dt dB = −S 由法拉第电 磁感应定律 B 的方向平行柱轴 c dt dB 且有 =

XR S=πr r dB S dB E感生= E感生 2 dt 2πrdt r>RS=πR2 R2dB 2r dt dB >0 E,0
0 i 0 dt dB > dt dB r S E 2 = − 感生 2 r R S =R dt dB r R E 2 2 = − 感生

讨论 r dB E感生 特殊条件 2 dt 电子感应加速器的 R2 dB E感生 基本原理1947年 2r dt 世界第一台7OMeV 感生电场是以法拉第电磁感应定律为基础的, 源于法拉第电磁感应定律又高于法拉第电磁感应 定律。只要以L为边界的曲面内有磁通的变化,就 存在感生电场的。 涡电流趋肤效应
dt dB r R E dt r dB E 2 2 2 = − = − 感生 感生 特殊条件 感生电场是以法拉第电磁感应定律为基础的, 源于法拉第电磁感应定律又高于法拉第电磁感应 定律。只要以L为边界的曲面内有磁通的变化,就 存在感生电场的。 涡电流 趋肤效应 电子感应加速器的 基本原理 1947年 世界第一台 70MeV 讨论

求半径o线上的感生电动势 B(N ER 感生= 「龙d=0 b R) 可利用这一特点较方便地求其他线段内的感生电动势 补上半径方向的线段构成回路利用法拉第电磁感应定律 例求上图中线段ab内的感生电动势 解:补上两个半径oa和bo与b构成回路obao dg 6;=8ob+8ba+8ao= dt dB 6o=06o6=0 Eba=-S dt
求半径oa线上的感生电动势 ( ) = = R E dl 0 E ⊥R 感生 感生 可利用这一特点较方便地求其他线段内的感生电动势 补上半径方向的线段构成回路利用法拉第电磁感应定律 例 求上图中 线段ab内的感生电动势 解:补上两个半径oa和bo与ab构成回路obao dt d i o b b a a o = + + = − = 0 = 0 ao ob dt dB S ba = − B(t) • b o a

又如磁力线限制在圆 dB B 柱体内,空间均匀 Q 求:Bab 解:补上半径0ab0 设回路方向如图 do Eoabo Eoa +Eab +bo =0 dt E6=0 dφ dB dt 中=BS扇形 Eab =一S扇形 dt
求 : ab 解:补上半径 oa bo 设回路方向如图 oabo oa ab bo d dt = + + = − oa = 0 bo = 0 ab d dt = − = BS扇形 dt dB a b = − S 扇形 又如磁力线限制在圆 柱体内, 空间均匀 dB dt = c o B a b

4.感生电场与静电场比较: a.静电场是有势无旋场,感生电场是有 旋无势场; b.静电场的电场线是“有头有尾”的, 生电场的电场线是一组闭合曲线。 c.静电场是由静止电荷产生的,感生电 场是由变化磁场产生的
b. 静电场的电场线是“有头有尾”的,感 生电场的电场线是一组闭合曲线。 4. 感生电场与静电场比较: c. 静电场是由静止电荷产生的,感生电 场是由变化磁场产生的。 a. 静电场是有势无旋场,感生电场是有 旋无势场;