西安电子科技大学：《大学物理》课程习题解答（力学）第9章振动习题解答.doc_大学文库

第9章振动习题解答 60 第9章振动习题解答第九章基本知识小结 ⒈物体在线性回复力 F = - kx，或线性回复力矩τ= - cφ作用下的运动就是简谐振动，其动力学方程为 0, 2 2 0 2 + x = dt d x  （x 表示线位移或角位移）；弹簧振子：ω0 2=k/m，单摆：ω0 2=g/l，扭摆： ω0 2=C/I. ⒉简谐振动的运动学方程为 x = Acos(ω0t+α)；圆频率、频率、周期是由振动系统本身决定的，ω0=2π/T=2πv；振幅 A 和初相α 由初始条件决定。 ⒊在简谐振动中，动能和势能互相转换，总机械能保持不变；对于弹簧振子， 2 2 2 0 2 1 2 1 Ek + Ep = kA = m A 。 ⒋两个简谐振动的合成分振动特点合振动特点方向相同，频率相同与分振动频率相同的简谐振动 Δα=±2nπ 合振幅最大 Δα=±(2n+1)π 合振幅最小方向相同，频率不同，频率成整数比不是简谐振动，振动周期等于分振动周期的最小公倍数方向相同，频率不同，频率较高，又非常接近出现拍现象，拍频等于分振动频率之差方向垂直，频率相同运动轨迹一般为椭圆 Δα=±2nπ 简谐振动（ⅠⅢ象限） Δα=±(2n+1)π简谐振动(ⅡⅣ象限) 方向垂直，频率不同，频率成整数比利萨如图形，花样与振幅、频率、初相有关 ⒌阻尼振动的动力学方程为 2 0 2 2 0 2 + + x = dt dx dt d x   。其运动学方程分三种情况： ⑴在弱阻尼状态（β＜ω0），振动的方向变化有周期性， 2 2 0 cos(' ), '    = + = − − x Ae t t ，对数减缩 = βT’. ⑵在过阻尼状态（β＞ω0），无周期性，振子单调、缓慢地回到平衡位置。 ⑶临界阻尼状态（β=ω0），无周期性，振子单调、迅速地回到平衡位置 ⒍受迫振动动力学方程 x f t dt dx dt d x 2  0 cos 2 2 0 2 + + = ；其稳定解为 cos( ) x = A0 t + ，ω是驱动力的频率，A0 和φ也不是由初始条件决定, 2 2 2 2 2 A0 = f 0 / (0 − ) + 4  2 2 0 2     − tg = − 当 2 2  = 0 − 2 时，发生位移共振

第9章振动习题解答 61 第9章振动习题解答 9.2.1一刚体可绕水平轴摆动。已知刚体质量为m,其重心C和设m向下偏离平衡位置x,弹簧1伸长△L1,弹簧2 轴O间的距离为h,刚体对转动轴线的转动惯量为I。问刚体围绕平伸长△L2,△L1+△L2=x(1):由于忽略弹簧质量，衡位置的微小摆动是否是简谐振动？如果是，求固有频率，不计一两个弹簧连接点处所受的两个弹力等大反向，即切阻力。 m k△L1=k△L2(2:、(2②解得：AL2=x, 07 解：规定转轴正方向垂直纸面向外，忽略一切阻力，则刚体所受力矩t=,mghsin中因为是微小摆动，sin中≈中，∴.T=.mgh中，所以m所受的回复力F=-k△L,=一能x, 即刚体是在一线性回复力矩作用下在平衡位置附近运动，因而是简谐振动。由牛顿二定律：-能x=m产，即杂+x=0 由转动定理：-mghφ=1d2p/dh2 0,'=√始，未串联前频率0，=臣，令0，=0，即即，#+警中=0∴0,2=竿，0。=学 √=V停，可求得：k=k kk: 9.2.2轻弹簧与物体的连接如图所示，物体质量为m,弹簧的劲 9.2.4单摆周期的研究：(1)单摆悬挂于以加速度α沿水平方向直度系数为k1和k2,支承面为理想光滑面，求系统振动的固有频率。线行驶的车厢内：(2)单摆悬挂于以加速度α上升的电梯内：(3)单摆解：以平衡位置为原点建立 k k2 悬挂于以加速度a(a<g)下降的电梯内。求此三种情况下单摆的周坐标0-x。设m向右偏离平衡位 MiM 期，摆长为1 置x,则弹簧1被拉长x,弹簧2 0 解：()以车为参考系，单摆受力如图示，被压缩x,m所受的合力（即回复力）F=-(k1+k2)x 设平衡位置与竖直线成α角，由平衡条件： Tsin a=ma,T cosa mg,..tga=a/g 由牛顿第二定律：-（化，+人2）x=m容，亲+泸x=0 设单摆偏离平衡位置角位移为0(9<5°)，单摆所受回复力矩： =-[mglsin a+0)-malcos(a+0)] =-mlg(sin a cos0+cosasin 0)-a(cosa cos0-sin asin 0)] 9.2.3一垂直悬挂的弹簧振子，振子质量为m,弹簧的劲度系数 0<5°，cos0≈1，sn0≈0，gsin a=acosa 为k1.若在振子和弹簧k1之间串联另一弹簧，使系统的频率减少一半。 T-mlg(smn a+0 cosa)-a(cosa-0sin a)] 问串联上的弹簧的劲度系数k虹应是k:的多少倍？ =-ml(g cosa+asin a)0 解：以两个弹簧串联后m的平衡位置为原点建立图示坐标o-x, 由转动定理：邛=t,m2碧=-ml(gcosa+asna)

第9章振动习题解答 61 第9章振动习题解答 9.2.1 一刚体可绕水平轴摆动。已知刚体质量为 m，其重心 C 和轴 O 间的距离为 h，刚体对转动轴线的转动惯量为 I。问刚体围绕平衡位置的微小摆动是否是简谐振动？如果是，求固有频率，不计一切阻力。解：规定转轴正方向垂直纸面向外，忽略一切阻力，则刚体所受力矩τ= - mghsinφ O h 因为是微小摆动，sinφ≈φ,∴τ= - mghφ，即刚体是在一线性回复力矩作用下在平衡位 φ C 置附近运动，因而是简谐振动。由转动定理： 2 2 − mgh = Id  / dt mg 即， I mgh I mgh I mgh dt d + =  = 0 = 2 0 0 , 2 2     9.2.2 轻弹簧与物体的连接如图所示，物体质量为 m，弹簧的劲度系数为 k1 和 k2，支承面为理想光滑面，求系统振动的固有频率。解：以平衡位置为原点建立 k1 k2 坐标 o-x。设 m 向右偏离平衡位置 x，则弹簧 1 被拉长 x，弹簧 2 o x 被压缩 x，m 所受的合力（即回复力） F (k k )x = − 1 + 2 . 由牛顿第二定律： ( ) , 0 1 2 2 2 2 2 − 1 + 2 = + = + k k x m x m k k dt d x dt d x m k k m k k 1 2 1 2 0 2 0 , + +  =  = 9.2.3 一垂直悬挂的弹簧振子，振子质量为 m，弹簧的劲度系数为k1.若在振子和弹簧k1 之间串联另一弹簧，使系统的频率减少一半。问串联上的弹簧的劲度系数 k2 应是 k1 的多少倍？解：以两个弹簧串联后 m 的平衡位置为原点建立图示坐标 o-x, 设 m 向下偏离平衡位置 x，弹簧 1 伸长ΔL1，弹簧 2 k1 伸长ΔL2，ΔL1+ΔL2 = x (1)；由于忽略弹簧质量， k2 两个弹簧连接点处所受的两个弹力等大反向，即 k1ΔL1 = k2ΔL2 (2)；由⑴、⑵解得： L x k k k 1 2 1 2 +  = ， o 所以 m 所受的回复力 F k L x k k k k 1 2 1 2 2 2 + = −  = − ， x 由牛顿二定律； 2 2 1 2 1 2 dt d x k k k k − + x = m ，即 0 ( ) 1 2 1 2 2 2 + = + x m k k k k dt d x 0 ( ) 1 2 1 2 ' m k k k k +  = ，未串联前频率 m k1 0 = ，令 2 0 1 0  ' =  ，即 m k m k k k k 1 1 2 1 2 2 1 ( ) = + ，可求得： 3 1 1 2 k = k 9.2.4 单摆周期的研究：⑴单摆悬挂于以加速度 a 沿水平方向直线行驶的车厢内；⑵单摆悬挂于以加速度 a 上升的电梯内；⑶单摆悬挂于以加速度 a（a<g）下降的电梯内。求此三种情况下单摆的周期，摆长为 l. 解：⑴以车为参考系，单摆受力如图示，设平衡位置与竖直线成α角，由平衡条件： T sin  = ma,T cos = mg,tg = a / g 设单摆偏离平衡位置角位移为θ(θ<5°)，单摆所受回复力矩：                              ( cos sin ) [ (sin cos ) (cos sin )] 5 , cos 1, sin , sin cos [ (sin cos cos sin ) (cos cos sin sin )] [ sin( ) cos( )] ml g a ml g a g a ml g a mgl mal = − +  − + − −     = = − + − − = − + − + 由转动定理： , 2 ( cos sin ) 2 2      I ml ml g a dt d = = − + ， m m f*=ma T mg a α

第9章振动习题解答 62 第9章振动习题解答 2 2 2 2 2 2 2 2 , , 2 0, cos / ,sin / , 0 2 cos sin 0 cos sin 2 2 2 2 a g l l a g l a g l g a l g a dt d T g a g a a g + + + + +  = = = = + = = + = +            以上求解较为麻烦，我们可以用另外一种简捷的思路和方法：在重力场中单摆的周期为 g l T = 2 ，g 是重力场强度现在单摆在力场 mg mg f mg ma      ' = + * = − 中振动，力场强度： 2 2 ' , ' , 2 2 ' 2 2 g a l g l g g a g g a T + = − = +  =  =     ⑵以电梯为参考系，平衡位置仍然在铅直方向，由转动定理： 2 2 2 ( ) sin ( ) dt ml d mg ma l m g a l  − +   − +  = g a l l g a l g a dt d T + + + +  =  = =   2 0, 0 , 2 2 同样可以认为单摆在力场 mg mg ma    ' = − 中振动，力场强度： g a l g l g g a T + ' = + ,  = 2 = 2 ' ⑶与前面分析完全相同， g a l T − = 2 9.2.5 在通常温度下，固体内原子振动的频率数量级为 1013/s，设想各原子间彼此以弹簧连接，1 摩尔银的质量为 108g，且包含 6.02 ×1023 个原子，现仅考虑一列原子，且假设只有一个原子以上述频率振动，其它原子皆处于静止，计算一根弹簧的劲度系数。解：利用 9.2.2 题的结果： m k m k k 2 0 1 2 = = +  k m (2 10 ) 354N / m 13 2 6.02 10 108 10 2 1 2 2 0 1 2 3 3 = =    =   −   9.2.6 一弹簧振子，弹簧的劲度系数为 k=9.8N/m,物体的质量为 200g,现将弹簧自平衡位置拉长 2 2 cm 并给物体一远离平衡位置的速度，其大小为 7.0cm/s,求该振子的运动学方程（SI）。解：弹簧振子的圆频率 7 0.2 9.8 0 = = = m  k .设振子的运动学方程为 x = Acos(7t +) (1), v = = −7Asin( 7t +) (2) dt dx . 据题意,t=0 时， x 2 2 10 m,v 7.0 10 m /s −2 −2 =  =  ,代入⑴、 ⑵中，有 2 2 10 cos (1)',7.0 10 7 sin (2)' 2 2  = A   = − A  − − 由⑴'、⑵'可解得：A=3×10-2m； cos = 2 2 / 3,sin  = −1/ 3 , α= - 19.47º= - 0.34rad. 代入（1）中，振子的运动学方程为： x = 3×10-2 cos (7t - 0.34). 9.2.7质量为1.0×103g的物体悬挂在劲度系数为1.0×106dyn/cm 的弹簧下面，⑴求其振动的周期；⑵在 t=0 时，物体距平衡位置的位移为+0.5cm，速度为+15cm/s，求运动学方程。解：以平衡位置为坐标原点，建立图示坐标 o-x ⑴ 10 10 10 3 10 1.0 10 10 0 2 6 5 = = − = = −   m  k T 0.199s 10 10 2 2 0 = = =    k k ⑵设运动学方称为 x = Acos(10 10t +) O x

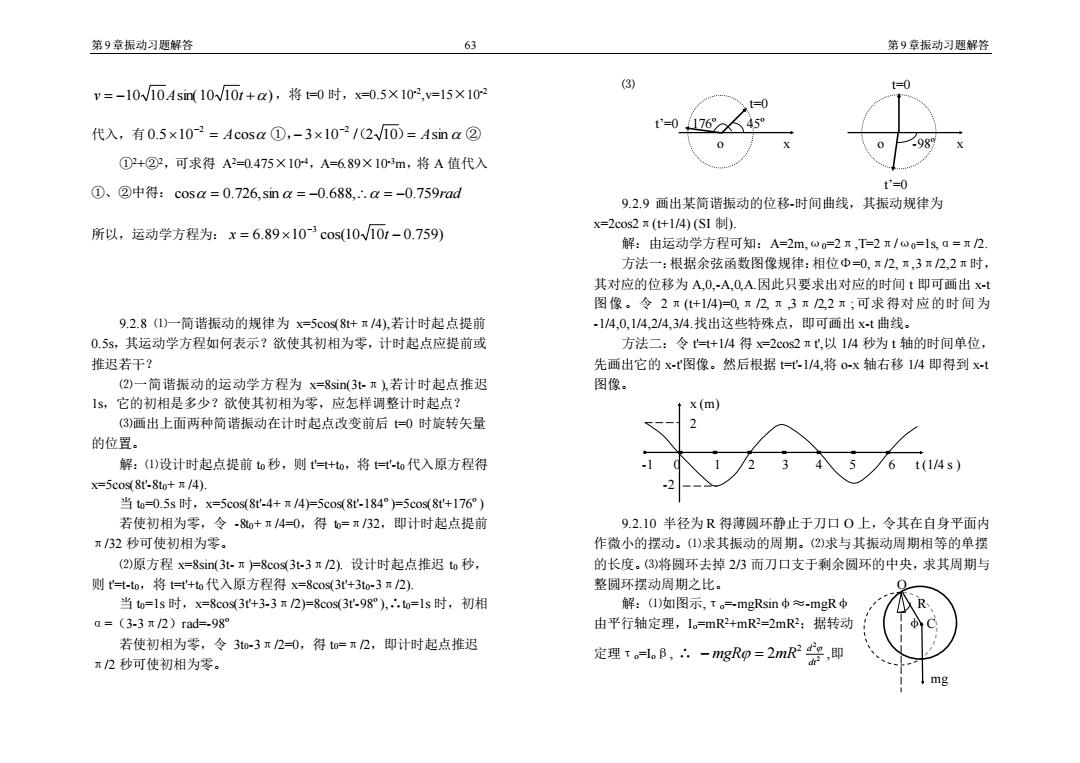
第9章振动习题解答 63 第9章振动习题解答 (3) t=0 v=-10V10Asm10W101+),将0时，x=0.5×102,v=15×102 代入，有0.5×10-2=Acosa①，-3×10-2/(2W10)=Asin a② t'=0176X 98 ①2+②2，可求得A2=0.475×10,A=6.89×103m,将A值代入 t'=0 ①、②中得：cosa=0.726,sm=-0.688,∴.a=-0.759rad 9.2.9画出某简谐振动的位移-时间曲线，其振动规律为 x=2cos2 (t+1/4)(SI ) 所以，运动学方程为：x=6.89×10-3cos10V101-0.759) 解：由运动学方程可知：A=2m,00=2,T=2r/00=1s,a=T2. 方法一：根据余弦函数图像规律：相位中=0，π2，严，3π2,2π时，其对应的位移为A,0,-A,O,A.因此只要求出对应的时间t即可画出x-t 图像。令2π(+1/4)=0，π2，π，3π22π；可求得对应的时间为 9.2.8(1)一简谐振动的规律为x=5cos8t+r/4),若计时起点提前 -1/4,0,1/4,2/4,34.找出这些特殊点，即可画出x-t曲线。 0.5s,其运动学方程如何表示？欲使其初相为零，计时起点应提前或方法二：令=+1/4得x=2cos2πt,以1/4秒为t轴的时间单位，推迟若干？先画出它的x-t图像。然后根据=-1/4，将o-x轴右移1/4即得到x-t (2)一简谐振动的运动学方程为x=8si(3t.π，若计时起点推迟图像。 1s,它的初相是多少？欲使其初相为零，应怎样调整计时起点？ X(m】 (3)画出上面两种简谐振动在计时起点改变前后=0时旋转矢量的位置。解：(1)设计时起点提前to秒，则=t+to,将=-o代入原方程得 6t(1/4s) x=5cos8t'-8to+/4). 当to=0.5s时，x=5cos(8t-4+n/4)=5cos(8t-184°=5c0s8t'+176) 若使初相为零，令-8o+π/4=0，得0=π32，即计时起点提前 9.2.10半径为R得薄圆环静止于刀口0上，令其在自身平面内 π32秒可使初相为零。作微小的摆动。(1)求其振动的周期。(2)求与其振动周期相等的单摆 (2)原方程x=8sin(3t-π=8cos3t-3π2).设计时起点推迟to秒，的长度。(3)将圆环去掉2/3而刀口支于剩余圆环的中央，求其周期与则t=t-to,将t=t+to代入原方程得x=8cos(3'+3to-3π/2). 整圆环摆动周期之比。当to=1s时，x=8co3+3-3m2)=8cos(3-98°)，to=1s时，初相解：(1)如图示，to=-mgRsin中≈-mgR中 a=(3-3r/2)rad=-98 由平行轴定理，1.=mR2+mR2=2mR2:据转动若使初相为零，令3to-3π2=0，得to=I2,即计时起点推迟 π2秒可使初相为零。定理rl,B,-mgRp=2mR空，即 ↓mg

第9章振动习题解答 63 第9章振动习题解答 v = −10 10Asin(10 10t +) ，将 t=0 时，x=0.5×10-2 ,v=15×10-2 代入，有 0.510−2 = Acos ①，− 310−2 （/ 2 10）= Asin  ② ①2+②2，可求得 A2=0.475×10-4，A=6.89×10-3m，将 A 值代入 ①、②中得： cos = 0.726,sin  = −0.688, = −0.759rad 所以，运动学方程为： 6.89 10 cos(10 10 0.759) 3 =  − − x t 9.2.8 ⑴一简谐振动的规律为 x=5cos(8t+π/4),若计时起点提前 0.5s，其运动学方程如何表示？欲使其初相为零，计时起点应提前或推迟若干？ ⑵一简谐振动的运动学方程为 x=8sin(3t-π),若计时起点推迟 1s，它的初相是多少？欲使其初相为零，应怎样调整计时起点？ ⑶画出上面两种简谐振动在计时起点改变前后 t=0 时旋转矢量的位置。解：⑴设计时起点提前 t0 秒，则 t'=t+t0，将 t=t'-t0 代入原方程得 x=5cos(8t'-8t0+π/4). 当 t0=0.5s 时，x=5cos(8t'-4+π/4)=5cos(8t'-184º)=5cos(8t'+176º) 若使初相为零，令 -8t0+π/4=0，得 t0=π/32，即计时起点提前 π/32 秒可使初相为零。 ⑵原方程 x=8sin(3t-π)=8cos(3t-3π/2). 设计时起点推迟 t0 秒，则 t'=t-t0，将 t=t'+t0 代入原方程得 x=8cos(3t'+3t0-3π/2). 当 t0=1s 时，x=8cos(3t'+3-3π/2)=8cos(3t'-98º),∴t0=1s 时，初相 α=（3-3π/2）rad=-98º 若使初相为零，令 3t0-3π/2=0，得 t0=π/2，即计时起点推迟 π/2 秒可使初相为零。 ⑶ t=0 t=0 t’=0 176º 45º o x o -98º x t’=0 9.2.9 画出某简谐振动的位移-时间曲线，其振动规律为 x=2cos2π(t+1/4) (SI 制). 解：由运动学方程可知：A=2m,ω0=2π,T=2π/ω0=1s,α=π/2. 方法一：根据余弦函数图像规律：相位Φ=0,π/2,π,3π/2,2π时，其对应的位移为 A,0,-A,0,A.因此只要求出对应的时间 t 即可画出 x-t 图像。令 2π(t+1/4)=0,π/2, π,3π/2,2π;可求得对应的时间为 -1/4,0,1/4,2/4,3/4.找出这些特殊点，即可画出 x-t 曲线。方法二：令 t'=t+1/4 得 x=2cos2πt',以 1/4 秒为 t 轴的时间单位，先画出它的 x-t'图像。然后根据 t=t'-1/4,将 o-x 轴右移 1/4 即得到 x-t 图像。 x (m) 2 -1 0 1 2 3 4 5 6 t (1/4 s ) -2 9.2.10 半径为 R 得薄圆环静止于刀口 O 上，令其在自身平面内作微小的摆动。⑴求其振动的周期。⑵求与其振动周期相等的单摆的长度。⑶将圆环去掉 2/3 而刀口支于剩余圆环的中央，求其周期与整圆环摆动周期之比。 O 解：⑴如图示,τo=-mgRsinφ≈-mgRφ R 由平行轴定理，Io=mR2+mR2=2mR2；据转动 φ C 定理τo=Ioβ, ∴ 2 2 2 2 dt d mgR mR  −  = ,即 mg

第9章振动习题解答 64 第9章振动习题解答安+条p=0∴0。=√条，T=恶=2π四 1=m12+m,h2,代入(1)中T=2π 22+3h2) 3g2h+1) ②：单摆的周期为T=2π，√厂“与薄圆环振动周期相等的单摆的摆长L=2R (3)设剩余圆环的质心在c处，质量为 ①当1=1mh=0.5m时，云=√20益 2+3x0.52 ≈0.9354 m/3.据平行轴定理：1。=l+mr23;l。=mR23 2+≈1.155 =l+m(R-r)2/3,∴.l=mR2/3-m(R-r)2/3=2mRr/3-mr2fe 当1e1mhm时，云= 代入前式得1。=2mRr/3.设余环摆角为中，则 2)令T=To,即12+3h2=12+2hl,h(3h-2)=0,解得： t。=-mgr中/3.由转动定理t。H.B。,有-mgr中/3=(2mRr/3)d2中/df, 即产+条中=0，∴0，=√景，T=总=2π√臣，由于和剩余环的 h=0.h=2/3 在=0处加小物体，即把物体放在转轴处，对摆的摆动毫无影大小无关，可知，无论剩余环多大，只要刀口支于剩余环的中央，其振动周期就和整个圆环的振动周期相等。响，故周期不变。由T。=2π√可知，此物理摆的等效单摆长度为 I,因此，在h=I处加小物体，相当于只增加单摆的质量，没有 9.2.111m长的杆绕过其一瑞的水平轴作微小的摆动而成为物理摆。另一线度极小的物体与杆的质量相等，固定于杆上离转轴为改变单摆的长度，故周期不变。的地方。用T表示未加小物体时杆子的周期，用T表示加上小物体以后的周期。(1)求当h=50cm和h=100am时的比值TTo.(2)是否存在 9.2.12天花板下以0.9m长的轻线悬挂一个质量为0.9kg的小某一h值，可令T=To,若有可能，求出h值并解释为什么h取此值时球。最初小球静止，后另一质量为0.1kg的小球沿水平方向以1.0ms 周期不变。的速度与它发生完全非弹性碰撞。求两小球碰后的运动学方程。解：为简便起见，借用9.2.1题中求得的结果，物理摆的周期解：设m1=0.9kg,m2=0.1kg碰前m2的速度 T=2π√效()，其中h为摆质心到转轴的距离。为20=1.0m/s碰后两球的共同速度为%.由动量守恒，有m2'20=(m1+mo 未加小物体时：m=m,1=古m。2+m()子=m,1户 %==品=0.lm/s m2 v20 mi h=,代入(1)中T。=2π√ Vo 碰后两球构成一个单摆，圆频率0。=√停=√器≈3.3.设运动加小物体后：m=2mo,h=(m,h+m)/2m。=受+，学方程x=Acos(3.3t+m)(1),v=鲁=-3.3Asn3.3t+a)(2)

第9章振动习题解答 64 第9章振动习题解答 g R R g R o g dt d o T 2 2 2 2 2 0, , 2 2       + =  = = = ⑵∵单摆的周期为 g L T = 2 ∴与薄圆环振动周期相等的单摆的摆长 L=2R. o ⑶设剩余圆环的质心在 c 处，质量为 r m/3.据平行轴定理：Io=Ic+mr2 /3;Io’= mR2 /3 =Ic+m(R-r)2 /3,∴Ic=mR2 /3-m(R-r)2 /3=2mRr/3-mr2 /3 代入前式得 Io=2mRr/3. 设余环摆角为φ，则 τo= - mgrφ/3.由转动定理τo=Ioβo，有 –mgrφ/3=(2mRr/3)d2φ/dt2 , 即 g R R g R o g dt d o T 2 2 2 2 2 0, , 2 2       + =  = = = . 由于和剩余环的大小无关，可知，无论剩余环多大，只要刀口支于剩余环的中央，其振动周期就和整个圆环的振动周期相等。 9.2.11 1m 长的杆绕过其一端的水平轴作微小的摆动而成为物理摆。另一线度极小的物体与杆的质量相等，固定于杆上离转轴为 h 的地方。用 T0 表示未加小物体时杆子的周期，用 T 表示加上小物体以后的周期。⑴求当 h=50cm 和 h=100cm 时的比值 T//T0.⑵是否存在某一 h 值，可令 T=T0,若有可能，求出 h 值并解释为什么 h 取此值时周期不变。解：为简便起见，借用 9.2.1 题中求得的结果，物理摆的周期 2 (1) mghc I T =  ，其中 hc为摆质心到转轴的距离。未加小物体时： 2 3 0 2 1 0 2 2 12 0 1 0 m m , I m l m ( ) m l l = = + = 2 l hc = ，代入（1）中 g l T 3 2 0 = 2 . 加小物体后： 0 0 0 2 0 2 4 2 , ( )/ 2 l h l m = m hc = m h + m m = + ， 2 0 2 3 0 1 I = m l + m h ,代入（1）中 3 (2 ) 2( 3 ) 2 2 2 g h l l h T + + =  ∴ l hl l h T T 2 3 2 2 2 0 + + = ⑴当 l=1m,h=0.5m 时， 0.9354 1 2 0.5 1 1 3 0.5 2 2 2 0 =  +   +  T T 当 l=1m,h=l=1m 时， 1.155 1 2 1 1 1 3 1 2 2 2 0 =  +   +  T T ⑵令 T=T0 ，即 3 2 , (3 2 ) 0 2 2 2 l + h = l + hl h h − l = ，解得： h=0, h=2l/3. 在 h=0 处加小物体，即把物体放在转轴处，对摆的摆动毫无影响，故周期不变。由 g l T 3 2 0 = 2 可知，此物理摆的等效单摆长度为 l 3 2 ，因此，在 h l 3 2 = 处加小物体，相当于只增加单摆的质量，没有改变单摆的长度，故周期不变。 9.2.12 天花板下以 0.9m 长的轻线悬挂一个质量为 0.9kg 的小球。最初小球静止，后另一质量为 0.1kg 的小球沿水平方向以 1.0m/s 的速度与它发生完全非弹性碰撞。求两小球碰后的运动学方程。解：设 m1=0.9kg,m2=0.1kg,碰前 m2 的速度为 v20=1.0m/s,碰后两球的共同速度为 v0.由动量 l 守恒，有 2 20 1 2 0 m v = (m + m )v v m s m m m v 0.1 / 0.9 0.1 0.1 1.0 0 1 2 2 2 0 = = = +  + m2 v20 m1 碰后两球构成一个单摆,圆频率 3.3 0.9 9.8 0 = =  l g  .设运动学方程 x = Acos(3.3t +) (1), v = = −3.3Asin( 3.3t +) (2) dt dx c R o' v0 o x

第9章振动习题解答 65 第9章振动习题解答将t=0时，x=0,v=0.1代入，得：0=Acosa(1),0.1=-3.3 Asin a(2) 9.2.14质量为200g的框架，用一弹簧悬挂起来，使弹簧伸长 a要同时满足(1)(2)，只有取a=.π2：代入(2)得A≈0.03. 10cm,框架下方有一质量为20g的小球竖直向上飞来，与框架发生完全弹性碰撞，已知小球碰前速度为10ms,求碰后框架的运动学方所以运动学方程为：x=0.03c0s(3.3t-受) 程。解：以框架平衡位置为坐标原点，据题意： 92.13质量为200g的框架，用一弹簧悬挂起来，使弹簧伸长 10cm,今有一质量为200g的铅块在高30cm处从静止开始落进框架， k=0.2×9.810.1=19.6,00=V==√2=9.9 求铅快落进框架后的运动学方程。设小球质量为m',小球碰前速度为o,小球碰后速解：设a为弹簧自由伸长时框架的位置，度为V,框架碰前静止，碰后速度为o b为碰前框架的平衡位置，0为碰后平衡位置由动量守恒：m。'=m%+mp,由牛顿碰撞公式：Vo-v'=V。并取作坐标原点。据题意： a m ab=0.1m,k=mg/ab=0.2×9.8/0.1=19.6N/m, 6 在o点，2mg=k(ab+bo),bo=2mg/k-ab=0.1m 0 由此可求得：6=警=00=-兽≈-182ml小设碰后铅块与框架获得的共同速度为V,由动设运动学方程x=Acos(9.91+a),v=-9.9Asn(9.91+) 量守恒：m2gh=2m,V=√2g动12=√2×9.8×0.3/2≈1.21 代入初始条件：0=Acosa①，-1.82=-9.9Asna② 碰后框架与铅块振动的圆频率0。=√质=√器=7，设振动由①知a=±r2,为满足②式，取a=π/2，代入②得：A=0.184 的运动学方程为x=Acos(7t+a),v=-7Asin(7t+a),将振动所以，运动学方程为：x=0.184c0s(9.91+) 的初始条件：=0时，x=0.1,v=v=1.21代入，有： 9.2.15质量为m的物体自倾角为9的光滑斜面顶点处由静止而 -0.1=Acosa①，1.21=-7 Asin a,即-0.173=Asin② 滑下，滑行了I远后与一质量为m'的物体发生完全非弹性碰撞。m 与劲度系数为k的轻弹簧相连。碰撞前m'静止于斜面上，如图所示。 ①2+②2，得：A2=(-0.1)2+(-0.173)2≈0.04，A=0.2m,将A 问两物体碰撞后作何种运动，并解出其运动学方程。已知m=m'=5kg, k=490N/m,0=30°，=0.2m 值代入①、②中得：cosa=-0.5,sina=-0.865,a=-120°=-2π/3 解：设a为弹簧自由所以，运动学方程为：x=0.2C0s(7t-号π) 伸长处，b为只有m时的平衡位置，o为m与m'粘在一起时的平衡位置.以o 为原点，建立图示0x坐

第9章振动习题解答 65 第9章振动习题解答将 t=0 时,x=0,v=0.1 代入,得：0=Acosα ⑴’, 0.1= - 3.3Asinα ⑵’ α要同时满足⑴’ ⑵’，只有取α=-π/2；代入⑵’得 A≈0.03. 所以运动学方程为： 0.03cos(3.3 ) 2  x = t − 9.2.13 质量为 200g 的框架，用一弹簧悬挂起来，使弹簧伸长 10cm，今有一质量为 200g 的铅块在高 30cm 处从静止开始落进框架，求铅快落进框架后的运动学方程。解：设 a 为弹簧自由伸长时框架的位置， b 为碰前框架的平衡位置，o 为碰后平衡位置并取作坐标原点。据题意： ab=0.1m, k=mg/ab=0.2×9.8/0.1=19.6N/m, 在 o 点，2mg=k(ab+bo), bo=2mg/k-ab=0.1m 设碰后铅块与框架获得的共同速度为 v'，由动量守恒: m 2gh = 2mv' ,v' = 2gh / 2 = 29.80.3 / 2 1.21 碰后框架与铅块振动的圆频率 7 2 0.2 19.6 0 2 = = = m   k ，设振动的运动学方程为 x = Acos(7t +), v = −7Asin( 7t +) ，将振动的初始条件：t=0 时, x = -0.1, v = v'=1.21 代入，有： −0.1= Acos ①，1.21= −7Asin,即−0.173 = Asin ② ①2+②2，得： A ( 0.1) ( 0.173) 0.04, A 0.2m 2 2 2 = − + −  = ，将 A 值代入①、②中得：cosα= -0.5, sinα= -0.865, α= -120°= -2π/3 所以，运动学方程为： 0.2cos(7 ) 3 2 x = t −  9.2.14 质量为 200g 的框架，用一弹簧悬挂起来，使弹簧伸长 10cm，框架下方有一质量为 20g 的小球竖直向上飞来，与框架发生完全弹性碰撞，已知小球碰前速度为 10m/s，求碰后框架的运动学方程。解：以框架平衡位置为坐标原点，据题意： 0.2 9.8/ 0.1 19.6, 9.9 0.2 19.6 =  = 0 = = = m k k  设小球质量为 m'，小球碰前速度为 v0'，小球碰后速度为 v'，框架碰前静止，碰后速度为 v0 由动量守恒： ' ' ' ' 0 0 m v = mv + m v ，由牛顿碰撞公式： ' ' 0 0 v − v = v 由此可求得： v m s m m m v 1.82 / 11 20 0.2 0.02 2 0.02 ( 10) ' 2 ' ' 0 0 = = = −  − +   − + 设运动学方程 x = Acos(9.9t +), v = −9.9Asin( 9.9t +) 代入初始条件： 0 = Acos ①， −1.82 = −9.9Asin ② 由①知α=±π/2，为满足②式，取α=π/2，代入②得：A=0.184 所以，运动学方程为： 0.184cos(9.9 ) 2  x = t + 9.2.15 质量为 m 的物体自倾角为θ的光滑斜面顶点处由静止而滑下，滑行了 l 远后与一质量为 m’的物体发生完全非弹性碰撞。m’ 与劲度系数为 k 的轻弹簧相连。碰撞前 m’静止于斜面上，如图所示。问两物体碰撞后作何种运动，并解出其运动学方程。已知 m=m’=5kg, k=490N/m,θ=30º,l=0.2m. 解：设 a 为弹簧自由 m 伸长处，b 为只有 m’时的 a m’ 平衡位置, o 为 m 与 m’粘 b k 在一起时的平衡位置.以 o O θ 为原点，建立图示 o-x 坐 x a m b m o x m' m v0' o x

第9章振动习题解答 66 第9章振动习题解答标。由平衡条件有： m' g sin  = kab, (m + m')g sin  = kao . ob = ao − ab = mg sin  / k = 59.8 0.5/ 490 = 0.05m 设 m 与 m’碰前速度为 v1，由能量守恒， 2 2 1 1 mglsin = mv ， v1 = 2glsin  = 29.80.20.5 =1.4 .设 m 与 m’碰后共同速度为 v0,由动量守恒 mv m m v v m s v m m mv ( ') , 0.7 / 1 0 0 2 1 ' 1 = + = = = + 显然，碰撞后两小球在平衡位置 o 附近作简谐振动，其圆频率 7 2 5 490 0 2 = = = m   k . 设运动学方程为 x = Acos(7t +) （1），速度 v = = −7Asin( 7t +) (2) dt dx . 将初始条件 t = 0, x = −0.05， v = 0.7 代入得： − 0.05 = Acos (1)', 0.7 = −7Asin  (2)' . 可解得：A=0.1118m,α= - 1.107rad..∴ x = 0.1118cos(7t −1.107) 9.3.1 1851 年傅科作证明地球自转的实验，摆长 69m,下悬重球 28kg.设其振幅为 5.0º，求其周期和振动的总能量，重球最低处势能为零。解： T s g l 2 2 3.14 16.7 9.8 69 =  =   ；根据能量守恒，振动的总能量等于摆在最高点时的势能 E mgl(1 cos ) 28 9.8 69(1 cos5 ) 72 j = −  max =   −   9.3.2 弹簧下面悬挂质量为 50g 的物体，物体沿竖直方向的运动学方程为 x=2sin10t,平衡位置为势能零点（时间单位：s,长度单位； cm）.⑴求弹簧的劲度系数，⑵求最大动能，⑶求总能。解：⑴∵ m k , k m 0.05 10 5N / m 2 2 0 2 0 =  =  =  = ⑵∵ v t v cm s m s dt dx 20cos10 , 20 / 0.2 / = =  max = = E mv j k 2 2 3 2 max 1 max 0.5 0.05 0.2 1.0 10− = =   =  ⑶根据能量守恒，总能量等于最大动能，为 1.0×10-3 j 9.3.3 若单摆的振幅为θ0，试证明悬线所受的最大拉力等于 mg(1+θ0 2 ) 证明：单摆的运动学方程为： cos( )  = 0 0 t + 角速度 / sin( )  = d dt = −0 0 0 t + 在法向方向应用牛顿第二定律： cos sin( ) cos 0 2 0 2 0 2        = + + − = = T mg ml t T mg ma m l n 0 2 2 0 5 , cos 1, ,         =  t + = l g  时，T 最大所以， (1 ) 2 0 2 Tmax = mg + mg 0 = mg + 9.4.1 在电子示波器中，由于互相垂直的电场的作用，使电子在荧光屏上的位移为 x = Acosωt, y = Acos(ωt+α).求出α=0，π/3， π/2 时的轨迹方程并画图表示。 y 解：⑴α=0 时，轨迹方程 y=x,如图 a 所示。 ⑵α=π/3 时， x = Acosωt, 0 x y = Acos(ωt+π/3)= A(cosωt cosπ/3 – sinωt sinπ/3) mg θ T n τ

西安电子科技大学：《大学物理》课程习题解答（力学）第9章 振动习题解答

西安电子科技大学：《大学物理》课程习题解答（力学）第9章振动习题解答