
第十一章恒定电流的磁场 44e (一)磁感应强度毕一萨定律及应用 一、选择题与填空题: 1.一圆电流在其环绕的平面内所包围区域各点的磁感应强度阝: (A)方向相同,大小相等; (B)方向不同,大小不等: (C)方向相同,大小不等: (D)方向不同,大小相等。 2.电流由长直导线流人一电阻均匀分布的金属矩形柜架,再从长直导线流出,设图中 0、02、0处的磁感应强度为1,B2,B,则: (A)B1=B2=B2=0 (B)B1=2=0,B,≠0 (C)B1=0,B2≠0,B,=0 (D)B1=0,B2≠0,B3≠0 02 03 3.边长为L的一个导体方框上通有电流I,则此框中心的磁感应强度 (A)与L无关; (B)正比于L2; (C)与L成正比; (D)与L成反比 (E)与P有关。 4.如图两个半径为R的相同的金属环在a、b两点接触(a、b连线为环直径),并相互垂 直放置,电流I由a端流人,b端流出,则环中心0点的磁感应强度大小为: (A) (A)0 (B) 4R o验 ·16:
第:十 ˉ章∷∷恒定屯`流∷的磁场 毕ˉ萨定 ∷ 律及应用 1.一 圆电流在其环绕的平面内各点的磁感应强度 茁: (A)方 向相同,大小相等; ∷ (B)方 向不同,大小不等; ∷∶∷.∷ (C)方 向相同,大小不等; Ⅱ ∶ (D)方 向不同,大小相等。 2.电 流由长直导线流人一电阻均匀分布的金属矩形柜架,再从长直导线流出,设 图中 ˉ · ·ˉˉˉˉˉ |∶ ∶∶∶∶∶∶∶∶∶∶∶||ˉ ˉ ,.· ˉ 厂 ˉˉ ~ Ⅰ~I~ ェ 3.边长为 L的∷个导体方框上通有电流 I,则此框中心的磁感应强度 ∷ (A)与 L无关; (B)正 比于 ′; (C)与 L成正比; (D)与 L成反比 (E)与 ′有关。 4.如 图两个半径为 R的相同的金属环在 a、 b两点接触 帚 径 ),牙 谔屑 直放置 ,电 流 I由 a端流人 ,b端流出,则环中心 0点 的磁感压 莺 (一 )磁 感应强 j度 一、选择题与填空题: 01、 02、 03处的磁感应强度为j1j2j3,贝刂: (A)B1亠 B2〓 B3=0 (C)B1〓 0, B2≠ 0, B3=o (A)0 (B)措 泅架 ⑼譬 (B)j1亠 Bz=0, 言3≠ o (D疒言1〓 盯瓦乒0,言3≠ o C○ (~∶ !;丨 ) (~!∶ ))) ·16·
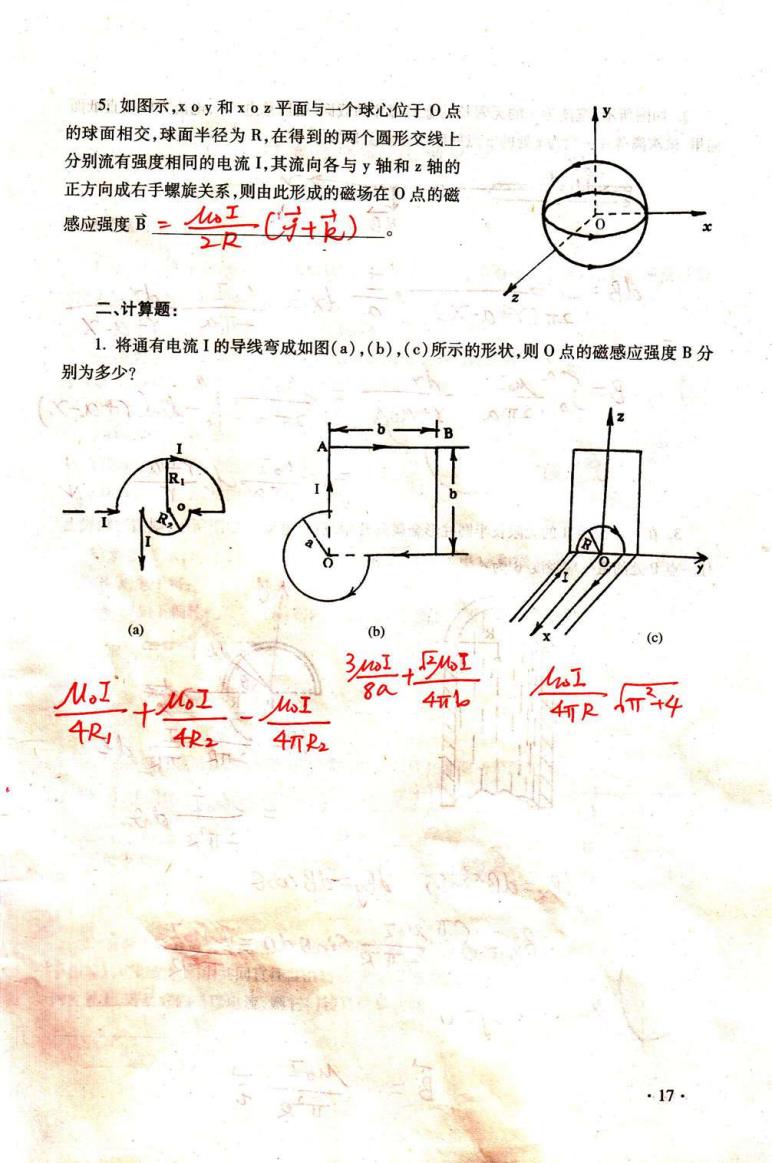
5.如图示,x0y和x0z平面与一个球心位于0点 y 的球面相交,球面半径为R,在得到的两个圆形交线上 离水女果 分别流有强度相同的电流I,其流向各与y轴和z轴的 正方向成右手螺旋关系,则由此形成的磁场在O点的磁 感应强度B二(时+) 二、计算题: 1. 将通有电流I的导线弯成如图(a),(b),(c)所示的形状,则0点的磁感应强度B分 别为多少? B (b) (c) W.1 M 4m6 何尺行+4 4机P2 ·17
∷Ⅱ玎∵如图示,x∶ 9i和 xo'平面与△个球心位∷于ρ点 的球面相交,球面半径为R,在得到的两个圆∷形交线上 分别海有强度相同的电流I,其 流向各与∮轴釉立轴的 正方向成右手螺旋苯系,则 由此形成的磁场在p点的磁 蒽应娘度∷j三 型丝墨三E星⊥宝‘ 、∷∵ ˉ 二、计算题: ∷ ∴ ∴Ι r 1.将通有电流I的导线弯成如图(a),(b),(c)所示的形状,则 o点 的磁感应强度 B分 别为多少? ∶ =△∴∷ ● , 彡”Ⅱ工∷ 衍 :厶 爹啭 而 迦 篑∷ ∶ :唣 。 : iF夂 ∷ 钶 肛 · `.∷ ' 7∶|亨∶蚤了0 ∷Ⅱ .Ⅱ ∶∶∶i∷ ∶∶:皂熏营宫壬:|∶ 17·

2.如图所示,宽度为a的无限长的金属薄片的截面,通以总电流I,电流方向垂直纸面 向里,试求离薄片一端为r处的P点的磁感应强度B为: 加交群面总国 【张中的同出林端设 能,关道学年计英词面 》一是童明 8ax吾k 以 2兀& Yta-x B=01 会点Crta刘 领以↓ 3.在一半径为R的无限长半圆柱形金属薄片中,通有电流I,如图所示,则圆柱轴线上 任一点P处的磁感应强度B为: R 8 最最北 .工dd 2切次 dB=desine,My-dBo Bx7m90= T22 By-o ·18·
2.如 图所示,宽度为 a的无限长的金属薄片的截面j通 以总电流 I,电 流方向垂直纸面 向里,试求离薄片△端为r处 的p点 的磁感应强度 B为△∷∶∶△∷ Ⅱ == ∷·∷¨ 0 9-∵ ∷ 沈B I∷ ∷ ∶ 1∷ェ :∷ ∷ △ ∷ 忄 豸冗瓦Γ ·丢加·z壅~丛辶 ∷ Dcta rt犹 △刃 旰觅旰 缶 F绎h汛而 ∷ △《箅知毛厶 :辱⒐ ↓ 3.在△半径为 R的无限长半圆柱形金属薄片中,通有电流 I,如 图所示,则 圆柱轴线上 任工点P处的磁感应强度言为: 刃£妊:柔 加 吖篝桫 ·18· 茄民=仄B臼昭'钧 叫 罕冖 0 民ˉ¢纬 。Ⅱ F禽 刊氵彡o 3亠 ∠吐~刂 丨1\∶ 刂∵

单洋甘聊轮华部流提否出视发香由甚格医静游的单饭国: 单将膏 费酒 (二)毕一萨定律应用(续)、高斯定理 一、选择题与填空题 1.四条相互平行的载流长直导线,电流强度均为L,且垂直于纸面,如图放置,正方形的 边长为2a,则正方形中心0的磁感应强度应为: ‘○ (A)B=21 Ta (B)B=24 02a (C)B=0 00 (D)B=1 2.一卉口曲面如图,开口是半径为R的圆,匀强磁场B与开口圆所决定平面的内法线 方向的夹角为0,通过这个曲面的磁通量为 (A)0 (B)-TR2Bcos0 (C)πR2Bcos0 (D)TR Bsin0 3.如图有六根无限长导线互相绝缘,通过电流均为L,区域I、Ⅱ、Ⅲ、Ⅳ均为面积相等 的正方形,问: 事资,书长闻,P庆开折泌生过 个 个 :、,应端收法和,火演国进明心示品减少的 2 之-。一A(逃礼两开代 :是分中慰酒《S (A)通过区域 工V的磁通量为零。 A (B)通过区域亚指向纸外的磁通量最大。 (C)通过区域立指向纸内的磁通量最大。 4. 电量为q的带电粒子以角速度ω作半径为R的匀速率圆运动,在圆心处产生的磁 感应强度B= 九。w .12 杯P
∷∷ ∷∷∷∷∷∴∷∵∷∷ 0Ⅱ∷ ∷∷△∷ ∷∶ ∷Ⅱ∷ ∷∵∷△~ ∴∷ ∷ ∷言: ∷ Ⅱ亭 ∵ `l (二)毕 ∵萨定律应用(续 )(高 斯∴定理: -t选择题与填空题: 1.四条相互平行的载流长直导线,电流强度均为I,且垂直于纸面,如 图放置,正方形的 边长为 za,贝刂正方形中心 o的磁感应强度应为: (D (A)B〓 ⒉型L1 πa 山:|篇 ∷ 、| (C)B_o ∷ . ∷ = ^ ` ∷ .∷ ∷Ⅱ∷∶∶ |i∴ ∷∴∷ ∷∶∶ ∶ = 早:虍呷 乌 (A)0 (B)亠 πR2Boosθ (C)πR2Bcosθ (o)π |口 R2Bsinθ 早咛肀艺 3.如图有六根无限长导线互相绝缘,通 过电流均为 I,区域 I、 Ⅱ、Ⅲ、Ⅳ均为面积相等 的正方彤,问 Ⅱ ∷ Ⅱ∶∷ˉ∷∴∵∷∵Ⅱ ∵Ⅱ `;: (^)通过区域 △ J/m磁通量为氛 ˉ i| 彗最大。 啻最大。 半径为 R的匀速率圆运动,在 圆心处产生的磁

才5. 半径为R的细圆环均匀带电,电荷线密度为入,若圆环以角速度。绕通过环心并垂 直于环面的轴匀速转动,则环心处的磁感应强度B。二子轴线上任一点的磁感应强度 B= 从R3 2C须+x万 年讲丝州而泸证 二、计算题和证明题: 1.如图所示,载流无限长直导线电流【,与直线共面的矩形面积和三角形面积的磁通量 分别为多少?于 a) b 6 a ←a I cb-am) 其距四密细 2.两根长直导线沿半径方向连接到粗细均匀的铝环上A、C两点,导线的另外两端与很 远的电源相连接,试证明“无论A、C两点在圆环上何处,环心O处的磁感应强度恒为零。 I14=12 0- 工 Ri ® B2:o12 4πk2 ⊙ B32B430 B20 ·13·
卜 半径为 R的细圆环均匀带电,电荷线密度为λ,若 圆环以角速度 0绕通过环心并垂 面的轴匀速转动,则 环心处的磁枣瘅弭擘 ∷Bo△圭2口步狲线上任=点的磁感应强度 0〓~ ∴ ∷∷∷ ∷ ∷∷ ∵ 氢线共面的矩形面积和三角形面积的磁通量 - ∶△ · \~⊥ Ⅱ ∵∷ ∷「l|∷ △ 耔十?丿 ∷Ⅱ∵ ∷ 均匀的铝环上 A、 C两点,导线的另外两端与很 l环上何处,环心 0处的磁感应强度恒为零。 冫/o工∷记 (∶ ∶∶∷茹 T疝廴 9t+L ~∶|π 卜 七 .=Ⅱ “ Ⅱ沙昔。 主rˉeI二 ェP以,∴ ∷ 即钎年 @ B冫 ~'饨 王∷∶ˉe. +T托冫 B3亠 ‰二刁 B¨ 0 ·13·

杉3X霜细直线AB,电荷线密度为入绕垂直于直线的轴0以角速度。匀速转动, 线形状不变,O点在AB延长线上)求O点的磁感应强度B和旋转带电线AB所形成的环 形电流的磁矩户。 d1-兴7话 o rtdr上带电 4T Adr R-冲=女 B-JaB= Lcatba] 02 (X年)Ξ r 4电流均匀地流过宽为2a的无限长平面导体薄板(板厚可略去不计),电流强度5元 通过板的中线并与板面垂直的平面上有一点P,P到板的垂直距离为y,如图所示,求P点的 磁感应强度B。 d虹-ia 2 dB dB≥.d边 MoIdx 起 4Tar B-SdBx=-SdBcoso 【o【oo60o十→X ←2a- 4Ta酚 9京 Hatxy 14 B=_
鼬 直线 1B,电荷线密度为λ绕垂直于直线的轴0以 角速度 ω匀速转动, ˇ `a ˉ ˇ 久 △… 叮 cJ〃 叨 ∷¨ ∷ ( ∷∷ ∶∷∷ 钅轩么华 J }`⌒亻劝`=£Ψ / 在 鸶 a∥‰bl ∵ ^J吖 ′丁J河 虍 舞 λ加 (线形状 霭克:F年 A:延苌纾 上)球 0点 的 【 感应强 秽 垂鸟黟繁::所彤冖即下 鼠 `冗:丝笋 ·召争 λ尻 ' P,P到 海体薄竣‰£豕荮葚r椠右,屡纛鸶篝 板的垂直距离为 y,如 图所示 ,求 P点的 ~以 〃 h 7 呷γ `∴ ∷∴Ⅱ∵~了 二石萨 i \ 弑 浇纭 ⊥ 一 彡招 幼j汪 I∶ 一‰ 祭 r久 ^ 钎 a⒅ V 一绎 呐 贪 ·14· ° 亠 〓冫 二 D幻 丿8 衤 0 -⒛ 颀 售争师妫争
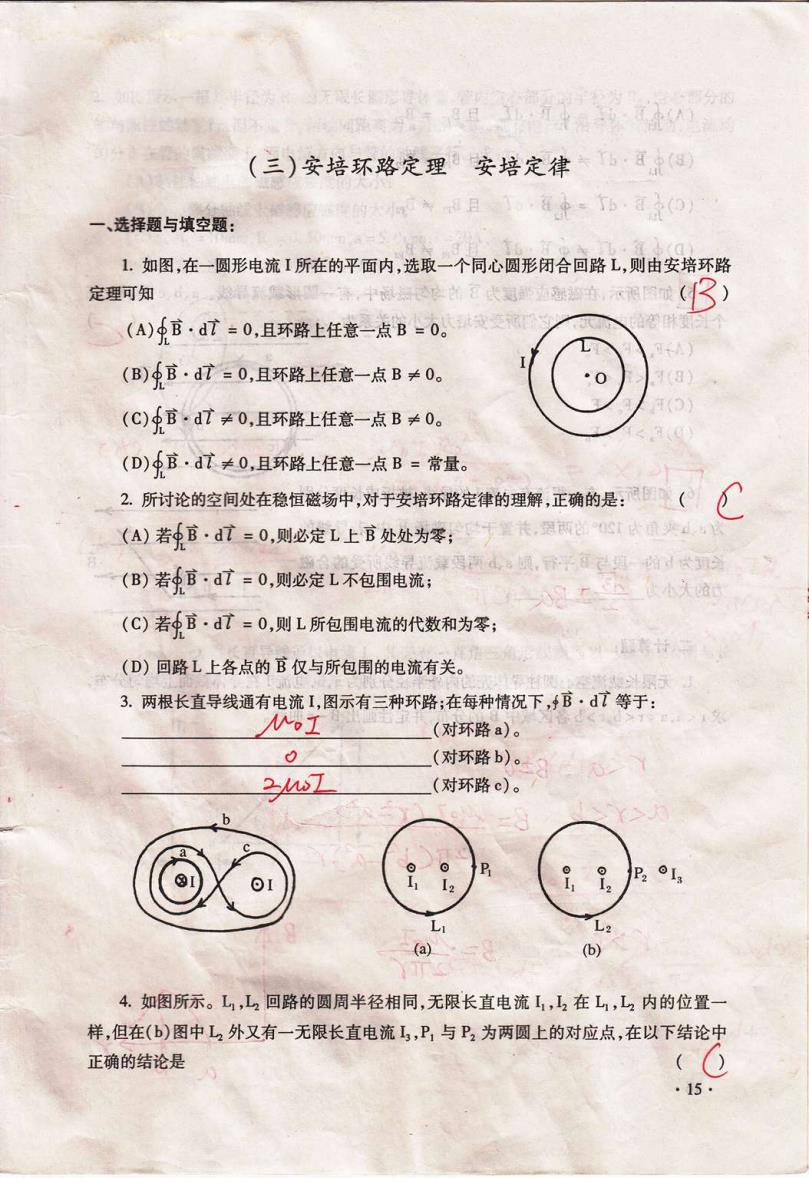
(三)安培环路定理安培定律 一、选择题与填空题: 1.如图,在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路 定理可知 中 的冠武司边缺语年,衣限的碳 3) (A)B·dt=0,且环路上任意-点B-0。发 (B)官·dt=0,且环路上任意-点B≠0。 ·0 (C)B,dt≠0,且环路上任意-点B≠0。 4(0 (D)少B·dt≠0,且环路上任意一点B=常量。 2 2.所讨论的空间处在稳恒磁场中,对于安培环路定律的理解,正确的是:( C (A)若官·d广=0,则必定L上官处处为零;天t,宽颗S类 年遇两4。顷,后平其的d代切 (B)若B·dt=0,则必定L不包围电流; (C)若官·dt=0,则L所包围电流的代数和为零; (D)回路L上各点的B仅与所包围的电流有关。 3.两根长直导线通有电流1,图示有三种环路;在每种情况下,B·dT等于: MoI (对环路a)。 0 (对环路b)。 2w7 (对环路c)。 (a) (b) 4.如图所示。L,L2回路的圆周半径相同,无限长直电流1,2在L,L2内的位置一 样,但在(b)图中L2外又有一无限长直电流L3,P,与P2为两圆上的对应点,在以下结论中 正确的结论是 ·15·
(三 )安培环路定理 安 培定律 ∷ 一、选择题与填空题: 1.如 图,在一圆形电流 I所在的平面内,选取一个同心圆形闭合回路 L,则 由安培环路 定理可知 ∷ (A)虫 j· 。σ 〓0,且环路上任啬一 点 o=o。 (:)兑官·d氵 〓0,且坏路上任意⊥点 B≠ 0。 I (C)兑言。d氵 ≠0,且环路上任意一点 B≠ 0。 (D)兑 官·d氵 ≠0,且坏路上任意一点 B〓 常量。 (B) 2.所讨论的空间处在稳恒磁场中,对于安培环路定律的理解,正确的是: ( (|)若∮ 言·d氵 〓0,则必定 L上 言处处为零; (B)若虫 言·J=0,贝刂必定 L不包围电流; (C)若虫 言·d氵 〓0,则 L所包围电流的代数和为零; (D)回 路 L上各点的言仅与所包围的电流有关。 3.两根长直导线通有电流 I,图示有三种环路;在每种情况下,∮ 言·d氵 等于 '伊 讠ェ (对环路a)。 (对环路b)。 ; 冖 (对环路 c)。 △ °凡 4.如 图所示。L1,△ 回路的圆周半径相同,无 限长直电流 I1,I2在 L1,△ 内的位置一 样,但在(b,图 中△外又有一无限长直电流 I3,P1与 Pz为 两圆上的对应点,在 以下结论中 (((∶∶1 ·15· L2 正确的结论是

(A)4B·dt=克Bdt且Bm=Bm (B)克Bdt≠克B:dd且BeBa8( (C)克B,dt=克Bdt且Bn≠Bn 醒空欢已漫数, (D)克Bdt≠克B.dt且Bm≠Bm 的面平出许疯1前中一市,图 5 如图所示,在磁感应强度为B的均匀磁场中,有一圆形载流导线。a、b、c是其上三 个长度相等的电流元,则它们所受安培力大小的关系为1褐日.0.16·怎 (A)F.>Fb>F。 (B)F.F。>F. 0¥1款一意国 (D)F.>F.>F6 量靠8克一 6,平图所示,有一根流有电流1的导线,被折成长度分别 为a、b夹角为120°的两段,并置于均匀磁场B中,若导线的 长度为b的一段与官平行,则a、b两段载流导线所受的合磁 力的大小为是工B队· 达所度南敢中雨子俱0=中等0) 二、计算题: 1.无限长载流空心圆柱导体壳的内外半径分别为a,b,电流1在导体截面上均匀分布, 早直头球阿 求rb各区域中B的分布,并定性画出B~r曲线。 丫b B=M B个 2TY 一低过的面」,工立下,话直习架买,闻脉半明速的线西 中能不通,点统状的侧酒状志9实首鼎天 ·16
(A)藐1=· 盯=鬼言·叮 早:m=:⒓ (:)虫 =· 。氵≠凫氵:· d礻 丹:艹 :丁 卩Ⅱ∶∷∴∷ ∶ (C)虫氵 ·J=凫 言 ·f且 BH≠ ‰ ∷Ⅱ (A)F己 ≥Fb>FC (B)F。 k Fb《 F¢ (C)Fb)Fc>F3 (D)F。 >F∶∷冫Fb r>1 a、 b、 c是其上≡ (d ∷平t珏 gF9i昏 有聊 呻喜练扁山弘蚓良擘夯剔: 为 a~,b夹 角为 1⒛ °的两翠 ,并置于均匀磁场 歹屮 |荇早绋的∷ 蚤髯炎未凳二晕舅EJ歹廴|:′ b两早 载F早罕厂 F的 合磁 二、计算题: 1.无限长载流空心圆柱早铃壳的内外半在分别为 占:。 ,电流 I在导体截亩上均匀分布, 求r(轧 akr亠 1∴ ’ b查菡备补i】戒芬拜l∶并走硅画山:ti曲线。∷ ∷ r<次 ∷B冫o∶ ¢<、你L- B圭 /°△. ‘rL亡) ∷冫ⅡC∽冖Or B0绎 。16·

2.如图所示一根外半径为R,的无限长圆形导体管,管内空心部分的半径为R2,空心部分的 轴与圆柱的轴平行,但不重合,两轴间距离为a,且a>R,现有电流I沿导体管流动,电流均 匀分布在管的横截面上,而电流方向与管的轴线平行。求:。日件的题泡直清第 (A)圆柱轴线上的磁感应强度的大小; (B)空心部分轴线上磁感应强度的大小; (C)设R1=10mm,R2=0.50mm,a=5.0mm,I=20A 分别计算上述两处磁感应强度的大小。 空心部分 R CA) B=工 心oIP2 2万0 2TaCP-P3) ≥2X1a CB)B=从工,A Moa I >TRP 2TP ·.TR2-o7风 T2e3) zTC2对 o行 无限长直导线通以电流1,其旁有一直角三角形线圈通以电流↓2,线圈与长 直导线在同一平面内,尺寸如图所示,求:bc,ca两段导线所受的安培力。 Foc=MoL Ie Tcdte) 个 dF=I deg d =noZ2d儿 X >-T元 o11,-d F-∫dF=422 ≥hwL π ·17.d
2.如 图所示一裉外半径为R:的无限长圆形导体管,管内空心部分的半径为Rz,空心部分的 轴与囝拄曲Ⅱ平行,但不重合,两轴阃距离为a,且 a>曳 ,现有电流 I沿导体管流动,电流均 匀分布在甘的横截面上,而 电流方向与管的轴线平行。求: ∷∴Ⅱ =∷ ∴Ⅱ∴∴∶∷ (止)囝拄轴线上的磁感应强度的大小; (B)空心部分轴线上戒感应强度的大小; (C)i殳 R1〓 10m叩 ,Rz〓0∷⒑mⅡ ,a=5.0mm,I〓 ⒛A, Ⅱ ∶ 分别计算上述两处磁感应强度的大小。 C府) B二 '袒巫红~I 冫百 a 2丌灸己H廴艮V '‘ 。Ⅰ2亡 一‘ 》)× /DT 乙BD B=~力 嗵 止 二 冫仇。久 △丌R卩 π 蛘 ρiD 口 一无限长直导线洱以电流I:,其旁有丁直角三角形线圈通以电流疋蓖霾担魏驴 +T l 直导线在同一平面内,尺 寸如图所示 ,求 :bc,ca两 段导线所受的安培力。 hl 。'''刂 。't辽:∶∶l∶ ∶J冫 冖Γ冖1(!∶ ' 》π ul冫 .TRl) 冫 '‰ ⒕ 。Ⅱ¢I乇叫 丁 ← J Fbc二 亠T丿钐 ) 彬灬 卜 a d l▲ 丁 丨 丨 ﹂ △ x △ 丌冗 卜伽=」。∶∶:纟笔f年:|L‘ 镌 冫等
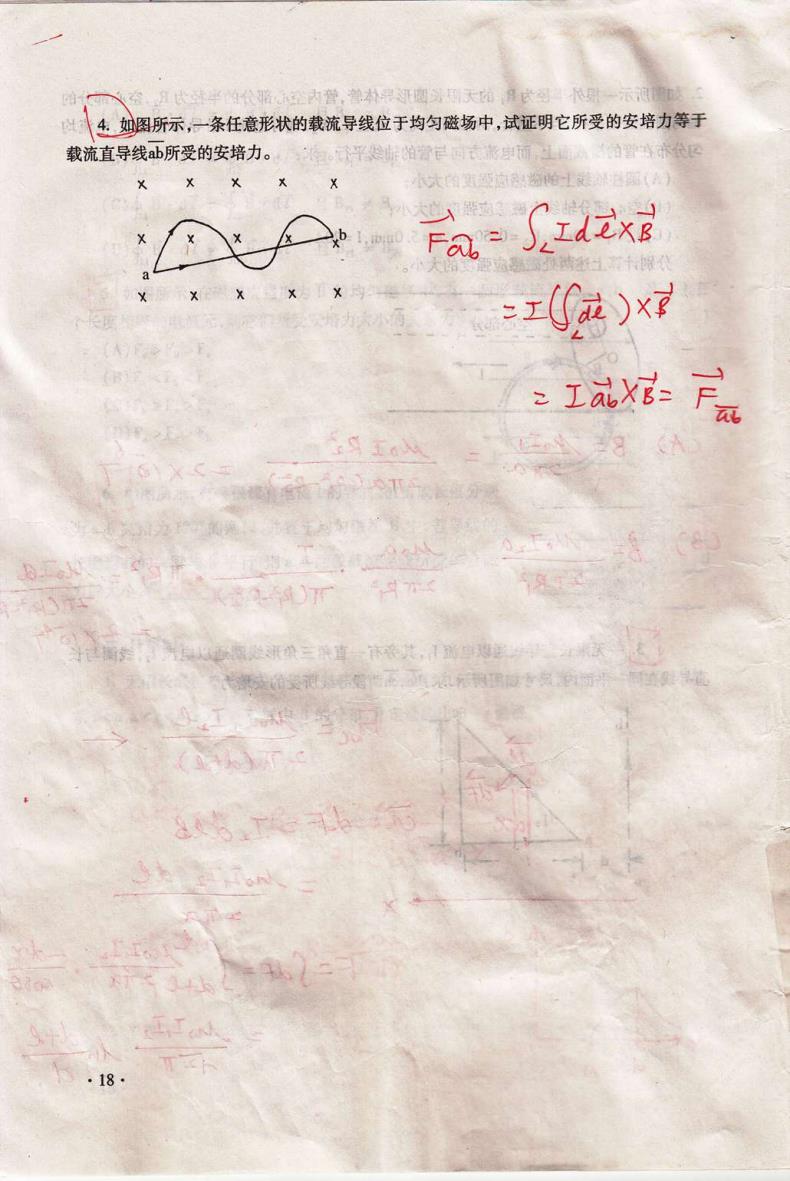
金,达平代路金内管,兽村甲圆天布月他班一示调 4.如图所示,一条任意形状的载流导线位于均匀磁场中,试证明它所受的安培力等于 载流直导线b所受的安培力。。平滑已回击能京而王动角雪平 X )X7 iX:广 月王 28A 远小5 、 ”4 幸三连菜其庆 城发前能德利明设专防单道 ( 18
o∷ |∴∴∶=∷∷∷ =Ⅱ 嵛:∷ ∶‘∶∶∶ij氵l宝k∶ 氨∴f|△ △∷ ∶∷∴ |-9瓦:「: 1… ˉ oo ∷△喊∷|∷ △ ㈡·廴瓦 一 ·∷〓 ∷\∶ 、 〓 丶 ~△ ∷ 〓! ∵^∷ ⒈ 一 ‘ ∷ ∷ `∷ ` `丶 〓 〓 Ⅰ貊 丫 ∷∶Ⅱ,` 冫〓 一∴∷ ∷〓 ⒋∷ 脚 ~ ∷ 〓〓 ∷ ∷菘〓 一 〓 、≡ .一 ^ 〓 `〓· ∶1|-∷ ∷ = 丁 `Ⅱ ′ . ∷ = △ 、:∴ 、 |∷ ∷ △ `。 ∶ ∶· ·18′ t熬 t=∷豳