
第九章气体分子运动论 (一)理想气体的压强公式温度的本质 一、选择题与填空题 1.理想气体的微观模型是有大小、,除?作蜂山发闭仙统计假设 是平负饭工,学的向各方向运动瓶这型洋。 2.理想气体状态方程的两种表达式为:?V=T 和P=nkT 3.理想气体的压强公式为P=李丝 。表明宏观量压强P是由两个微观量 的统计平均值 n·和 决定的。 4.理想气体温度T与分子平均平动动能的关系是=子工 。温度的统计意 义是大3☑乎的手动能量没 5.一容器装着一定量的某种气体,下述几种说法哪一种对? (C) (A)容器中各部分压强相等,这一状态一定为平衡态; (B)容器中各部分温度相等,这一状态一定为平衡态; (C)容器中各部分压强相等,且各部分密度也相同,这一状态一定为平衡态。 6.1大气压27℃时,一立方米体积中理想气体的分子数n24X。), 分子热运动平均平动动能兩=人.211.3'丁二。 二、计算题: 1.图中a、c间曲线是1000mol氢气的等温线,其中压强P1=4×10Pa,P2=20×10Pa, 在“负资头兰-6外水 (2)氢气在b点和d点两状态的温度,和T,.臣T(=6k3t42k 7dAT。2w7水o,37K ·44…
第九章 ∷气体分予运动论 (△ )理 想 气体 的压 强公 式温康 的本质 -、 选择题与填空题 ∷ ∴ k ⒈理想气体的微观摸型是 哆 Ⅱ假设 丙匕讪 衤嚷制 多 。 L。 理想气体众态芳程9q荫种装达式为: `/;/RT 和 ∷ P亠 hkT 。 3.理想气体的压强公式为:|扌吒 讧 。表明宏观量压强 P是由两个微观量 的统计平均值 △ 和△△Ⅰ△亠⊥__咚定的。 4.理想气体温度I与分子平均平动动能的关系是 。温度的统计意 义是~k枷姒 血 彻 豳 幽 黎 L_工 ° ∷∷冫t容带装覃丁衣旱馋苯碑每岭o下冷丹刀 艹 ∷ ∷ ∷ -c) (A)容器中各部分压强相等,这△状态一定为平衡态Ⅱ∷∷∷ Ⅱ∷∷∷∷ ∷ (B)容器中各部分温度相等,这△状态一定为平衡态; (C)容器中各部分压强相等,且各部分密度也相同,这一状态△定为平衡态。 i巍 藕 瑙 菝 窒 疋 衾 的分子数nェ =翌 匕竺苎E~纬2Lj 二、计算题: 冫 ∷ △ ∶ 1.图 中叭°间曲线是 lO0萜晶 氢气的等温绫,其 中压强 pl〓 4× 10:” ,九 ∷〓⒛ ×105Pa, 在 :畏;霭嬲}潜蜃:· ∵;∵势涔⒉=加f姆r∷ ∷ (2)氢气在b点和d点两状态的温度Tb和 Td讠 ·∶ 铭 T|F砷 P” 扩冉⒎κ TJ· 牦△9-`¨·33冫 κ 彳 ·'1|‘ I·
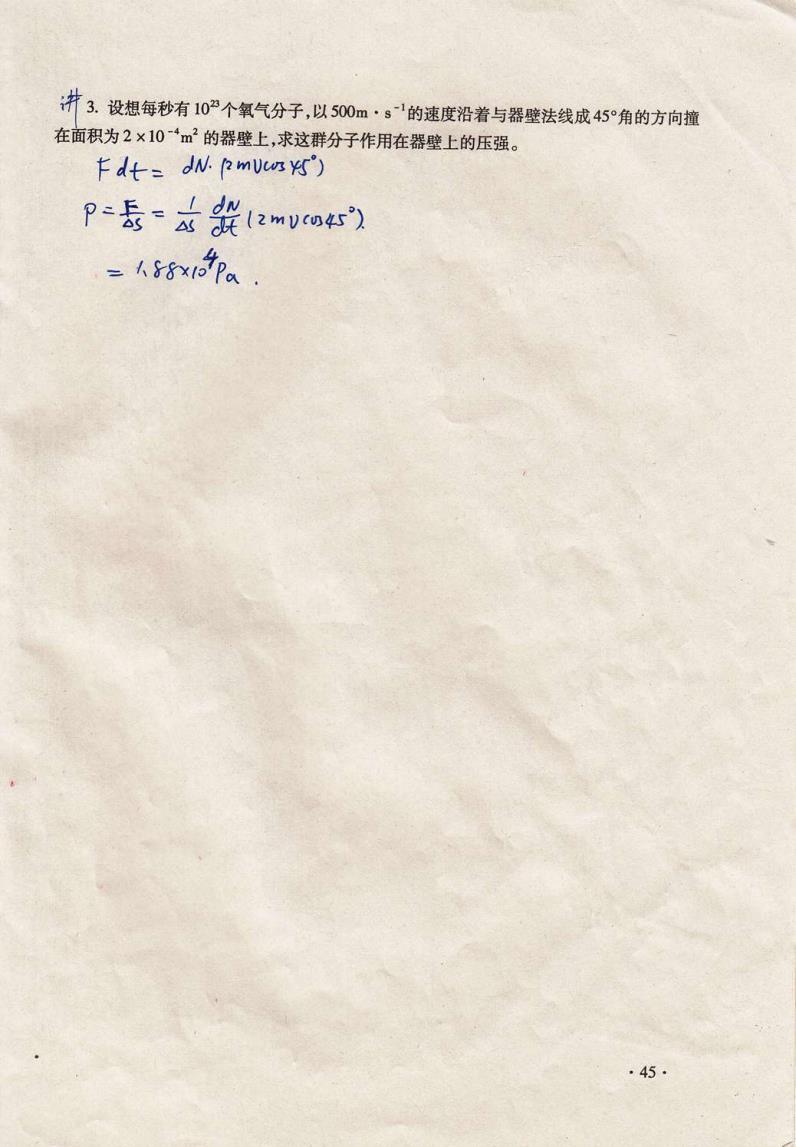
汁3.设想每秒有102个氧气分子,以500m·。'的速度沿着与器壁法线成45°角的方向撞 在面积为2×10-4m2的器壁上,求这群分子作用在器壁上的压强。 Fdt=dN.2mucosys) p=表太2mvo =人8xb印。. ·45-
△卜1Ⅰ 汇鸢岩篥量呈鹜戛矗扌肀 ∷ ∷|∷ ∷ ∶ 法罕|o:∴ 冖中|卩虍 i ∶∷∷∷∷∷ ∷ 1∶ |∴ ∷∷∷ Ⅱ∷∷ ∷∷∶ ,~I∷ ∷∷ ∷∷~ ∷∷∷∷∷ ∷∴|∷ ∷∷∷. ·45·

率的001干大率去其安,率数始元众某滤账为。(8) 世平的干食的内同 (二)麦克斯韦速率分布律术户某 一、选择题与填空题:币w) 1.速率分布函数()的物理意义是瓦速享附近¥位泳华匹门中的例教总妇热刷比字 2.说明下列各式的物理意义 (1)f(v)d速座左0vrdb正问内形好超总乡d都7恐此幸。 (2)Nf(v)dw速率左)24d)3酪分3数 (3)厂(o)dw在,心闪内恐'd整名兰好整的比率 (4)N()dw这车旅),≈y,词的d数 (5)f(v)dw年均速率 项,0阅 (6)。()dw淳车左0~之问0数5名3数的比球 处0=x 3.下列对最可几速率v,的表述中,正确的是: D (A)v,是气体分子可能具有的最大速率; (B),>u>√;$ 于公摩麻干食图 (C)速率分布函数f(v)取极大值时所对应的速率就是v,。 率板讯可晁 (D)在单位速率区间,分子速率处于心,附近的几率最大。 4.当气体的温度T升高时,麦克斯韦速率分布曲线的变化为: CD. (A)曲线的面积增大,最可几速率增大; (B)曲线的面积增大,最可几速率减小; (C)曲线的面积不变,最可几速率增大; 00 (D)曲线的面积不变,曲线的最高点降低。 5.图示为氧气的速率分布曲线,在此坐标中,试定性地作出氢气和二氧化碳在相同温 度下的速率分布曲线。 f(v) U 常由( 6.用总分子数N,气体分子分布函数()表示下列各量: (A)速率大于100m/s的分子数= ·35
(二 )麦兑斯韦速率分布律 一、选择题与填空题 : 3.下列对最可几速率 vP的表述中,正确的是: (A)%是气体分子可能具有的最大速率; (B\’ 石’属 ∷ ∷ ∷ ∶ (C)速率兮布函数“u,取极大值时所对应的速率耕是。p° (D)在单位速率区间,分子速率处于1p附近的几率最大。 4.当气体的温度T升高时,麦克斯韦速率分布曲线的变化为: (A)曲 线的面积增大,最可几速率增大; (B)曲 线的面积增大,最 可几速率减小; ∷ (C)曲 线的面积不变,最可几速率增大Ⅱ ∷ (D)曲 线的面积不变,曲 线的最高点路低。 5.图示为氧气的速率分布曲线,在此坐标叫,试定性地作出氢气和 =氧化碳在相同温 度下的速率分布曲线。 1 6.用总分子数‘N,气体分子分布函数“v) 示下列各量 : 2.说 ⒈解钸瞰 Kω nga螅婊五嵫迎丝幽幽缈喇鲫纫铆 确啐 明下列各式的物理意义: (4)NJ(∶ 《v)d。 ¢D (C、「)) (A)速率大于100Ⅱ/o的分子数= J

(国)多欢观察菜分子伦建率,发现其连率大于10a心的几车)dD 7.设某种气体的分子速率分布函数为(V),则速率在V一V2区间内的分子的平均 速率为 [vf(v)dv :熟空效盛就数, (A)vf(v)dv (B)f f(w)do(C) f(v)dv 1设两流代率纸 8.根据波耳兹曼分布律,温度T恒定时,处于一定速度区间和坐标区间的分子数与因 子 e-2kT 成正比,总能量E愈高的状态,分子占有该状态的 几率就 超小 因此,从统计观点看,分子总是优先占据 添邻量 状态的。 9在重力场中气体(分子质量为)温度T恒定,率就静直向上,2=0处的分子数密 度为no,则任一高度z处的分子数密度为n= n。e 若z=0处的压强为P,并测得高度z处的压强为P,则z与P的关系为2=一上CL卫 P。 二、计算题: 幸教大风的言具的世下种县u( 1.图为氢分子和氧分子在相同温度下的麦克斯韦速率分布曲线,求氢分子与氧分子的 最可几速率。 (3 o) VpHi= 041m=f网 含(q 京达,抽海氏子刻出的科产当 H ,大率讯四果,大用面的埃曲(A :小以素页量,大超商的曲年 670的01000 (m/s) 克密应理,变下用通的动( 调高量的发面,变不用面的所册( ·酯同2.假定N个粒子的速率分布函数为,中坐,曲动代率康的户岸式示 u,>v>0 是出公率数的圆 f(v)= o u>% (1)作出速率分布曲线; (2)由6求常数c。 (3)求粒子的平均速率。 (3)万=V 量使不示续()碳函市公正代产M黄子金总民ò 由比=装干啦em00干大率爽(A司 .36·
(B)多 次观察某分子的速率,发现其速率大于 10O〃s的凡绦犭JL圭丝暨上辶__丁 ⒎设某种气体的分子速率分布函数为-【V),则速率在Vl—ˉⅤ2区 间内的分子的平均 速率为 ∷ (台⊙ "店 灬PⅡ 子 8.根揖终耳萃 帚鹦 温擘T∴叵衣时,咎 于△衣淬擘珲间和坐标区间的分子数与因 ∷∴成正比,总能量卩愈高的状态,分子占有该状态的 几率就 ω `j? ,因此 ,从统计观点看,分子总是优先占据 %)v)Q v≥ % ∷ 称 锑 泔 状态的。 若 z=0处的压强为p。 ,并测得高度 平处的压强为 p,则 z与 p的关系为z〓 ^筚 h上 妫10瘛哙黯窍锸卢蛋 T℃早∷f猡 苴吐冖煳衍擗 二、计算题: 最可h逻窦帚 分子和 帚↑T≡T罕 I骂雩罚弓雩 尹 率分 卩 曲线,求氢分子与氧分子的 j早吾「许u例rF9彡 四 o 【ooo ″(`饣 /J) 2.假定 N个粒子的速率分布函数为 ⑴十甲 求粒子的 Ⅰ 均速率。 f-v)〓 {∶ tz7'辶 =诂、 tB,5=七V。 (1)作 出速率分布曲线; (2)由 uO求常数c。 V) C
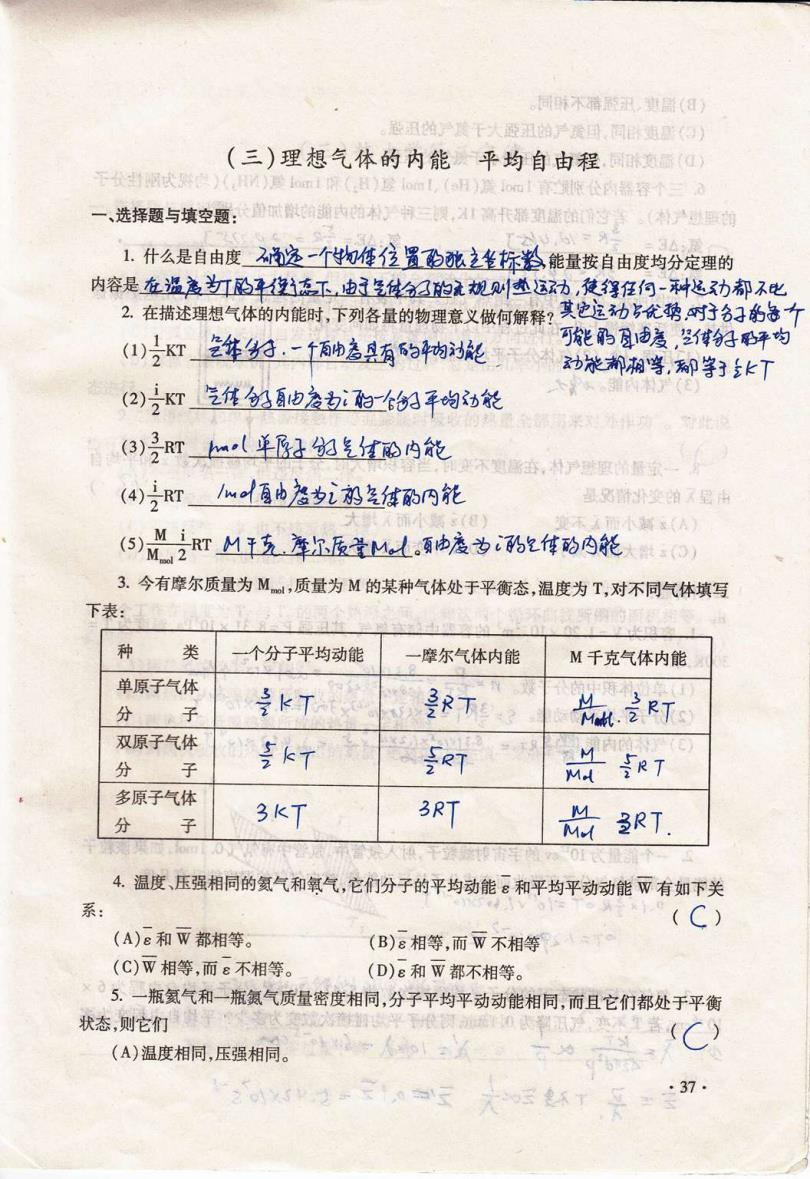
同味不猫讯,真高(日 卷温的户度干大登丑的产资过,间爽(传 (三)理想气体的内能平均自由程( 下量出状 H)金6m【,(H微om筑收企内器容个三2 一、选择题与填空题:自赋逾内的本中三视,高代瑞功盖的过学。(料划前 1.什么是自由度必个物修位置的弛之多标卷能量按自由度均分定理的 内容是在温高虹的平位志工由子色跑流规叫速运动,使得任何-科也动都不化 2在描述理想气体的内能时,下列各量的物理意义做何解释?其之运动优鸦网子台幻的各个 (1)片KT年纷.-个确嘉且有6的枘动能 可能弱月度,好卧评均 动米都湘学,即学子上T (2)KT汽体的他含阳的平的动能 (3)2rh(华服好的红的内能 不奥岳本,村户区的据金 (4)T叫厦地超的生体的内花 6骄姿的是由 (A (5说rM五泽沉质M酒凌为弱2付的内能 性0) 3.今有摩尔质量为M,质量为M的某种气体处于平衡态,温度为T,对不同气体填写 下表: 种 类 一个分子平均动能 摩尔气体内能 M千克气体内能 单原子气体 分子 kT 是RTE Mat.2RTs 双原子气体 分 子 多7 iRT M RT M 多原子气体 分 M 子 3KT 3RT 3RT 4.温度、压强相同的氨气和氧气,它们分子的平均动能ε和平均平动动能W有如下关 系 (C) (A)e和W都相等。 (B)ε相等,而W不相等可 (C)W相等,而e不相等。 (D)e和W都不相等。 5.一瓶氨气和一瓶氮气质量密度相同,分子平均平动动能相同,而且它们都处于平衡 状态,则它们 'C) (A)温度相同,压强相同。 之03p2一0
(三 )理 想气体的内能 平均 自由程 一、选择题与填空题: 1.什么是自由度 状态,则它们 ; (A)温度相同,压强相同。 能量按 自由度均分定理的 呷 艴 搀 刿 醉 纬 到 毕 缍 血 柳 丨伞运 2.在描述理想气体的内能时,下列各晕的物理意义做何解释?'簪 簪 孵 掣 黪 絮 弘 “跨胛芷 丝 争 △ 皿 勤 黾阝b伸v趁 : ∷畿 扬动馅 '哆 亻窜铉3鲆昀 南枇辫栩唔,,d9害 :乡 ″T ⑵ =KT Ξ饵铙 历汐鬼冫 亚士铂 徊 叱筏 ⑶:盯 龚 旦 勇 盔 堑 钍l±-o lb能 (4)去RT 柄丬甬南兔步氵鹉暨留酗冂徙 ⑶ 遘彦 RT迎吁么鸟扯血勋匹生。姒漉 VJ钙匕馆铅0筢 3.今有摩尔质量为 Mul。 l,质量为 M的某种气体处于平衡态,温度为 T,对不同气体填写 下表: 种 类 一个分子平均动能 一摩尔气体内能 M千克气体内能 单原子气体 分 子 害lc T 譬RT ‰。喾∷叮 双原子气体 分 子 享k下 畀 i 而渭|弯k丁 多原子气体 分 子 3kT 3尺T 黹 量RT。 4.温度、压强相同的氦气和氧气 ,它们分子的平均动能 ;栩平均平动动能 W有如下关 系: (A)ε 和 W都相等。 (C)W相 等,而 ε不相等。 (C) 5.一瓶氦气和 一 瓶氮气质量密度相 同,分子平均平动动能相 同:商且它们都处 于平衡 (B)ε 相等,而 W不相等 (D)ε 和W都不相等。 (C) ·37·

(B)温度、压强都不相同。 (C)温度相同,但氦气的压强大于氮气的压强。 (D)温度相同,但氦气的压强小于氮气的压强。 6.三个容器内分别贮有1mol氨(He)、lmol氢(H2)和1mol氨(NH,)(均视为刚性分子 的理想气体)。若它们的温度都升高1K,则三种气体的内能的增加值分别为: 氦:AE= R=84J 氢:4E=2R-22,25于 氨:AE=3R2丝.93了 自入 为不依什 7. 如图所示,在大气中有一绝热气缸。其中装有一定量的理想气体,然后用电炉徐徐 供热。使活塞缓慢上升,在此过程中以下物理量将如何变化? (1)压强;度(2)气体分子平均动能:场大 (3)气体内能。大 徐徐加热,盖板始终受力平衡,因此内压=外压(即大气压) 准静态等压过程 8.一定量的理想气体,在温度不变时,当容积增大时,分子的平均碰撞次数z和平均自 由程入的变化情况是 3) (A)z减小而X不变 (B)z减小而入增大 (C)2增大而入减小(D)五不变而入增大单式4T( 二、计算题: 不无T西露谢平件的利户某的比道巴以快贵面不信 1.容积为V=1.20×10-2m3的容器中储有氧气,其压强P=8.31×10Pa,温度为T= 300K,求内克 83之*aolx106/4e2 (1)单位体积中的分子数。n*长行38.3? (2)分子平均平动动能。=KTx130以w以x3N二6,4×16J (3)气体的内能聪整RT。312x0芝 ≤).4331o灯 2。一个能量为102ev的宇宙射线粒子,射入氖管中,氖管中有氖气0.1mol,如果该粒子 的能量全部被氖气分子所吸收而变成分子热运动能量,试向氖气的温度能升高几度 0、1×是RoT=1.1.62x。9T oT-2x1心忆 验球话床aA 南3,氮气在标准状态下的分子平均碰撞次数为5.42×10。,分子平均自由程为6× 10-6cm,若T不变,气压降为0.1atm,则分子平均碰撞次数变为多少?平均自由程变为多 T 少?入节 入-1o¥入=6 X Lo-CM 登丑,闻卧物(k ·38z=头T待2大 ze0,1z=52x1o7s
(B)温度、压强都不相同: (C)温度相同,但氦气的压强大于氮气的压强。 (D)温度相同,但氦气0g压强小于氮气的压强。 6.三个容器内分别贮有 1m。l氦 (He)、 1m。l氢 (H2)和 1mol氨 (NH3× 均视为刚性分子 叩理蛋嘿 。∷璧甥篙掣 高κ,℃皙T瑾茎l昱鲨 氨:ΔE〓 ;RG,″J生 7.如图所示∷,在大气中有一绝热气缸:其中装有⊥定量的理想气体,然后用电炉徐徐 供热。使活塞缓慢上升,在此过程中以下物理量将如何变化? (1)压强;冫哇 (?)气体分子平均动能;磁 fx (3)气 体内能P〃钎 ` 8.-定量的理想气体,在温度不变时,当容积增大时,分子的平均碰撞次数 Ξ和平均自 由程X的变化情况是 (A)Ξ 减小而 `不 变 (B)Ξ 减小而X增大 (C)Ξ 增大而X减小 (D)Ξ 不变而X增大 B) 二、计算题: ∷ 1.容积为 Ⅴ=1.⒛ x10ˉ 2m3.的 容器中储有氧气,其压强 P〓 8.31× 10FPa,温 度为 T= 3叩 【丨:;圭莅体积中的分子数。r∶ 亻1oJ裴 扌E蚕Ⅰ£ a氵 ∷∶丨∶∶γ (2)分子平均平动动能。£ t| =毛f奸 t讠吲 (3)焉已体的”年照孕芒R1 《 是登罡釜妻莛|竺 y适 (a~吖 :只 `。 ψJ 2.一个能量为1d2ev的宇宙射线粒子,射人氖管中,氖管中有氖气0。 1“o1,如 果该粒子 的产帚气骂挲晷矛£霞玎娶贤巩气蜜罕雳窜 运动胄吕量,F向 氖气的温庳能尹高几度 ^T=`、 冫阝 冖广 冫 丨‘ ∷ 3.氮气在标准状态下的分子平均碰撞次数为 5。 0z× 10:s^1,分 子平均 自由程为 6× ‘λ g笮 骂 繁窍窍声 少?平均自由程孪为多 冫、fΞ ≈占∴ψˇro⒎s。 r, ` //

沙 第九章 热力学 (一)热一律、热一律对理想气体在等值过程中的应用 一、选择题与填空题: 1.内能是好能无步能加 。 热量 是电好慢嘉径径的乃力的驰生 —。内能和热量这二个物理量的主 要区别是内花是状连是,尘量是过张多 2.在等容过程中,系统内能的变化为△E1,在等压过程中,系统内能的变化为△E2,则 (B) M C.AT,AE=M (A)AE= M C.AT M C.AT,AE=M (B)AE= M C.AT (Ca=总c,a.a,-总c,a 3.图中AB为等压过程,BC是绝热过程,CD是等容过程,DA是等温过程,一定量的气 体作ABCDA的循环过程,试以正、负或O填入下表: 过程 △V △T AP A AE Q AB 正 正 0 正 正 正 BC 正 免 免 正 负 CD 0 正 正 正 DA 丑贞 D 员 4.一定量的理想气体在以下各过程中所吸收的热量为Q,对外作功为A,内能的增量为 △E,将Q,A、△E的计算公式填人下表: ·38·
第九章 热力学 ∶ ∷ ∷∷∷. ∷∷ j ⅡⅡ ∷∷∷Ⅱ | ∷ ∷∷ Ⅱ∵ ∷ t ∷∷ ∷ ∷∷∷∶ ∷!∷ ∷ ∴,∷ 、∷ ∶ ∶∷∷ ∷ ∷∶∷ ( ∷ = ∶f (ˉ )热 ∵律∷=热∵丁律对理想气体在等值过程中妁应用 ∷ ∷∶∵ !∷ ∷ ∴ ∴ ∶ ∷∷∷ -、选择题与填空题: 1.内 能是 锯 虢 品磅牝J卜 °热量 是~砷3Ⅲ砑猊丑旦凶鳌日刍涩卫鱼豆土m渔卸望笠~工°内能和热量这二个物理量的主 要区别是 内筢邑 状拼 。僻 扭苞诩H∴ 。 ?.在等容过程申,不绋巾熊的孪化为岬1,在等压讨程中?不绅”熊叩孪华汐邓Ⅱ贝刂 ∷ ∷∷ ∷ ∷∷∷∴∷∷ ∷∶∶∷∷(Ⅱ-巳9 CA)Δ△亠+芍∵ 咖 ,Δ黾=却 p兮T (ω Δ△〓 毒 C。 ΔT,ΔⅠ坛=毒CΨ WT (0Δ宝:=毒cp“ ’胡2|毒Cp呷 3-图 中AB为等压过程,0C是绝热过程,qo是等容过稃,p^是等温过程,∵窄量的气 体作ABCpA的循环过程,试 以正、负或0填入下表: ∷ ∷ 4.一定量的理想气体在以下各过程中所吸收的热量为Q,对外作功为 A,内 能的增量为 ΔE,将 Q,A、 AE的计算公式填人下表: 。3∷ 8· P 过 程 ΔV AT累 AP A AE Q AB 正 工 0 正 正 正 BC 正 泛 场 千 τ 灸 9亠 CD D 正 正 0 正 证一 DA 边 o 裳应 太 D 突

过程 过程方程 △E A Q 等容 V=C T(P;PIV 0 itp:-PV 等压 P=c tPlVz-V) P(D:-Vi) P-) 等温 T=c D vTln告 UnTl 绝 热 Q=o w.-PV) CRV,-PVz) 5.质量为1kg的氧气,其温度由300K升到350K,问内能改变了多少?其升温是在下 列三种不同情况下发生的: (1)等容过程:△E= 3246o93 (2)等压过程:AE=九4~.9丁 (3)绝热过程:4E=3246m,9了 6.一定量理想气体,从A状态(2P1,V)经历如图所示的直线过程变到B状态(P1, 2V,),则AB过程中系统作功A= P业4 ;内能改变 △E= ·7.一定量的气体从体积V1膨胀到V2,可经历以下几个过程,如图所示,从A→B等压 过程,从A→C等温过程,从A→D绝热过程。问: (1)经历哪一过程作功较少 AD (2)经历哪一过程内能增加 AB (3)经历哪一过程内能减少 A-D (4)经历哪一过程吸热较多 42B 39·
过 程 过程方程 ΔE A Q′ 等 容 ¢-C¨ 已∷ 氵 ∷ ’ / · 丶△ 一⒉ l’ 丶 /〓 ' 〓 卩 z 一 ∷~∷^卩 丶● 一z 等 压 P=c 考Pt〃冫't/.丿 P(冫 :一 vr丿 :° ·PC^亠Ⅱ丿 等 温 T二 G 0 、κT饫 年 '冖 %年 绝 热 Qo夕 芳叱队ˉ卩‘/D t _ D" ` 、D一 乙 -h/P, 口 ∷∮庶堇为ii∶ 的刍点,直 值查占j沆k卉勤3s。 讧 ∴亩莴能蔹圭÷ ∶ 多j0∶直卉疽嘉在+ 列三种不同情况下发生的: 、 (1)等容过程:AE〓 夕坪洳 · `J。 ∷ ∷ ∷∷∷ . ∴ = (2)等压过程:Δ宜|∷ 如砷加,`J (3)绝热过程:ΔE〓 召乙屮幻、 6.一定量理想气体,从 A状态〈2P1,Ⅴ `了 】)经历如图所示的直线过程变到 B状态(P1, 2V1),则 AB过程中系统作功 A=t÷__皂⒓」刍._⊥_______⊥ ⊥;内 能改孪 ΔE〓 F, 。 ⒈ ': 2': U /∶ /:∷ / ·7。 一定量的气体从体积Ⅴ1膨脓到 V∶ ,可銮历:以卞几个过薤,如 图所示-从 A→B等压 过程,从 A→C等温过程,从 A→D绝热过程。问: ∷ (1)绎历哪一过程作功较少 肖ˉ》D ∷ (2)经历哪一过程内能增加 4-9B (3)经历哪一过程内能减少 (4)经历哪一过程吸热较多 ^-,9 丨。 冉田s ·39·

二、计算题: 1.一定量的某种理想气体在等压过程中对外作功为200J,若此种气体为单原子分子气 体,则该过程中要吸热Q为多少?,若此种气体为双原子分子气体,则需吸热Q2为多少? Q=变A Q,=号20=0了 Q2=2×207mJ 2.质量为M,温度为T的理想气体(摩尔质量为M)在等容下冷却,使压强减小到原 来的二,然后在等压下膨胀,气体末态温度等于初态的温度,试计算这一过程气体所作的功? PiVI-PA R=HP VEnvi 丹=P,(-M=元P,(nW,-4) BV =以R-只aRT 3.1mol氢气,压强为1atm,温度为20℃时体积为V(1)先保持体积不变,加热升温至 80℃,然后等温膨胀到体积为2V。;(2)先等温膨胀到体积为2V。,然后等容加热到80℃,试 分别计算两种过程中气体吸收的热量、增加的内能和所作的功,并在同一P-V图中作出表 示二过程的曲线。 ,(1A=A灯Rz(传=131×33lm2=22.3订 △E=R(TT,)=三×1×81×6心=245了 Q=+8E=3271,8了 (2)月=AT=pRT,ln条=1x8x23(n2=1627J sEiveCn-T)-n65J R=A+E=213失2 40
舻 二、计算题:∷ ∷ ∴ ∷ ∷∷ ∷ 1,一定量的某种理想气体在等压过程屮对外作力为⒛OJ,若 此种氖体为单厚子分子每 体,则该过程中要∷吸热 Q1为多少?,若此种气泳为双庶宁芬子气体,则需畈热 Q2为 多少?ˉ Q· 乎^∷ ∷ ∷ ∵∷ Ⅱ ∷ ∴∷ 夕i=Ξ告灿冖=少¨J Q⒎ :艹 亻z” 氵刂 :∷ 2.质量为 M,温度为 T的理想气体(摩尔质量为 Mm。l)在等容下冷却,使压强减小到原 来的÷L,然后在等压下膨胀,气体末态温度等于初态的温度,试计算这一过程气体所作的功? n= Ⅱ ∷。 ∷ ∷△∷ ∷ ∷ b. ∷∶ ∷ ·f ∷ P1丌△冖L汀 良△R浴访% 虍`巳 (h亠%氵:万 民("v’ =Ⅱ 9 ∶ ⒎艹 汛 =艹‰ 吖 ∵ 3.1mol氢气,压强为1aun,温度为⒛℃时体积为V。。(1)先保持体积不变,加热升温至 gO℃ ,然后等温膨胀到体积为2V“ ;(2)先等温膨胀到体积为2%,然后等容加热到sO℃ ,试 分别计算两种过程中气体吸收的热量、增加的内能和所作的功,并在同一P-Ⅴ 图∷中作出表 ‘∴l黠 ±释 iii阱 =,∶ ⒏:`i引刂丨⒒·二⒉ ∶|廴 乏1 ∷F ^E-=劣 ’Rc⒎Ⅱ,9F菩 不 `∷ 汪Ji× 灿 =,W】r5, ∷ Q-府 艹 ^多 △‘2〃t圮 t乙 'PO奎 讲 T亠 ^∵ Rt|l"自 方 F`亻 ε||7犭 冫 `3(η ?=/亻'⒎`J ∷ 犭‘俏`'c⒎ △)ˉ Ⅱv·“△ ¨ ∷ ∷ R彡 舛 +疹 E一 二 2`3饮 zJ Ⅱ ∵ ·40·
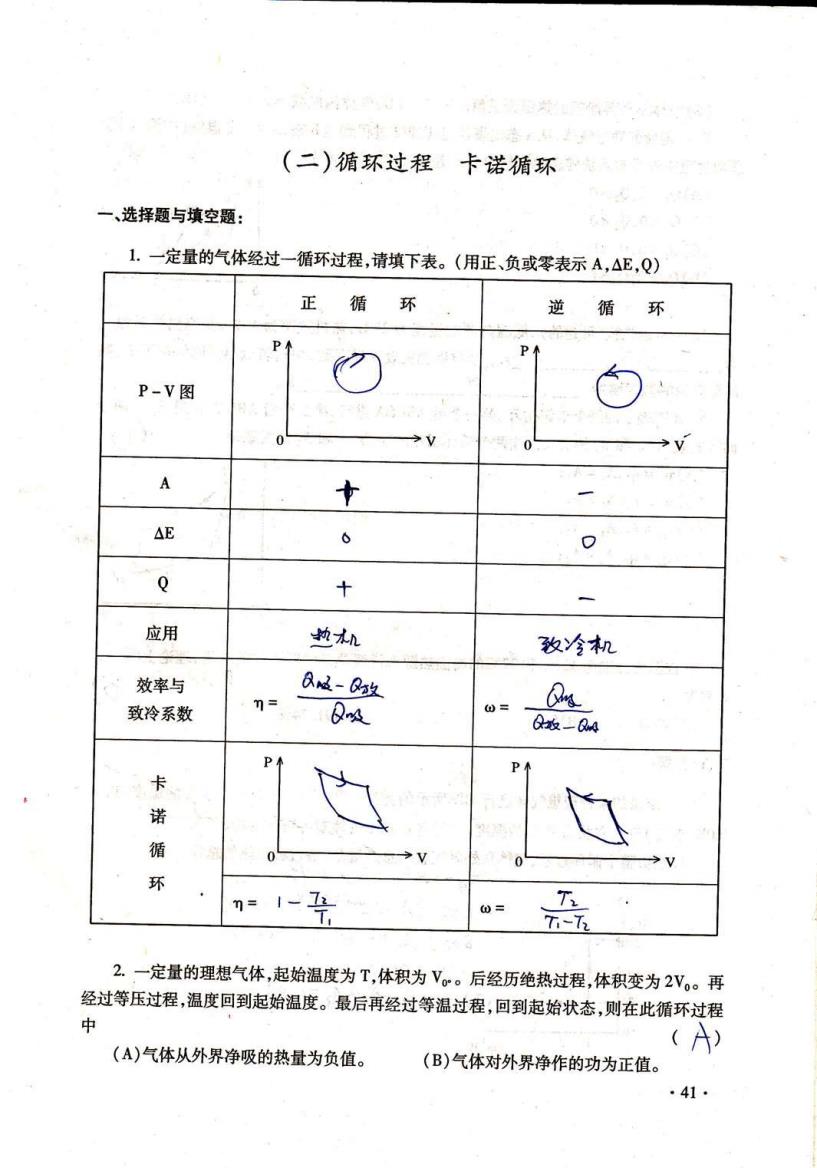
(二)循环过程卡诺循环 一、选择题与填空题: 1.一定量的气体经过一循环过程,请填下表。(用正、负或零表示A,△E,Q) 正 循 环 逆循 环 P-V图 E A 古 AE 6 Q + 应用 地木n 孜冷机 效率与 and-k d 致冷系数 = 0= Q放-Qa P P个 卡 诺 循 V 0 环 n=-名 0= 、 T-7 2.一定量的理想气体,起始温度为T,体积为V。。后经历绝热过程,体积变为2V。再 经过等压过程,温度回到起始温度。最后再经过等温过程,回到起始状态,则在此循环过程 必 (A)气体从外界净吸的热量为负值。 (A) (B)气体对外界净作的功为正值。 ·41…
(二 )循环过程 卡诺循环 ˉ、选择题与填空题: I.△定量的气体经过一循环过程,请填下表。(用正、负或零表示 ^,Δ E,Q) 2.△定量的理想气体,起始温度为T,体积为吒。。后经历绝热过程:体积变为2%。 再 经过等压过程,温度回到起始温度。∷最后苒经过等温赶程,回 到起始状态,贝刂在此循环过程 中 (A)气体从夕卜界净吸的热量为负值。 (B)气泳菇夕卜夷净讵品功克⊥值。 ( ∧ ) ·4I· 正 循 环 逆 循 环 孜嗨+t 效率与 致冷系数 η〓恤 ρ冂岱辶 逸咖 卡 诺 循 环 η=Ⅱ 夸 ω〓 `TL