
第十五章 量子物理基础 光电效应(一) 二、填空、选择题: 1.关于光电效应有下列几种说法,正确的说法是: (A)任何波长的可见光照射到任何金属表面都能产生光电效应; (B)对同一金属如有光电子产生,则入射光的频率不同,光电子的初动能不同; (C)对同一金属由于人射光的波长不同,单位时间内产生的光电子的数目不同; (D)对同一金属如有光电子产生,若人射光频率不变而强度增加一倍,则饱和光电流也 增加一倍。 2.已知金属钾的逸出功为2.0ev,如用波长为3.6×10-7m的光照射在钾上,则光电效 应的遏止电压的绝对值1m,1=_人5V 一。从钾表面发射出的电子的最大速 度V= 714%10ws 3.用频率为v的单色光照射某种金属时,逸出光电子的最大初动能为E,若改用频率 为2v的单色光照射此种金属时,则逸出光电子的最大动能为: (D (A)2E (B)2hv-Ex (C)hv-Ex (D)hv+E 4.某单色光照射到一金属表面产生光电效应,此金属逸出电势为U。,则此单色光的波 长必须满足: (AA荒 (A) (B)λ he eUo A-euo (GCa兴 (D)≥C eUo hy-At3ww>A 5.在均匀磁场官内放置一极薄的金属片,其红限波长为入,今用单色光照射,有电子 逸出,逸出电子(质量m,电量绝对值©)在垂直磁场的平面内作半径为R的圆周运动,那么 此照射光子的能量是: ⑧ (光 (B)hC(eRB)2 2m Ee=hy-A=h7-4 (c光盟 (D)C +2eRB =wWp路y:竖 6.以一定频率的单色光照射在某种金属上测出其光电流的曲线如图中实线所示,然后 在光强度不变的条件下增大照射光的题率。测出其光电流的曲线如图中虚线所示,满足题 欢八个 w 知热↓ =+ g
第十五章.量子物理基础 光电效应(一 ) . 二、填空、选择题: 1.关于光电效应有下列几种说法,正确的说法是: ∷馏2° (A)任何波长的可见光照射到任何金属表面都能产生光电效应; (B)对同工金属如有光电子产生:贝刂人射光的频率不同:光 电子的初动能不同; ∷ (C)对同一金属由于人射光的波长不同,单位时恂内产生的光电子的数目不同; ∵∴∷ (D)对同厂金属如有光电子产生,若人射光频率不变而强度增加△倍,则 饱和光电流也 增加ˉ倍: ′ 2.已 知金属钾的逸出功为2。 0山 ,如用波长汐3.6× 1。 ˉ7m的光照射在钾上 ∷ ,贝刂光电效 应的遏止电压的绝对值丨u巴 丨=___r.竹 / 。从钾表面发射出的电子的最大速 度 V1mx- 3.用频率为v的单色光照射某种金属时,逸 出光电子的最大初动能为Ek,若改用频率 为 加 的单色光照射此种金属时,则 逸出光电子的最大动能为: (J.∶)冫) ′∶CA)2Ek (B)2hvˉ Ek (c)hvˉ Ek (D)hv+Ek 4.某单色光照射到一金扁表面产生光电效应,此 金属逸出电势为 U。 ,贝 刂此单色光的波 长必须满足: ˉ ⑴λ≤螽∷ ¨ (”≥螽 ⑹卜贽 ⑼λ≥辔~ 5.在均匀磁场 氵内放置工极薄的金属片,其 纟 黥 瞿 辘 鼽 :?电 勤 γ 值 e,a垂直 箩孑蛋 严面内f节径为 R胴 胧 T钅 ∷ (A)等 (:冫 等+午罴亻 E0亍 b′ ^A画杭P一 名膏 ∷ (9等 +訾 ∷ 。 ⑼等+2eⅢ 0以一定频率的羊色光照射在某种金属上测出
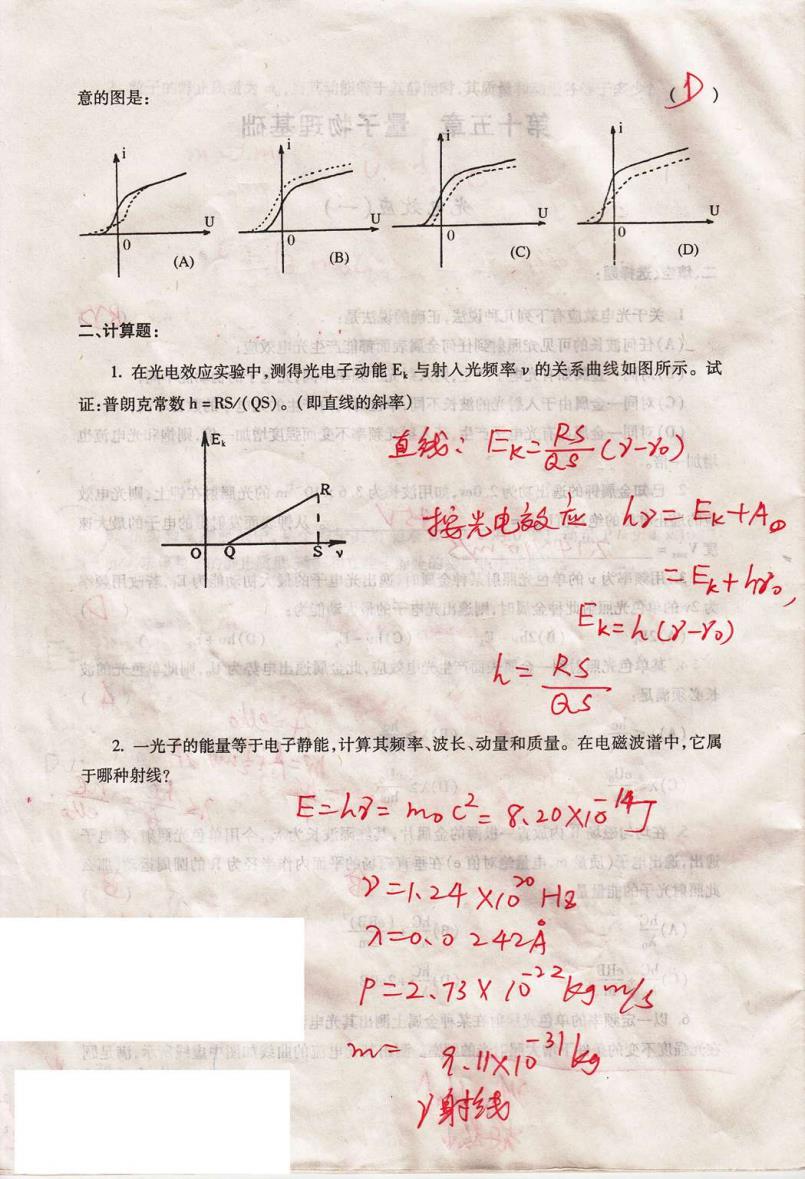
意的图是: 杯基野干昌 (D) 二计算题: 海面对可合血峡兴干关 1.在光电效应实验中,测得光电子动能E,与射入光频率v的关系曲线如图所示。试 证:普朗克常数h=RS/(QS)。(即直线的斜率)不地人千由 所中疗圆 E 道线k器y-为 必冲兴调,士 R 南大任申 摇光电数应yEk+A。 0 用弦江 -Ekthio Ex=hl-Y) 如的光座,的装申出欧通试,血必兴 儿=卫S单 as 淑新厌尊列 2.一光子的能量等于电子静能,计算其频率、波长、动量和质量。在电磁波谱中,它属 于哪种射线? E-A7=m2g20X。4 出新出烟 )人24X10°H2 前气物码线 7=0、0242A P=273Y1⊙' 园,虫中装业的远生仁 7x10到 Y射线
意的图是 : ρ ) 二1计算题: . 、∷ ∷ ¨ I ∶∷∷ ∶ ∷∷ ∶∷Ⅱ∵ ∷∷ ∷i|∷ .∶ 1.在光电效应实验中,测得光电子动能E1与射人光频率9的关系曲线如图所示。试 证:普 朗克常数 ht尽γ(Qs)。 ∷(即直线的斜率) ∶ ∷ ∶ ∵ 崖乙勿δj 氏二∵笋△一y。9 磁娅廒扛∷芘’ · =k胡ρ Ⅱ i· 讠十丿oξ .∶ |丨 ∷.∶ ' ∷f庄 皮乙 `一 FD9 t=焦∷‘∴∶ “ ∷ 2.一光子的能量等于电子静能,计算其频率、波长、动量和质量。在电磁波谱中,它 属 于哪种射线?∷ F|^7|Ⅱ △∷卜Dx/T勹 ∷ ∶∶∶∵∶∷∴∶|Ⅱ ∵∶∷ '二 ∫`△午×/。 ∷Hg 9=>o、 o△翎 ∵ `||∶ 7‘ Y/。 ^)勹屯 力:″× `孑 -- :!=该乡 /豸1彡钧 =∶ ~ˉ _ˉ __ _~ —·∴=舔 ∶∶f舷癞 -/×

康普顿效应(二) 一、填空、选择题: 1.某一波长为入的x光经物质散射后,其散射光中包含波长 70 和波长 >2两种成份,其中:入>。的散射线成份称为康普顿散射。 2.康普顿散射中波长改变量最大时散射角φ=丁 此时Aλ= 044 可见光中波长最短是X=400m,则A0-【X10。 此结果表明用可见光作为入射 光线观察不到康普顿效应。 /6C 3.在康普顿散射中,如果设反冲电子的速度为光速的60%,则因散射使电子获得的能 量是其静止能量的Q2S倍。 4.用强度L,波长λ的x射线分别照射锂(Z=3)和铁Z=26),若在同一散射角下,测得 康普顿散射的x射线波长分别为入u和入(入u,入均大于入),它们对应的强度分别为lu和 1,则: (A)Au>AFe,Iu Ipe (D)λu<入a, Iu Ipe 二、计算题: 1.用入=0.lnm的光子做康普顿散射实验 (1)散射角中=90时的康普顿散射波长等于多少? (2)分配给反冲电子的动能等于多少? )7-7%+=01t00o24=0、lD2+ =人024A C Ek-e-六)=466x0J ≥191wW
康普顿效应(二 ) -、 填空、选择题: ⒈ 某一波长为 λ。的 x光经物质散射后,其散射光中包含波长 ∷⒎。 和波长 ⒎ J J〓 Ⅺ D 〓 ⒋ `’ rD `丿 J一 T ^ 喘 ^>λ 。 南种盛¢⒎枣中 λ >⒎0 的散射绋成份称为康普顿散射。 。 9康普顿散射中菠苌鼓变量最大时散射角 0二Ⅱ`△「 ∴∷∷,此时加F御 可克光中波苌最短是 λ三Ⅱ ηm,则年 △ 《rD^J。 此结果表明用可见光作为 ^射 光线观蔡木slj康 普顿效应。 3.在康普顿散射中,如果犭∶空沛电子的速度嘉兔馐蚀%孔b,则 因散射使电子获得的能 量是其静止能量的 矽`)ζ 倍。 4.用强度 I,波 长∷ `的 I科线分别烬射锂(z〓 β)和钵 Ξ÷冗),若在同ˉ散射角下,测得 康普顿散射的攵射线波长分别为 λu和 λFe(λ Ⅱ,λ诂均大于 λ),它们对应的强度分别为 ILl和 IFe,贝刂: ∷ Ⅱ 乙 (A)λL1≥ λFe, IL1<IFe (B)λ L1亠 λFe。 IL1|IFe ∶ (C)λ L1〓 λ., ILl)IFe ∷ (D)λ L1(λFe, I∵∷I”∶∶ =o计箅题: ∷Ⅱ 1.用 λ。亍0· 1nm的 光子做康普顿散射实验 {∶ }繁繁垦羞亓彗 雩 于罕t 乙l,a亠 ,J+M二 o· 丨卞0§氵 夺△9、 J蚪 ~ ∷ =丿 、:∶ 0冫 +' ˉ C〓L-'冫 Fk亠 tG 冫△9`勘/ 、b纡 瓴幽‰ 一 =ˉ=ˉ= ˉ-— ·`— -———`ˉ-¨ — = - —△ △ ~ˉ ~~~ ~~~← 一一ˉ-ˉ -— ˉ-· ˉ--———-ˉ^

2.一光子与自由电子碰撞,电子可能获得的最大能量为60kv,求入射光子的波长和能 量。 0=T △入=0048A 出热+ khcC分-石a) 料:空就 7。=0∂786A 联武的单 的斗干超平减全手,主小效 不日 E=158keWe153x元与 湖出 3.已知x光光子能量为0.6Mv,在康普顿散射后波长改变了20%,求反冲电子获得 的能量和动量的大小。 , 刀=人27。 k=人eC元-入)2o1MeV=6xo P=E-母 C =人79X0kgm5 二七6+2
量 。 ⒉ 一光子与自曲电子碰撞,电 子可能获得的最大能量为ω夂ev,求人射光子的波长和能 叼:可 ∷∶厶 `亠 ?、 ° 4召 A %— ^汪 --寺 | ⒎Pt丬 0 i ∷D口 干 c9-· p∷ `ε 亻 ^.¨ ∷∶. E亠 ∷ `|扩 ∷如g/=∷亠:占 ζ×.'否 Ⅲ Ⅰ Ⅱ ∷ ∷ . ∶ · ∷ ∷ - ∷ |=∵ | ∷ i ∵ 3。 已知攴踮先字彘量为o.6Me△,,在康普镟嵌荮启菝苌蔹芟宁茄庞:汆庋济电竽蔌得 的能量和动量的大小。 a≡∴卜氵?:ˉ ∴ 钆|Ⅱ订|缄 勹 P: √·一 〓一 h ‘ 丿 G △女)∵ ⊥。1∫ 州c/土 `么 v厂鬯冫 亠z之 xF° 幻m/× 拓 姥 蚴 钌

氢光谱 玻尔氢原子理论(三) 一、填空、选择题: 1.当一质子俘获一个动能E,=13.6v的自由电子,组成一基态氢原子时,所发出的 单色光频率是 6.56x105 Hz 2.能量为15v的光子从处于基态的氢原子中打出一光电子,则该电子离开原子核时 的运动速度为 702 io mls 3.氢原子光谱的巴尔末系中波长最长的谱线用入表示,其次波长用入2表示,它们 的比值皖 27o=13乃,→利n:2的班 4一个氢原子处于主量子数n=3的状态,那么此氢原子 1:32 ‘4 (A)能够吸收一个红外光子; (B)能够发好不径外光子 (C)能够吸收也能够发射一个红外光子; (D)不能吸收也不能发射一个红外 光子。 二、计算题: 1.气体放电管中,用能量为12.2v的电子去轰击处于基态的氢原子,则基态氢原子 能跃迁到n等于几的能级,能发射的谱线的波长等于多长? -3 成2,) 71=1D28A 7=1218A 73÷6577A
氢光谱 玻 尔氢原子理论 亠1填空.选择题: ~ ∷ ∷ ∷ ∷ 1.当 一质子俘获一个动能 宝k〓 13。 仉v的 自由电子,组成工基态氢原子时,所发出的 单色光频率毫 ° 2.能量为 15山 nt光子从处手基态的氢原子中打出工光电子:则该电子离开原子核时 的运劫速度为 ∷7`02X/Dc0叼 忽 。 ∶ 3.氢原子光谱 中澳长最长的谱线用λ1表示,其次波长用λ2′ 表示,它们 彡刂汽|冫 ∷的徽 ⒋L木氢原子处车圭量子数 h=3的状态,那么此蠢原字 al1扌 '⒓ (夕 (A)能够吸收一个红外光子; 石%施晶鳄多卜光宁; (C)能够吸收也能够发射△个红外光子; (D〉 不熊吸咚也不熊发射△↑纡外 光子。 ∷ 二、计算题: ∴ 1.气体放电管中,用能量为1?.2ev的 电子去轰击处手基态的氢原子,则基态氢原子 能跃迁到h等于几的熊级,能∷发射∷的谱线的波长等于多长? ∷ ∷ ∶讧⒊⑼记毛1D 冖 `△ `D∷ 勤廴∴ ∩Δ←1`△丬⒏冯∷∶ n亠 =Ⅱ jL→|尻 : `咖 〓一 〓 ( ∷^ 助Ψ钠

2.氢原子光谱的巴耳末线系中,有一光谱线的波长为434nm,试求: (1)与这一谱线相应的光子能量为多少电子伏特? (2)该谱线是氢原子由能级E。跃迁到能级E,产生的,n和k各为多少? (3)最高能级为E,的大量氢原子,最多可以发射儿个谱线系、共几条谱线。请在氢 原子能线图中表示出来,并说明波长最短的是哪一条谱线。 c)E=458x109=2.86e/ 中中学电 n-)n-5,k-2 是 C)4什线系10条谱线 计 波长最短 n25之1s/ 3.氢原子激发态的平均寿命约为10s,假设氢原子处于激发态时,电子作圆轨道运 动,试求出处于量子数=5状态的电子在它跃迁到基态之前绕核转了多少圈。( m。=9.11×103kg,e=1.6×109C,的t6名 .h=663×I0JS,8o=8.85×102C2.N.m2痕04个中普 0.00了 e' 应王报年中润 ←千T0r3 议日泌补干量暗同 年E中@ mur=nh 8 W=号=Xo 网乐的1下所空中过海了的鱼=中下 斯的 可
2· 氢原子光谱的巴耳本线系中,有一光谱线申波长为Ⅱ4nm∶ 试求: (1∷ )与淳T谱线相应的光子熊晕为多∷少串子伏≈∷?∷ ∴∷ ∷Ⅱ∷ ∷ - (2)该谱线是氢原字由能皱 蜕映迕勤能级 Ek产生的,nffn k各为多莎Ⅱ .-3)最高能级为 E5的大量氢原子,最手可u察科九个谔线系、共几荼谱线。请在氢 原子能线图中表示出来,并说叨波长最媸的是哪ˉ条谱线: ∷∷∷ I ∷ Ⅱ=:+窍又 '矿 彳 '|土 吖山/ 印?∷ ”亍s||乜 |i G· )4饣线虿∷∷∷I扌橥∷∷名线 :葭磁桑艹直 η下 '㈦ 3.氢原子潋发态的平均寿命约为 10:s,彼诀氢凑手处于激发态时:黾 子依圆轨道逶 动,丬求出处于皇子数 n=5状态的龟宁在击跃迁到基态之前绕核转了多少圈。 ∷∷∷∷ me F⒐ 11*10flkg|e△ 1,-x】0=尸C,∷ ∷.∷ ∷∷∶∷∷∷∷∷-Ⅱ ∷∷∷ ∷ ∶∶0tf· f3犭 1ρ 「 p4J· s.乱 |β.卩,× IQ∴ : C?.∷ N∶ 。∷m?- ∷ ∷ 卜Ⅱ— .仉 ∷∶ ∷ rI o十∶亠 ∷∷ ∷ ∶/ Ⅱ ∴∷ =∷ ∷△ ∷∷ ∷ ∷ ∶ ∶∷ ∴ 〃呀0嘭∷∴T|∷弓盯 ∷讠二∷r∶ ∷丁 ∷∷ ⊥、|∷

微观粒子波粒二象性测不准关系(四)》 一、填空、选择题: -35 1.一质量为40×10-kg的子弹,以10005的速度飞行,它的德布罗意波长为人b6X0 一。所以子弹不显示 波生。上mW广e心 m是 2.一束带电粒子经206v电势差加速后,其德布罗意波长为0.Q02m,已知此带电粒子 的电量与电子电量值相等,则此粒子的质量为人67X1心 。 3.静止质量不为零的微观粒子作高速运动,这时粒子物质波的波长入与速度ⅴ有如下 关系: ( (A)λcV (B)AcY (D)xx√C2-V 4.α粒子在磁感应强度为B的均匀磁场中沿半径R的圆形轨道运动,则α粒子的德布 罗意波长是: (A)h/(2eRB) (B)h/(eRB) B.n 开) (C)1/(2eRBh) (D)1/(eRBh) 5.如图所示,一束动量为P的电子,通过缝宽 为a的狭缝,在距离狭缝为R处放置一荧光屏,屏 上衍射图样中央最大宽度d等于: D> (答 (® (D2 6.关于不确定关系△x△P,≥h(h=h/2π)有 以下几种理解: (1)粒子的动量不可能确定。 (2)粒子的坐标不可能确定。 (3)粒子的动量和坐标不可能同时确定。 (4)不确定关系不仅适用于电子和光子,也适 用于其它粒子。 其中正确的是: () (A)(1),(2) (B) (2),(4) (C)(3),(4) (D) (4),(1)
段观粒子波粒二象性 测不 准关系《四) ∵、==J虫惑△∵Ⅰ∷ ∵ -∷ ∵Ⅱ ∷ ˉ 飕 t。·0× ⒛执 0gf弹 ,以 1000m/s魄夙 行,衲鲫 脲 涨 为山 ‘砺 饣 彡L力凵L丝⊥_。 ′ ~。 圭而廴J山 丿讠耄鞋与浒杂 一 所以子弹不显宗 冫立 丿 r 2.一束带电粒子经2“v电势差加速后,其德布罗意波长 的电量与电子电量值相等,贝刂此粒子 ∷的质皇为 ∷ 火 ‘7讠 关系: (∷ ^)λ ∝V 3.静止质量不为零的微观粒子作高速运动,这时粒子物质波的波长 λ∷与速度 v有如下 (B)λ ∝ +∷ ⅡⅡ冫λ∝ 罗意波长是: 4.α 粒子在磁感应强度为 B的均匀磁场中沿半径 R的圆平 轨道运动 ,则 α粒 T搀罕t 、 . 、 ˉ 波长是: ∶ ` ,¨ ‘/ (「J) (A)h/(2eRB) Rb-噼 (C)1/(2eRBh) (B)h/(eRB) (o^1冫 (eRBh) 湍辐|枷 ∷ .-a (D)λ ∝√σ-Ⅴ2 切 -R 弓冫l:' 5· 如图所示,一束动量为P的电子,通过缝宽 -为 a的狭缝,在距离狭缝为R处放置△荧光屏,屏 上衍射图样中央最大宽度 d等于: ⑴等 : ⑴辔 : -.关于不确定关系 AxΔP〓 》“i〓 h/zπ )有 以下几种理解: ˉ ∴ (I)粒子的动量不可能确定。 (2)粒子的坐标不可能确定。 (3)粒子的动量和坐标不可能向时确定。 (4)不确定关系不仅适用于电子和光子,也适 用于其它粒子。 ~ 其中正确的是Ⅱ (A) (1),(2) (C) (3),(4) (:)2;;|: rD,辔 ·Ρ一一 _ 一 D √ P宀 1 (亻 /1' (B) (2),(4) (D) (4),(1) ·37· W纤F 1 C2

二、计算题: L.若一电子的动能等于它的静能,求电子的速率、动量、德布罗意波长。 P=13 moc=473 X10 boms -22 y5c=086c260x02% 70、。144=4X0P 体声债市于身层量申相 2.光子与电子的波长都是0.2m,它们的动量和总能量是否相等?各等于多少?电子 动能为多少? P3.32x0+妇样 不花用品 光子E-196x6=6、2ke/ Y不如丝, n乙✉色好 E-0+1X10 ev=0.t1Mev Eh。t2 =86x°与 C对ho0 58 pime 3.一电子的速率为3×10°m/s,如测定速率的不准确度为1%,同时测定位置的不准确 量是多少?如果这是原子中的电子,可以认为它作轨道运动吗?(△4P,≥)3 aVx=3xo+ 调正不(齿南千净 去 29 2maVk 三人93Xóm 有计干用 原子大小相当 不舶规的作运动
二、计算题: 1.若一电子的动能等于它:的 静能∫求电子的速率 `动 量 `德 布罗意波长。 卜σ浅'|东73ⅪJ·%~/s 冖缸 Ⅱ|回 庇△ f°ⅪD ∷n|永 。 `⒋ ;二 众 '记 /讧 g啪 动能为多少? ∷ ∷ ∶P咄△3冫 ×厅 洋 切-/s叫眸 糍分Ⅱ钅 品舌△亿访 △二∷应 ∥ ^晃 字与电宁的菠苌都嘉⒍zm,它们的动量和总能量是杏相等?各等于多少?电子 3.÷电子的速率为 。×lO° 屮/s,如测定速率的不狼确度为 1%,同 时测定位置的不准确 量是多少?如果这是原子中的电子,可 以认另乞作轨遣运动鸥?(ΔxAPx≥ 罟) 二。辶r/× r。 侈夕=Jj加1/ 冖 :^、 △ - ∶ ∶ ∷ j Zk V× F 3Dˇ。 ‘仵吆 珏◇ 去 ∷ 亠Ⅱ 咴 功慝寻 广:诲g∷ ×广廴 舢 粑当∷∴∷ lW?钥 不角色棚 榀涮 糍 切

:.三 波函数一维定态薛定谔方程(五) 一、填空、选择题: ,裤御 北a还以 1.描述微观粒子运动的波函数为业(,t),则 提,车 型'表示 几华年空 平(T,t)满足的条件是 单弘值有限连独 其归一化条件是 12 2.在一维无限深方势阱中(阱宽为a),当粒子处于波函数中,时,发现粒子几率最大位 置是 ah ;当粒子处于波函数?时,发现粒子几率最大位置是_ Y4,94 3.已知粒子在一维矩形无限深势阱中运动,其波函数为(x)=二 3 a2a t(-a≤x ≤a) A) 那么粒子在x= a处出现的几率密度是 (A片 (B) 洁 4.设粒子运动的波函数图线分别如图(A)、(B)、(C)、(D)所示,那么其中确定粒子动 量的精确度最高的波函数是哪个图? () (B) (C) (D) 5.德布罗意波的波函数与经典波的波函数的本质区别是 惠布去波是九 率技,不是实在袍皇,模为代表紧度 6.将波函数在空间各点的振幅同时增大D倍,则粒子在空间的分布几率 。(变或不变)
波函数 ∷丁维定态薛定谔方程(∶ 五) -、填空、选择题 : 1.描述微观粒子运动的 ΨP中 表示 Ψ(氵 ,t,满足的条件是 2. ,发 蜘 现粒子几率最大位 =器 钔 3.已 1Ⅱ 知粒子在一 维矩形无限深势阱中⒎ 运 Ⅱ 氵 1Ⅱ t (鸬 :UⅠ ) 那么粒子在 x〓 昙 △处艹现的几率密度是 (A)J∶ (:)」 ⊥ (c)l丿言孑 (D)氵吉 量苫陶福l角 ∴∴ 口图(∶ )、 (:)∶ (:∴ ∶|∶ ∴T历 R’ 犁:/A尹∴∶卩 定 鬏 fA》 ∷ -∷ T多 (B) I」L逻芒暹墅Ef尸僵暹 g莲JF时 增大 D倍 ,贝刂粒子在空间 叩 分布几肀 ·39·

二、计算题: 上一维无限深势阱中子的定态波函数为尽血坚。求拉子在x-0到x一号 之间被找到的几率,当 显是数,空发 (1)粒子处于基态时; (2)粒子处于n=2的状态时。 必 P=号4x爱以 的大绿车气速应式,和山是 0、l9b C2) 分2以 水- 0.402 表出级 进公雨 4 2用自由粒于在-维无限深势阱中能量公式B=点(。1,2,…a为势阱宽 度),计算电子(m。=9.1×101kg)在a=10°m的阱中运动时和在a=10-2m的阱中运动 时相邻两能级能量差各为多少?此结果说明了什么? a=16m △E-Fnti-e ctl) m及 -5,么E=nXx0” s fnev =7G4X1ō危/ 之nu1x07J 见业能是可机的连续
二、计算题: 1.一维无限深势 ∷阱申粒宁的定态波菡数为 ψ。 挣 h誓:汆碰亍 在 x〓 o到 x:子 之间被找到的几率,当 、 ` (1)粒子处于基态时; (2)粒子处于n〓 2的状态时。 ∷ ∶ ∶ ∷ ∶ |?PⅡ-允詈丨o|切i- ∷ ∵ ∵ ∷ ∷ 二 丿、t% ∵吁弼碍知垂苏 :L∷ ∶ ∫i廴 Ⅱ∷∷∴Ⅱ ∴ ` ∷ ∷: ’ 用自由粒子在一维无限深势阱中能量公式 E=′ 盘‰“ 亠·i∶ ia坤 阱宽 度)∶ 计算电子(mε 〓9.1× 10卩 kg)在 o亠 iO=⒑m的 阱中运动时和在 a〓 1oˉ 2血 的阱中运动 时相邻两能级能量差各为多少?此结果说明了什么? -`0 β二/o u ˉ. ∷∷Ⅱ ∷ ∷ ∷站△ ∷ ∵∷ ∷∷∴|||f叶i~∵ 粉阜∷轴∷∷ ∷ 茄 y艹 v '2 吁 ro'厶 三=hx人习Ⅺ歹 圬 下 二 Ⅱ40· 'ε彳 田 / l廴d‰ 亠⒕κ。丨ⅪJ,℃ ∶笔彳知硝 J孑L犭石务(。 × 灬 ∥ ∷∷ >⒎ ∷