
第十二章 电磁感应与电磁场 (一)电磁感应的基本定律、动生电动势 一、选择题与填空题:和,运诗业山堂可 1.如图所示,一长为a宽为b的矩形线圈置于磁场B中,而且B随时间变化的规律为 B=B。sinwt,线圈平面与磁场垂直,则线圈内感应电动势大小为: (A)0 (B)abBosinot (C)aboB.cosot (D)aboB d(B.absut b 的欧响 =-wB ab Cosu<o 2.两根无限长平行直导线载有大小相等方向相反的电流I,I以/d的变化率增长 矩形线圈位于导线平面内(如图),则: (A)线圈中无感应电流; (B)线圈中感应电流为顺时针方向; (C)线圈中感应电流为逆时针方向; (D)线圈中感应电流方向不确定。 )的艇袍 丁个 画个<0,gC 3.如图,导体棒AB在均匀磁场B中绕通过C点的垂直于棒长且绕沿磁场方向的轴 00'转动,BC的长度为棒长的1/3,则 A (A)A点比B点电势高; 40 (B)A点与B点电势相等; (C)A点比B点电势低; (D)有稳恒电流从A点流向B点。 4.半径为a的圆线圈置于磁感应强度为B的均匀磁场中,线圈平面与磁场方向垂直, 线圈电阻为R;当把线圈转动使其法向与B的夹角α=60°时,线圈中已通过的电量与线圈 ·23·
第十二章 电磁感应与电磁场 (一 )电 磁感应的基本定律、动生电动势 一、选择乏与填空题: :〓 :。 遢,笙雷 备 军兽】晕晕:章 霎晏 瑙 :l呷l间 变化的 匙 2.两根无眼长平行直导线载有大小相等方向相反的电流 I,I以 dI/dt的 变化率增垦t^ 色 二 -4男 ← = 一 乞铂幽佝 二 '∞ 乳αb‘磅训Γ勺o 绘Q △ 3.如 图,导 体荦 AB在均匀磁场 B中绕通过 C点 的堇 豇 个 c乇 o'怊 C冫 00′ 转动,BC的长度为棒长的 1/3,则 l[长 且 帚 沿 阝 场 :猡 (A)A点 比B点 电势高; (B)A点与B.点 电势相等; (C)A点 比B点电势低; (D)有稳恒电流从 A点流向B点。 4.半径为 a的圆线圈置于磁感应强度为 言的均匀磁场中,线 圈平面与磁场方向垂直, 线圈电阻为 R;当把线圈转动使其法向与 B的夹角 α〓ω°时,线 圈中已通过的电量与线圈 ·23· }lbIΙ 亠 矩形线圈位于导线平面内(如 图)P则 : (A)线圈中无感应电流; (B)线 圈中感应电流为顺时针方向; (C)线 圈中感应电流为逆时针方向; (D)线圈中感应电流方向不确定。 I ^ · -ˉ - -ˉ … · ˉ ˉ ˉ ˉ I ·Ω吲 )q钢平书南 ^亠 ' x B 阝 x x -a 丬

面积及转动的时间的关系是 (A)与线圈面积成正比,与时间无关; (B)与线圈面积成正比,与时间成正比; (C)与线圈面积成反比,与时间成正比; (D)与线圈面积成反比,与时间无关。本基為( 5.如图所示,直角三角形金属框架abc放在均匀磁场中,磁场B平行于ab边,bc的长 度为l,当金属框架绕山边以匀角速度w转动时,bc回路中的感应电动势ε和a、c两点闸 的电势差U。-U。为 (A)ε=0, U,-U.=2Bo 版愈顺,直 4d红(0 (B)e=0, U,-U.-Bot (C)g=B U.-U。=2g呢 (D)g=BoL U,-U.=-ZBae 50a 6.如图所示,一直角三角形abc回路放在一磁感应强度为B 的均匀磁场中,磁场的方向与直角边ab平行,回路绕ab边以匀 B 角速度w旋转,则ac边中的动生电动势为 上wB整个回路 产生的动生电动势为0 30°/1 向太滑长新中动a业 宝不向式考中边'中腿是 0> 7.两根平行金属棒相距为L,其上放一可自由滑动的质量为m的金属杆b,在两棒的 同一端接一电动势为ε,内阻为R的电源,忽略金属棒及b杆的电阻,把整个装置放在磁感 应强度为B的匀强磁场中,忽略摩擦,则山杆滑动的极限速度V。 A(A 影-景6-u叫 皮兴器 X 己量年服中联记0 1-2y 公Y ·24· P F4 是(6820 too V→/BL
面积及转动的时间的关系是 (A)与线圈面积威正比,与 时间无关; (B)与 线圈面积成正比,与 时间成正比; (C)与 线圈面积成尿比,与 时间成正哔; (D)与线圈面积成反比,与时间无关: 5.如 图所示,直角三角形金属框架 曲c放在均匀磁场中,磁 场 言平行于 ab边 ,bc的 长 度为 J,当 金属框架绕 曲边以匀角速度 ω转动时,abc回 路中的 雩:电 动势 ε和 ∷∶F犀月 的电势差 U:-Uc为 ⑴ε=0,叽 -Uc⒎÷卩够∷ ⑴ε-0,订⊥说=-扣Ⅱ t。 ∶±o吒 叽-Uc专。眵 (D)ε =BCⅡ0, 叽-Vc∵ 护¢ 冷 ) 6.如 图所示 ,一直角主角形 曲c回 跨放在一哔 感应犟 度汐 B ∷ ^。 两根平荇金肩棒相距为 L,其上放∵可自由滑动的质量为 m的金属杆 曲,在两棒的 同△龋接一电动势为 ε,内 阻为 R的 电源 ,忽 略金属棒庾 曲 杆的电阻,把整个装置放在磁感 应强度为 B的匀强磁场中,忽略摩擦,则 曲 杆滑动的极限蘧皮 γ∴ ~钅按←丁工^° ︱ ︱ ˉˉ︱ ︱ 丨 ︱ 丶 扛 丨 ▲ E且r{ 阢 `一入 } x x x ∷ˇ Γ Γ ‘ ▲ ΤIIIⅠ I 一B· κ κ x ·24·

8.由导线弯成宽为a高为b的矩形线圈,以不变速率v平行于其宽度方向从无磁场空 间垂直于边界进入一宽为3的均匀磁场中,线圈平面与磁场方向垂直(如图),然后又从磁 场中出来,继续在无磁场的空间运动,试在附图中画出感应电流【与时间t的函数关系曲 线,线圈的电阻为R,取线圈刚进入磁场时感应电流的方向为正向。(忽略线圈自感) IX××1 86y 奇奇 二、计算题: 1.一导线被弯成如图所示形状,acb为半径为R的四分之三圆弧,直线段0a长为R,若 此导线放在匀强磁场B中,书的方向垂直图面向内,导线以角速度。在图面内绕0点匀速 转动,则此导线中的动生电动势e等于多少?电势最高的点是哪一点? X 丽金(A B :向 0b=5R 寸xi)走二-茎gw心 0点电势高 0 +( ·25·
8.由导线弯成宽为 扩高为 b的矩形线圈,以 不变速率 v平行于其宽度方向从无磁场空 间垂直咖 ÷宽为 3a的均匀磁场申,线 圈平面与磁场方向垂直《如图);然后又从磁 场中出未,驻嬖在无磁场申牢间运动,枣在附图中画出感应电流 I、 卢 时日△叩∴甲攀*/gx曲 线,-电 Ⅱ为 R,取线圈刚进人磁场时感应电流的方向为正向。(忽 略线圈自感) b口 a ∷〃。 x xi △ 盖」驷 =、 计算题 : ∶ ~.. 1.一导线被弯成如图所示形状 ,a。b∷ 为半径为 R的 四分之三圆弧 ,苴线段 0a长为 R,若 此导线放在匀强磁场 扌中j的方向垂萱囱亩向内,卓线以角沫度 ω在囱茴内绕 0点匀速 转动,则此导线中的动生电动势 eL等于多少9电势最嵩的点是哪一点Ⅱ △ ∴ X∶ ` 丫 ∴ ∷ ∷ : 一 ∷ -∶ k∴ |Ⅱ ∷∷ ∶沙b≡ '拒 ≡R Iκ × X I ∷ rˉ 丨a` 纟ˉ攵 1σJo锭 ~亻P泄 ′) 、 夕点‘断聆拓 铮 绐t · 笏 ·

2.载有电流I的长直导线附近,放一导体半圆环MN与长直导线共面,且端点MN的 连线与长直导线垂直,半圆环的半径为b,环心0与导线相距a,设半圆环以速度为了平行 导线平移,求半圆环内感应电动势的大小和方向以及MN两端的电压UM-Ux。 米出中游 中的周维到 &nN- atb 2万 a dE=(VxB N-M =虹bdn0 2T(a-bcong MoLV atb MoIVb dlase 八MWF -Eh= 上开 2 a-bo88 3如图所示一无限长直导线上,通过稳定电流L,电流方向向上,导线旁有一长度为L 的金属棒,绕其一端0在一平面内顺时针匀速转动,转动角速度为®,0点至导线的垂直距 离为o,设直导线在金属棒旋转的平面内,试求: 小方向; (A)当金属棒转至与长直导线平行,且0端在下,如图中OM时,棒内感应电动势的大 3T 《(B)当金属棒转到与长直导线垂直,且0端靠近导线,即图中ON位置时,棒内的感应 电动势的大小和方向? 。a,AGC可x)记 二N Ch Eon=SoLide C8) wr-n)dy 2n分4e nite 47 行20 6 4单)w 0->M ·26· w⑦o 2T C以-长) 0>
∷ 2.∷ 载有电流I的长直导线附近,放一导体半圆环MoN与长直导线共面,且端点ⅡⅢ的 连线与长直早线垂直,半 圆环的半径为b,环心0与导线相距a,设半圆环以速度为氵平行 导线平移:求半圆环内感应电动势的大小和方向以及MN两端的电压UMˉ jk∶ Ⅱ c肛/∷ 亻竿幺锆 ' 离为 %,设直导线在金属棒旋转的平面内,试求: 轭 方苫?当 金属棒转至与长直导线平行,且 0端在下,如 图中 0M时 ,棒 内感应电动势的大 u+b (B)当金属棒转到与冬直导线垂直,且 0端靠近导线,即 图中oN位置时,棒 内的感应 势的大小和方向? 6丿xl[},o JHJ 冤 浊 Ν ω 一一 〓 `\丶L` Μ ˉ"〓 廴 一 投 ο `' 丬· 卜ˉl丨 卜 丨 卜丨 民 燕· C浊 GA/9£。胚= ∞抄召洗已 C丬3’ 铴二彳‰夂n‰r ‰ ‰ 冫彡 厶 ,韧 。26· ≥ <缨 迈 △ 丌 叮琥隼箅D ,-冫∥ 〓 卜 ¨ ≡ "μ ι "μ 卜 ☆ 〓 C1t-
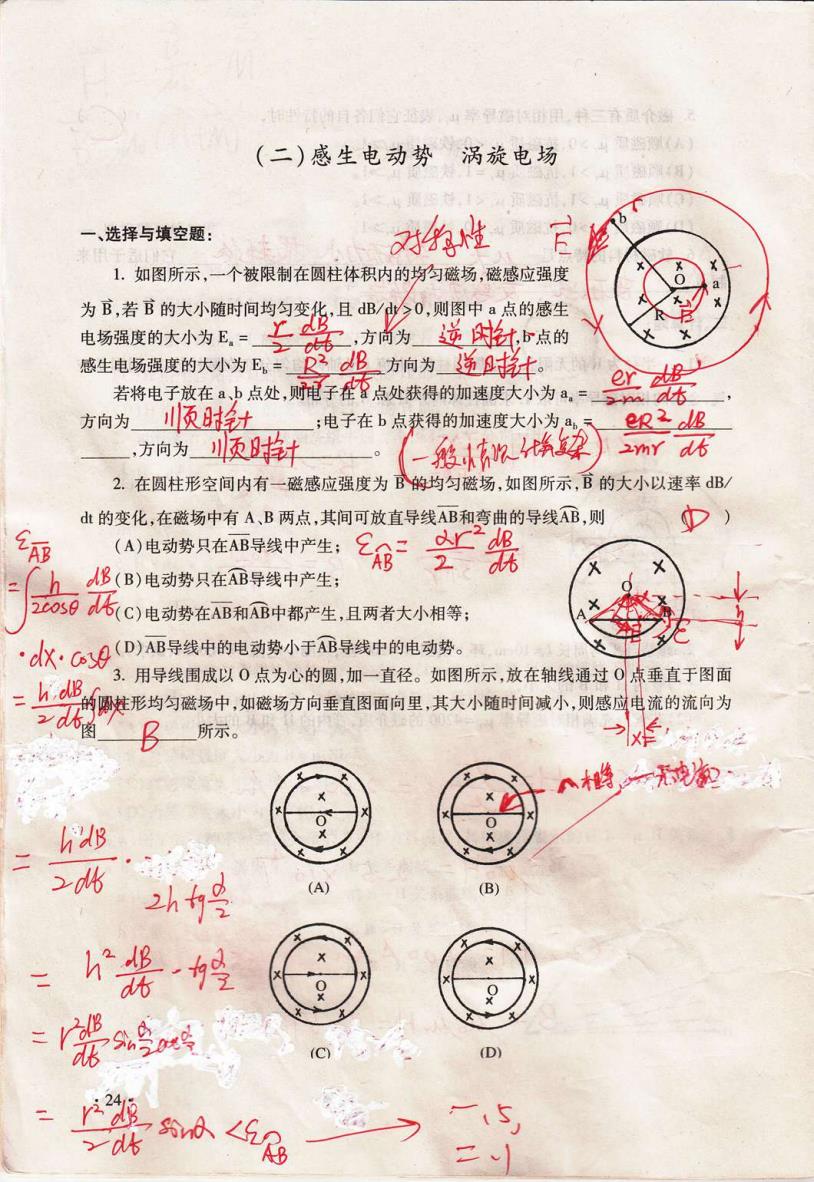
山率每路医街甲,持三通无 (二)感生电动势涡旋电场 一、选择与填空题: 财的性 1.如图所示,一个被限制在圆柱体积内的均匀磁场,磁感应强度 为B,若B的大小随时间均匀变化,且B/0,则图中a点的感生 电场强度的大小为E,=上经 ,方尚为 逆b点的 感生电场强度的大小为E,÷B方向为逆斜。 er alp 若将电子放在a少点处,则子誓点处获得的加速度大小为,=还 方向为 顺时陆 电子在b点获得的加速度大小为a ep2IB ,方向为小顷针 欢 mr d 2.在圆柱形空间内有一磁感应强度为B的均匀磁场,如图所示,B的大小以速率dB/ d山的变化,在磁场中有A、B两点,其间可放直导线AB和弯曲的导线AB,则 少) 刚 (A)电动势只在AB导线中产生; 6器 B(B)电动势只在B导线中产生; 2058 6(C)电动势在AB和中都产生,且两者大小相等: ·d水:C9(D)AB导线中的电动势小于B导线中的电动势。 3. 用导线围成以0点为心的圆,加一直径。如图所示,放在轴线通过0点垂直于图面 二上5的延形均匀磁场中,如磁场方向垂直图面向里,其大小随时间减小,则感应电流的流向为 所示。 入樽一晚2 B 5 2h妈 (A) (B =紧妈 花g D 翁小LR
-、 选择与填空题 : (二 )感 生电动势 涡 旋电场 劂貅 冖 F 官;l 奴:L∶言::二:Ξ b点获得的加速度大小为,%只 @ρ 廴 伽 镌 :骂 蛋£霸 曩瞿 ,且∶ζ大谑 ; ‰ ___,方 向为」 乱的变化,在磁场中有 A、 口两点,其间可放直导线AB和弯曲的导线m,则 口 ) 扁=¥锟 (A)电动势只在AB导线中产生;£n= 二m导线中的电动势。 ′《 勺圆,加一直径。如图所示 ,放在轴线通过 句垂直图面向里 ,其大小随时间减小 ,贝 刂感 垂直于图面 流的流向为 - — ″丿多口 '冫赭 ∷尸ˇd〓 冫 一≡∷〓〓ˇ句 〓 九 ⒈ 〓 2 (B) 占 △ 许 劳 ' q切 么 一 q 一 二 。荔扣Ⅱ黪咦~ ⒎ 璐 锹 气 ‘C、 fD) 广 `、 彡ˇ l

4.一直长螺线管,横截面如图,管半径为R,通以电流L,管外有一静止电子e,当通过螺 线管的电流I减小时,电子©是否运动?如果你认为电子会运动,请在图中画出它开始运动 时的方向,并作简要说明。 0= 一93k应年0( 逆悦针 线黄卡, 配华一 g 5.在圆柱形空间内有一磁感应强度为B的均匀磁场,如图所示,B的大小以速率dB dt变化,有一长度为。的金属棒先后放在磁场的两个不同位置I(ab)和Ⅱ(a'b),则金属 棒在这两个位置时棒内的感应电动势的大小为 B (A)82=81≠0 (B)e2>81 (C)B20),则闭合回路 abca中感应电动势的数值为千KTR2 ;圆弧c中感应电流的方向是C之山 0 ·25
4.L直长螺线管 ,横截面如 图,管半径为 R,通 以电流 I,管外有一静止 电子 e,当 通过螺 时的方向 要说明。 5.在圆柱形空间内有一磁感应强度为言的均匀磁场,如 图所示,言 的大小苡速率0B/ 山变化,有∵长度为%的金属棒先后放在磁场的两个不同位置I(ab)和 Ⅱ(a′ b′ ),则 金属 棒在这两个位置时棒内的感应电动势的大小为 (A)砀 =ε I≠ 0 (B)ε2)ε1 (c)%(εl (v%∶ 玎:0 (图 Φ识彡圭B九 ‰ 南南x =-=厶 伤 丿争h肠 羟 6.一段导线被弯成圆心在o点 、半径为R的三段圆弧£,浣 ,a,它 们构成了⊥个闭合 回路,翁位于XρY平面内,浣和a分别位于另两个坐标面中(如 图),均匀磁场言沿X轴正 方向穿过圆弧£与坐标轴所自成的平面。设磁感应强度的变化率为Κ(Κ >0),则 闭合回路 aboa中感应电动势的数倬0 ;圆 弧浣中感应电流的方向是 r~◆占 争 -赞 彪淝一 ·25·

7.随时同变化的磁场外面有一段导线AB,设B>0,则在B 上的感应电动势: (A)E=0 (B)ε≠0,方向从B一→A (C)E≠0,方向从A→B 二、计算题:时向到 1.在半径为R的圆柱形空间中,存在着均匀磁场,B的方向与柱的轴线平行,有一长为 1的金属棒放在酸场中,设官的变化率为代为一正的恒量,求棒上感生电动势的大小。 工84-oabo≥希(-8-hb 是hU袋 b 2 =0g 2为袭场B被限制在半径R:Q.10m的无限长圆柱空间内,方向垂直纸面向外,设 隘场以=10T/s的匀速率增加,已知0=号,0a=0b=0.04m,试求等腰梯形导线框d 的感应电动势,并判断感应电流的方向。 S=士0-2a是 的0 oa Cove 2R8-}0a20 6 t CB5) 导 --(0o-43)woi ·26· -o、4bV
蕊魁唧呼T|F|肀早∷唧岢|I巴 (A)ε =0 · (B)ε ≠0,方 向从 B→A ∵ . (C)ε ≠Q,方 向从 A→B ˉ ∷ A‘ ·B ︱ ︱ Ll凵 二、计算题 : ∷ ∶ 1.∷ 在半径为 R的 圆柱形空间中,存在着均匀磁场 9的方向与柱的轴线平行 ,有 一长汐 丨的荃庸捧祆在晔场|,毋 F叩孪华率为等汐丁正的谭量,隶榛△牮牛电动势叩大小。∶ 千 :纭1=‰ G00=∴缶‘亠:硅~) ∶ o芒 Ⅱ|锘 |∶ 亻箬 的无酿长圆柱空间内,方 向垂直纸面向外,设 L,Oa〓 0b≡ 0。 Oz+盅 ,试求等脬梯形导线框乩d 的意应电动势:并判断感应电流幽芳南。∷ /. J ,∶ ∷∷ '∶ ∷ ‘ ~⊥ ^ 亠∷茔尸饣⊥当-· 诼:弁h畏 勰 ·厌 犰q 乞 £L切以乙一 B^ ^ ^∷ X∷ X =甘魂J告 硭膨 |△ 务l凹∷° ∷ ˉ务厶 ∷ 二厂ε钙丹^钸)ˇJv fot孕侈v/ 26·

(三)自感、互感、磁场能量 一、选择题与填空题:观自管个所,陈的同 1.自感为0.25H的线圈中,当电流在(1/16)s内由2A均匀减小到零时,线圈中自感电 动势的大小为: (A)7.8×10-3V(B)2.0V. (C)8.0V (D)3.1×10-2V 2.两个相距不太远的平面圆线圈,怎样放置可使其互感系数近似为零?设其中一线圈 的轴线恰通过另一线圈的圆心。 (A)两线圈的轴线互相平行; (B)两线圈的轴线成45°角。 (C)两线圈的轴线互相垂直; (D)两线圈的轴线成30°角。 3.在一个塑料圆筒上紧密地绕有两个完全相同的线圈aa'和bb',线圈aa'和bb'如图 (1)绕制时其互感系数为M1,如图(2)绕制时其互感系数为M2,M,与M2的关系是( (A)M1=M2≠0. (B)M1=M2=0 (C)M1≠M2,M2=0 (D)M1≠M2oM2≠0 (1 (2) 4.一个电阻为R,自感系数为L的线圈,将它接在一个电动势为ε(t)的交变电源上,设 线圈的自感电动势为ε,则流过线圈的电流为: ( (A)E(t)/R (B)[ε(t)-E]/R (C)[ε(t)+8]/R (D)81/ R 5. 长直电缆由一个圆柱导体和一共轴圆筒状导体组成,两导体中有等值反向均匀电流 I通过,其间充满磁导率为μ的均匀磁介质,介质中离中心轴距离为r的某点处的磁场强度 的大小H= 2开Y 磁感应强度的大小B= 工 磁场能 量密度W。= 2TmY 6.有两个长直密绕螺香,张度及线圈匝数均相同,半径分别为5和2,管内充满均匀 介质,其磁导率分别为山和山2,设:5=1:2,山:2=2:1,当将两只螺线管串联在电路 中通电稳定后,其自感系数之比L,:L2与磁能之比W:W分别为: (A)LL2=1:1,Wn:W=1:1。 (B)L:L2=1:2,Wm:W2=1:1。 ·27·
(三 )自 感、互感、磁∷场能量 -、 选择题与填空题 : 糟打;景寻丨T蝼茗l?I∶E∶ 狃均T军Γ 2.两个相距不太远的平面圆线圈,怎样放置可使其互感 中尸匕 不 繁 洱?为零?设 号 中 的轴线恰通过另一线圈的圆心。 「缓 (A)两线圈的轴线互相平行; (C)两线圈的轴线互相垂直; (B)两线圈的轴线成 笱?角 。 (D)两线圈的轴线成 ⒛°角。 3.在一个塑料圆筒上紧密地绕有两个完全相同的线圈 龃′和 bb′ ,线 圈 狃′和 bb′ 如图 熠 Ι辈 缈 ,如图 y茁畜峄 感 帚 勤 慨 叽 :℃ 的关系是 (D (C)M1≠ M2,M2=o (D)M1≠ M2。 M2≠0 4.一个电阻为 R,自 感系数为 L的线圈,将 它接在一个电动势为ε(t)的 交变电源上,设 线圈的自感电动势为εL,贝刂流过线圈的电流为: (A)ε (t)/R (B)[ε (t)-εL]'R (C)[ε (t)+εI']/R 5∶ 长直电缆由一个圆柱导体和一共轴圆筒状导体组成,两导体中有等值反向均匀电流 I谭过,其间充满磁导叠为 u的均匀磁介质,介质中离中心轴距离为 r的 某点处的磁场强度 献尔丘=牟 瀛应强度 · 品矢示ξ =’ 珏 ˇ 二 ¨ ¨ 丁磊窃磊 (((∶∶∶!~~' (D)ε L/ 量密度 WΠ 6.有 两 个长直密绕邂 氇匝数均相同,半径分别为I釉~管内充满均 姗 匀 介 中通 质 电 ,其 稳 磁 定 导 后 率 ,其 分别 自感 为 系 lLl和 数之 u,设 比L1:△ rI:、 与 =⒈ 磁能 2,u1:u2=⒉ 之比Wml:W衄 1,当 将两只螺线管串联 c 分别为: (A)LI:△ =⒈ 1, W血:w证 =⒈ 1。 (B)L1:Lz=⒈ 2, w耐 :w砣 =⒈ 1。 ·27·

(C)L1:L2=1:2, Wm:W2=1:20 (D)L,:L2=2:1, Wa:Wea=2:1。 宜 二计算题拟链) 1.在一纸筒上绕有两个相同的线圈b和ab',两个线圈的自感都是O.05H,如图所示。 求: (1)a和a'相接时,b和b'间的自感; 反串L-0 (2)a'和b相接时,a和b'间的自感; 顺串L=4,02日 2。一螺绕环,横截面的半径为a,中心线的半径为R,R>a,其上由表面绝缘的导线均匀 地密绕两个线圈,一个N,匝,另一个N2,试求: (1)两个线圈的自感L,和L2, (2)两个线圈的互感M, (3)M与L1和L2的关系。 cDB,hn马L,=g=8S 工 工1 =MoNia' 82n1L2=M 2R I2=MoNia R C2)A1=MB,S二Whn,Z,a M=B2L=MoN Nsa' 工 =2L2 .28· R
(C)L1: L2〓 ⒈ 2, (D)L1:Iz9=⒉ 1, Wm】 : △ `砣 =1: 2。 W龃 :W砣 =2|△ 。 ˉ′ I 同的线圈 ab舶 a′ b`,两个线圈的自感都是0.05H,如 图所示。 求: ~ 终丬 2.一螺绕环,横截面的半径为 a,中 心线的半径为 R,R》。,其上由表面绝缘的导线均匀 地密绕两个线圈,一个 N1匝 ,另 一 个 N2,试求: (1)两个线圈的自感 L1和 L2, (2)两个线圈的互感 M, (3)M与 L1和 L2的关系: ∶ ∷ cD Bi∷。伽 y9|Ξ亠 丿 ='。泓讠廴 猡o-^nrˇ =iF ∠⊥∷△ 和呼 二 亠R 乙冫丿 =盹 Bls⒎-脱办 刀1三`吖 冫R 二几 〃弘 ` (1)a舶 ,碉接莳,b和 ” ′向晶自感;焱↓ ∠△口 ⒓ˇ砰户相 ∶ △ a和 吖间的即 飙 丬丨艮串圩 4铲 饬 沈 ·28· 梁 叫与厶

能招 3.一根同轴电缆由内圆柱体和它与同轴的外圆筒构成,内圆柱的半径为a,圆筒的内、 外半径为b和©.电流I由外圆筒流出,从内圆柱体流回。在横截面上电流都是均匀分布的。 (1)求下列各处的磁能密度0:圆柱体内、圆柱体与圆筒之间、圆筒内、圆筒外; (2)当a=1.0mm,b=4.0mm,c=5.0mm,I-10A时,每米长度同轴电缆中储存多少磁 能? 0K,H,8=s 2T02 Wm= 8mat asreb H6 2Tr,W MI 8T2T2 Wm-Stmdv c7C,H=0,B-0,w-o 4.如图所示,截面积S=1.00cm,平均周长1=100cm的环上均匀地绕有N=500匝线 圈,环内充满均匀各向同性的磁介质、介质的相对磁导率μ,=100。 (A)用定义求环的自感系数; (B)先求磁场能量,再由能量求自感L。 9=ohn江52红 L=Wuuyns=3.14 mH =25o°八0 (WV =tuurn'ties L=4n2=314m月 ·29·
'哪 膨鳕· 3· ˉ烬同轴电缆由内圆柱体和它与同轴的外圆筒构成,内 圆柱的半径为 a,圆 筒的内、 外半径为b和 c.电 流I由外圆筒流出,从 内圆∷柱体流回。车横截面上电流都是均匀分布的。 (I)求下列各处的磁能密度 ωj:圆 柱体内、圆柱体与圆筒之间、圆筒内、圆筒外; (2)当 a=1.0mm,b=4.o叩η,c=5.omm,I=10A时 ,每米长度同轴电缆中储存多少磁 能? ∶ ∷ ∷⑴夂△H孚“ ∶亻豁 丿Ⅲ ∷γ议△H△扣j∷ 。 j”△屁圹 圈,环 内冖满均匀各向同佳的磁介质、介质的相对磁导率 ur=1∞ 。 (^)用定义求环的自感系数; (B,先求磁场能量,再 由能量求 自感 L。 ??¢=‰ 吨‘二红 υ ⒊ 〓⒈ k } ≡ ∷ 〓 " ·一 一一 芷 / ∥ "`二 亠 ∠二 /Ⅱ虍 yLⅡ愆= 3.∫孕h凵 ·29· ∠二 丬冫γ~nsˉ 3:丨 伞η叫 ‘刁 W彡 二功 冫 圭∠ェ·:∷ 劾 r疵比