
第十三章 波动光学 (一)获得相干光的方法 双缝干涉 一、选择题与填空题: 1,相无光满足的条件是① 同板包 ,®日孰姓 ,③ 相义有两束相干光,频率为,初相相同,在空气中传播,若在相遇点它们几何 路程差为2-1,则相位差△p= c-n). 2.光强均为的两束相干光相遇而发生干涉时,在相遇区域内有可能出现的最大光强 是 4To 可能出现的最小光强是 O 3.用白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一纯蓝色的滤光 片遮盖另一条缝,则 ①) (A)干涉条纹的宽度将发生改变。 (B)产生红光和蓝光的两套彩色干涉条纹 (C)干涉条纹的亮度将发生改变。 (D)不产生干涉条纹 4.一波长为λ的单色光照射在一双缝装置上,在屏上产生由暗条纹间隔开的亮条纹干 涉图样,如图所示,则从两缝S,和S2到亮纹P点的光程差为 (A)分 (B) (C) (D)2X 27 X=2 5.试分析在双缝实验中,当作如下调节时,屏幕上的干涉条纹将如何变化? (A)双缝间距变小: (B)屏幕移近: (C)波长变长: A小△X个 (D)如图把双缝中的一条狭缝挡住,并在两缝垂直 平分线上放一块平面反射镜: 明、监发支换一治线
第十三章 ,波·动 :光 学 C一 )获得相干光的方法 双缝干涉 一、选择题与填空题: 1柙歹投灌厍的条仵是① 亻捞 襦薪早疵麟荔茄赢襁 ② 茚痛掩赢齑Ξ♀湎亠 路裢羞另乇 ’ 二i1∶ 页i相位差△♀= -乏孓Cr△'F、 。 孑踮箍均为 IO的 两束相干 箱遇区域内有可能出现的最大光强 是 4L 。可能出现的最小光强是 。 3.用 白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一纯蓝色的滤光 片遮盖另一条缝,则 (A)干涉条纹的宽度将发生改变。 (B)产生红光和蓝光的两套彩色干涉条纹 (C)干涉条纹的亮度将发生改变。 (D)不产生干涉条纹 ∷ 4。 一波长为λ的单色光照射在△双缝装置革,在屏上产 产甲亨罕罕:呷Tl早 最爷 涉图样,如 图所示,则从两缝s`和 s2到亮纹P点的光程羞为 T (冫 ) (A)去 (:)λ (C)÷λ -D)纸 : ∷j∵ 5,试分析在双缝实验中, 诘’ 0i镐 涉条纹:∶∶宙i讠。 冖 冫’ (A)双缝间距变小 : (B)屏幕移近| (C)波长变长I (D)如 图把双缝中的∵条狭缝挡住,并在两缝垂直 平分线上放一块平面 ·30·

6.双缝干涉实验装置中,当光源发生下列变化时,屏上条纹的位置将如何变化? (1)S平行S,S2,联线方向作微小位移:(如图S移到S') (2)S沿垂直S,S2联线方向作微小位移。 不毁 二、计算题: 当9E4的, 1.在双缝干涉实验中,用波长入=546.1nm的单色光照射,双缝与屏距离D=300mm,测 得中央明条纹两侧的两个第五级明条纹的间距为12.2mm,求双缝间的距离。 d=10 Dn/x=0.13m 2.用钠光(入=589m)作杨氏实验,在离双缝1.0m处的屏幕上仔细测量干涉条纹,发 现第20级明纹的中心在距第零级条纹中心11.78mm处。问这两缝间距是多少? 3.在一双缝实验中,缝间距为5.0mm,缝离屏1.0m,在屏上可见到两个千涉花样。一 个有480nm产生,另一个由600nm的光产生。问在屏上两个不同花样第三级干涉明条纹间 的距离是多少? 4X)= 72 ·31·
⒍双缝干涉实验装置中:当光源发生下列变化时,屏 ξ雩斧叩守 覃将如何变化? (1)β 平行 s画 ,联线方向作微小位移:(如 图 s移到 甲sF于享⒎:|产罕歹甲f繁忄产箩。△床鲛 =、 讨算璎:∷ ∷·∷∷Ⅱ∷ ∷∷∶∷Ⅱ∷∷∷∷∷i Ⅰ∷∷∶∷∷ ∷ ∷ ∷ 1.在 双缝干涉实验中,用波长λ〓M6.1nm的 单色光照射,双缝与屏距离p干 sO0血”,测 得中央明条纹两侧的两个第五级明条纹的间距为 12.2mm,求双缝间的距离。 ∶ ∷ 艹 铲 ∷∷ ∷ ∷ ∶ J亠/0 Ot招 ¢ⅡⅡⅡ 2,用钠光(λ 〓ss9nη )作杨氏实验,在 离双缝 1.0血:处 的屏幕上仔细测量干涉条纹,发 现第 ⒛ 级明纹的中心在距第零级条纹中心 I1。 Tgm”处。∷间这两缝间距是多少? 3· 枣∵双缝实验∷申:缝 ∷间跛为 △thm,缝离屏 1.Om,在屏上可见到两个干涉花样。∷ 个有 鲳0nm产生,另 一个由6∞z1m的光产生:问在屏上两个不同花样第三级干涉明条纹间 的距离是多少? ∵ ∶∷ ,刁 丿 ∷丬| P刁|灬二 ∷ L Γ氵 阢 已K9P T ·31·

(二)薄膜干涉劈尖 一、选择题与填空题: 1.光在折射率为n的介质中走过几何路程为r,相当于光在真空中走过门二 路程,把它称为 光程 2.两条相干光a和b,从相位相同的A点和B点传至P点,它们的相差分别等于多少。 空气 (a) (b) 空气 玻璃 (c) (a)△p= 0 (b)A=_ 2T0-)A (c)Ao= Cn)2 3.如图所示,波长为入的平行单色光垂直人射在折射率为2的薄膜上,经上下两个表 面反射的两束光发生干涉。若薄膜厚度为e,而且n,>n2>n3>,则两束反射光在相遇点的 光程差8= 3nze ,相差Aφ=一eA S=2ne (无拨) 一买8 na }-0)g-2eJn2-n24 .二2en2z 4.两块平玻璃构成空气劈尖,左边为棱边,用单色平行光垂直人射。若上面的平玻璃慢 慢地上平积则干涉条纹 () ()向棱边方向平移,条纹间隔变小。 ·32. 8-2dt冯 d个6个
(二 )∷薄膜干涉∴∷劈∵尖 -、 选择题与填空题: 1.光 在折射率为n的介质力魑过几何路程为r,相 当于光在真空中走过 y9r 路程,把它称为 2.两条相干光 a和 -,从相位相同的A点和 B点传至 P点 ,它们的相差分别等于多少: 卜 卜 f。 9 (a)Δ【P= (b)Δ9= (c)Δcp= 3.如 图所示 ,波 长为 λ的平行单 直人射在折射率为 n2的 薄膜上,经上下两个表 卜 }Ⅱ∴p冫eJ Ⅱ卜济邢 甩 ” △吼 ˉ ˉ ˉ ˉ — _水 面反射的两束光发生干涉:若薄膜厚度为 e,而且 nl)n2)瑁 FlIFf∷l∶【 氵 晃程差 s亠 :亠 n冫O ∴ 相差 A【P△ ∷ -Jˉ9 s·2田 ,e 耐 彬 ) 邓 ⒎△紫s∵ 4.两块平玻璃构成空气劈尖,左边为棱边,用单色平行光垂直八射。若上面的平玻璃墁 ·32· ∶则干涉条纹 S讠 蚓唣 洗个 召个 (((∶∶!∶∶J

(B)向棱边方向平移,条纹间隔变大。 0理某图 (C)向棱边方向平移,条纹间隔不变。 (D)向远离棱边的方向平移,条纹间隔不变。 (E)向远离棱边的方向平移,条纹间隔变小。 5.如图所示,两个直径有微小差别的彼此平行的滚柱之间的距离为L,夹在两块平板玻 的中间,形成空劈尖,当单色光垂直人射时,产生等厚干涉条纹。如果滚柱之间的之 L变小,则在L范围内毛涉条纹的 (A)数目减少,间踵变大。 (B)数目不变,间距变小。 候补)数目增加间野变个 (D)数目减少,间距不变。 长 二、计算题: 1.在折射率为n=1.68的平板玻璃表面涂一层折射率为n=1.38的MgF,透明薄膜,可 以减少玻璃表面的反射光。若用波长入=500nm(1nm=10’m)的单色光垂直人射,为了尽 量减少反射,则MgF2薄膜的最小厚度应是多少? ↓↓ MgF 玻片 2买2冰13-+DT 22人8≥可 、Cn>38) 纳9058nm ·33
〈B)向 棱边方向平移,条纹河隔变大。 ∷ ∷ ∶∷∷.∷ ·∷ ∷ ∷ ∷ ∷ (C》向棱边方向平移:条纹间隔不变。|∷ ∶ ∶∷ ∷ ∷ (D)向远离棱边的方向平移∫条纹间隔不变: ∶∷∷∷∶∷∷ ∷∷ ∷ ∷ (E)向 远离棱边的方向平移,条纹间隔变小。 ∷ 5.如 图所示,两个直径有微小差别的彼此平行的滚柱之间的距离为 △,夹在两块平板玻 璃的中间,形 ,当单色光垂直入射时 ,产生等厚干涉条纹。如果滚柱之间的距 L变小j则在⊥ (A)数 目减少 ,阃 (B)数 目不变,间距变小c (D)数 目∷减少,间距不变。 条纹的 ’ 簟 硎 ∷弩:l罩·!∴ 甲 `t3 f` g箩 变小。 刂∴∶ 二、计算题: ∷∷∷∷∷ ∷ ∷∷∷∷ |∷ ∷ ∷ 量 以 Ⅱ 减 减 少 少 钞玻 反 璃 鼢 科表 :负 肀面 ⅡM查 汐的 ∷ F∶ 反 |丁 射 薄 ⒈ 光 膜 |呼:若 的最 用 小 咿波 厚 长 度 睁 应 λ=5∞ 是 |‰ 多少 】 ? γT瑟姆 ∷ 蕊搬 硝絮 哂 一∷∷ ⒉丁 一 刀 t.引 :i而|匕△Dt 毛干1艹 ^亠 y|t 刀 丿 亻h 0叨 >∫ ′丿′》 △ 御 甲。`夕 ′冖即 ·33·

2.为了用光学方法精确测定某金属丝的直径,将细丝夹在两块光学玻璃片之间,形成一 空气劈尖,如图所示,用单色平行光垂直照射劈尖。已知入=632.8m,测得L=20.00cm,第 K级明条纹与第K+10级明条纹的间距b=80.00mm,求细丝的直径d。 25分9 80.0nSn0 6328 1o 2 S分0=}955x7ò 9时x希d4607.9划 3.有一劈尖,折射率为1.4,夹角0=10-4rad,在某一单色光垂直照射下,可测得相邻两 明条纹之间的距离为0.25cm。试求: (1)此单色光在空气中的波长; 7oonw (2)如果劈尖长为10.5cm,那么总共可出现多少条明纹?1b℃0.)心 42 0、25C2 2分0X1小4 刀700M○ 753- ·34·
⒉为了用光学方法精确测定某伞属丝的直径,将细丝夹在两块光学玻璃片之间,形 成一 空气劈尖,如 图所示,用单色平行光垂直腮射劈尖σ已知入△“|忠 nm,测得L=?⒐ .00。m,第 K级明条纹与第:Κ +IO级明条纹的间距b=叩 .00叩”,求细丝的直径d。 ∵ ∷∵ ∷ 彳| 乡ρcoDⅡ /° `S枥 = 矢切|冫 四忙邦矿 3,有 一劈尖 ∷ ,折射 率为 1.⒋ 夹 ∷ 角 ⒍亠lO“ rad,在豇某筵一单嚣色光霪垂直藿诬蕊 T皂 黼 1桌溉沪 σ扛 ,胁 Ⅱ∷-/D·私 4℃∶ 刁 D、 ⒉tC认、乙 a`〃 △引b胪 κ/许 °¤ -∶… ∷ ·34·

(三)牛顿环 迈克逊千涉仪 一、选择题与填空题: 1.若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬人折射率为33 的水中,则干涉条纹 (A)中心暗斑变成亮斑。 (B)变疏。 (C)变密。 (D)间距不变。 2.如图所示,平板玻璃和凸透镜牛顿环装置,全部浸入=1.60的液体中,凸透镜可沿 00'移动,用波长入=500m的单色光垂直人射。从上向下观察,看到中心是一个暗斑,此村 凸透镜顶点距平板玻璃的距离最少是 (A)78.1nm (B)74.4nm (C)156.3nm (D)148.8nm (E)0 无羊油换】 n=1.68 S2hd=至,h=l6 F”=1.60 n=1.58 d飞79h lo 3.如图,用单色光垂直照射在观察牛顿环的装置上,当平凸透镜向上缓慢平移而远第乎 面玻璃时,可以观察到这些环状干涉条纹 (A)向右平移。 单色光 (B)向中心收缩。 (C)向外扩张。 (D)静止不动。 (E)向左平移。 4.在观察牛顿环的实验中,平面透镜和平板玻璃之间为空气时,第10个明环的直径为 1.40×10-2m,其间充以某种液体时,第10个明环的直径为1.25×102m,则此液体的折射 率n= 2 o-pro 5.迈克尔逊干涉仪可用来测量单色光的波长,当M2移动距离∠d=0.3220mm时,测得 陕单色光的干涉条纹移过△m=1024条,该单色法铲长2一 △h .33.1
(i三 〉牛顿坏 迈克∷逊干 涉仪 -、 选择题与填空题: |尔 FⅠl干l∶∶∶】;1鹑l∷尹:):∷∶F箪↑ 圻 l率戊。£LI (C)变密。 (p)间距不变。 爝 酆 辚 锣 早↑℃∷↑FFl?幂 ∶∶ l?景∷↑军唧 Ι ∷ ∷ (^)74.4nm (C)“J血 ″ ∷ ∷ 丨 | | 龀Ⅱ ∷群 ∷龇 } 毯。痴以土各,” 二Ⅱ∷∷ ∷仁螽 t7″h汪 秀严那干呀条娣|兮 Ⅱ丫罕珲遏z墅 z△卜 猡 1.6仑 亩嵌皋#鎏卣露量霉 s旱馔窭搴IT:笨帚÷ ∴亨TˉF镜l∶[幂 ∷Ⅰ子 硒专3 (B)向 中心收缩。 ∷ ′ (C)向 外扩张。 ∵ ∷ (^)静止不动。 ∷ (E)向 左平移。 ∶ ⒋在观察牛顿环的实验中,平 面透镜和平板玻璃之间为空气时 ,第 10个 明环的直径为 1.扪:× 1oˉ ∶m,其间充以某种液体时,第 10个 明环的直径为 1|z~s× 10ˉ 缍 ,则 此液体的 率n〓二 |.冫r 姑慈癫旒谴巍古函菝轳鳊:{ζ∶吉f丨:i营;P络3”‰确酷犁 丨.冫r ∷ ∵ I ∶ 哆%饣 Fcr沪 当》R 吒 砂 奄 气 丨 〓 ·33·∷和
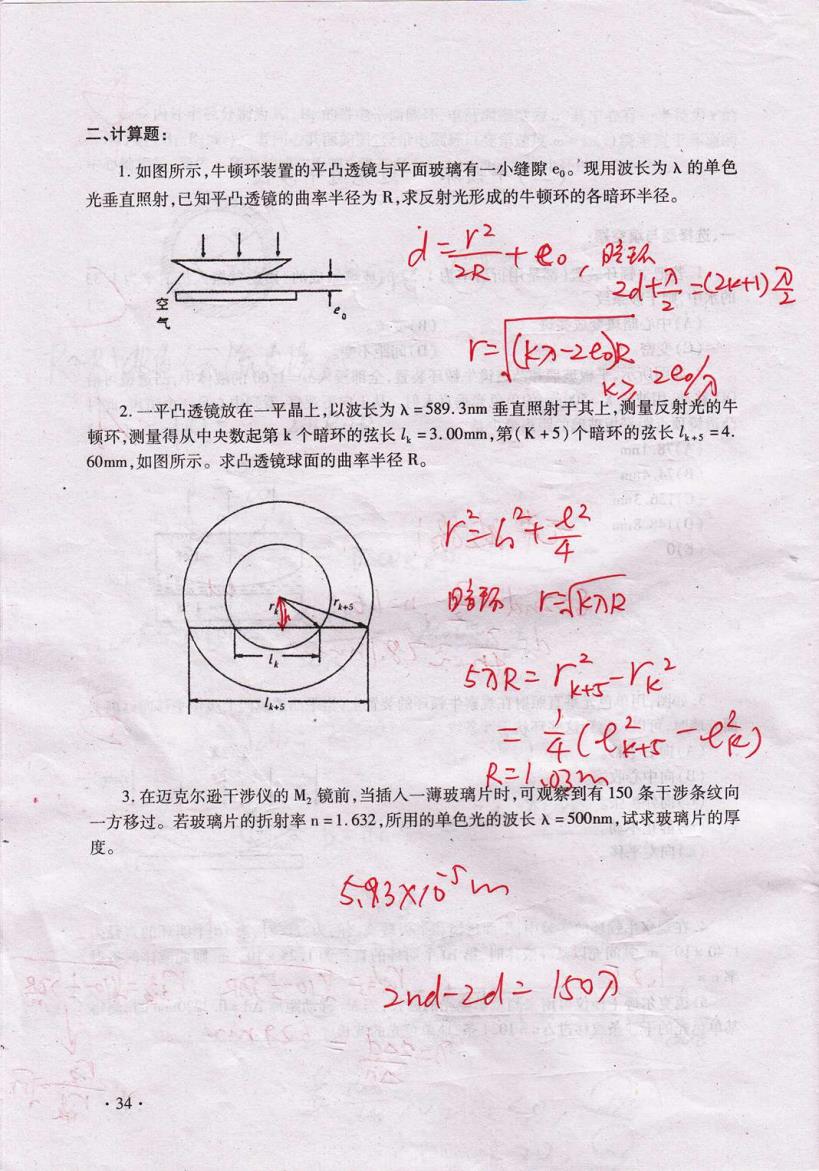
二、计算题: 1.如图所示,牛顿环装置的平凸透镜与平面玻璃有一小缝隙。'现用波长为λ的单色 光垂直照射,已知平凸透镜的曲率半径为R,求反射光形成的牛顿环的各暗环半径。 十eo,脱认 2t2-(24)2 r-( 2.一平凸透镜放在一平晶上,以波长为入=589.3m垂直照射于其上,测量反射光的牛 顿环,测量得从中央数起第k个暗环的弦长1,=3.00mm,第(K+5)个暗环的弦长人+5=4。 60mm,如图所示。求凸透镜球面的曲率半径R。 r+¥ 03 3孙n2 snB=Ts-re 三 4(er一e 在近克你干涉仪的锁前,当插人一薄玻璃片司梁到省50条于涉条纹向 一方移过。若玻璃片的折射率n=1.632,所用的单色光的波长λ=500m,试求玻璃片的厚 度。 S93x/6' 3nd-2d-1507 ·34·
二1计 算题: ∷ 1.如 囱fJF示 ,牛顿坏装置的苹凸透镜与平面玻璃有工小缝隙 。。。 ’ 现用波长为 λ的单色 光垂直照射,已 知平凸透镜的曲率半径为 R,求反射光形成的牛顿环的各暗环半径。 叫⒆乇泶⒊0% 2.一平凸透镜放在一平晶上,i以 菝丧为λ⊥080?。 n访 堇叠琅射车直~f扁瞿髭毛轷姥线牛 顿环:测量得从中央数起第k个暗环的弦长Jk〓 g。 OOmm,第 (K+5)个 暗环的弦长 `k∶ ∶=4. ∞血m,如 图所示。求凸透镜球面的曲率半径R。 F》冖苔 J9|刂 ;ˉ冫彳廴·;∶ ∴饵陌亓p t^专 o七 乙艹∷-。c锄 3.在迈克尔逊干涉仪的 M2镜前,当插人△薄玻璃轱 告瀚 ij0基+痴森纹向 一方移过。若玻璃片的折射率 n|1,“2,所用的单色光的波长 λ=5∞n【n,试求玻璃片的厚 度。 ∴ 翎b不 /-Ⅱ 苦∷△r%Ⅱ垃 丿· · ∷一一灬 〓 〓〓〓 二 ∷〓 胥 呢 〓一一一~一≡ ∷ I⒎ 夕 ·34· i砌.⒉爿·“刁

(四)单缝衍射 公 一、选择题与填空题: 1.波长为λ的单色光垂直射照单缝AB上,在屏幕上形成衍射条纹,若AP和BP二条光 线的光程差为3.5λ,则 (A)P点处在第 级 纹上 (B)OP间有 条暗纹 (C)单缝可以分成 个半波带。 (D)若衍射角φ增加,则单缝被分的胖波带数目 时,每个半波带的面积 相应明纹亮度 2.平行光垂直射于单缝,观察夫琅和费衍射,若屏上P点处为第二级暗纹,则单缝处波 阵面相应地可划分为 半个波带。若将缝宽度缩小一半,P点将是 级会 纹 3.在单缝衍射实验中,若将单缝向上有一微小平移,则屏上的衍射条纹将: (A)向上平移; (B)向下平移; (C)不移动: 4.惠更斯引入 子波 的概念提出了惠更斯原理,菲涅耳再用 迫相4 的思想补充的惠更斯原理,发展成惠更斯一菲涅耳原理。 5波长为入的单色平行光,经圆孔(直径为D)衍射后,在屏上形成 园人 形状的明暗条纹,中央亮斑叫 ,根据瑞利判据,圆孔的最小分辨角δ= 227少 6在迎面驶来的汽车上,两盏前灯相距120m,则在汽车离人94.8洛的地 方,眼晴恰可分辨这两盏灯。(设夜间入眼瞳孔直径为5.0mm人射光波长入=550@m义。入 h 二、计算题: 1.波长为500mm的平行光垂直地人射一宽为1mm的狭缝,若在缝的后面有一焦距为 100cm的薄透镜,使光线会聚于一屏幕上,试求:第一级明纹的位置,第二级暗纹的位置,中 ·35·
′ (曲 )单缝衍射 -、 选择题与填空题: ⒈波长为 λ的单色光垂覃射照单缝 AB亠 ,在屏幕上形成衍射条纹,若 AP和 BP二条光 ( ) T艺珲蜃莒£瑾鋈 级 维上 {己 `葬痴: {乏 孺ξ童土:蹴’ 蟹嬲 娆骺辖瞰蹁 2.平行光垂苴射于单缝, 察夫琅和费衍射,若屏上 P点处为第二级暗纹,则 单缝处波 阵面相应地可划分 半个波带。若将缝宽度缩小∵半,P点将是___ 明暗条纹,中 央亮斑叫 J根据瑞利判据 ,圆 孔的最小分辨角 δ♀= 纠 D∷ 三上俩聋煎坷相距⒓0cm,则 隹汽车苒人△乇汪免 =纽 L珲了枷蚺 方,眼睛恰可分辨这两盏灯。(设夜间人眼瞳孔直径为⒋ 0盂m入射光波长 λ=ss吲至蜘 |泛 P/D钅 丿、0伍六 饧 幻1伍血的狭缝,若 在缝的后面有一焦距为 100cm的 薄透镜,使光线会聚干△屏幕△,试求:第 ∵级明纹的位置,第 二级暗纹的位置,中 ·35· 3.桎单缝衍射实验中 ,若将单缝向上有一微小平移 ,则屏上的衍射条纹将 : (A)向 上平移; (B)向 下平移 ; 的思想补充的惠更斯原理 ,发展成惠更斯一菲涅耳原理。∷ `1厂 -ε ∶獒 l父 :⊥⑾硅 =勰i熄画法∷耷:艹舞F铂 玉坤垒幽子

央明纹宽度 aclm) 0明服ng-土C+D子 %经人S分-土明 四最,x6仁盗 k>2%】 =22X2中 美边 2.今有白光形成的单缝夫琅和费衍射留样,若其中某一光波的第3级明纹和红光(入= 600m)的第二级明纹相重合,求此光波的波长。 2 72= 5刀 20 3.如图所示,设有一波长为λ的单色平面波沿着与缝面的法线成山角的方向人射于宽 为a的单狭缝AB上,试求出决定各们射喑纹的行射角甲的条件。 B AB间光程差 △6-5P-SE 车他等数N 0=2K 纹 ·36… 瓷+%座
疝Ⅶ 景 p瞰 冖贮 ∵亠 。 wZ+沂 帏珈 次冖卢色当吩 ∷ 冖眺f∴ 冫|锾∴艹玩¢△:娑 ^糕糍乡乩辘`|∶{∶∶∶;;i∶ 矗赢 坛勰辐碱 唛缶蕴砝篆繁 ·l) 2⒉∶∷×△塄 b四彦 Ι翅 咚廴.勤 呷屮甲罕甲叩缪相酰眇桫屮呷~∷∷ˉ 卫 ∴ 匀 . 热 ~~Σ》J ⒊赢麻磕乒蒎嘉艋 济赢瀹赢赢嬷ⅡⅡⅡ”艹 为a的单狭缝姆 上,试求出决定各极小值的彳 . ∶ ∶∷∷ ∷ ∷ ∷∷ ∴∵_∷ ∷-∷ ∷/?F∶∫∶ ∵∷∷Ⅱ钾△ ^∷ ∶ ∷∵ =∷ 彳∷鹾Ⅱ锪∷ J⒉ F (`∴:∶|∵ ζ甘o哆ˉr∴W ∮ a ∷叩邺∷田 `么 t‘ 终卵如 厶S△ 丬9′ i平 ÷fⅡ狎)

(五)光 栅 一、选择题与填空题: 1.光栅衍射公式(a+b)sinp=±K,当K=0,1,2,…等整数值时,两相邻狭缝沿p角 折射出的光线能够互相加强,试问: (1)当满足上述条件时,任意两个狭缝沿φ角射处的光线能否相互加强」 能 (2)在上式中,当K=2时,第一条缝与第二条缝沿φ角射出的光线在屏上会聚于第二 级明纹处,则两者的光程差是 20 2.波长λ=550mm的单色光垂直入射于光栅常数d=2×104cm的平面衍射光栅 能观察到的光谱线的最大级此为 (A)2 (B)3 (C)4 (D)5 ,3.用波长为589.3nm的钠黄光垂直人射在每毫米有500条缝的光栅上,求第一级秋 大的衍射角。 (A)21.7° (B)17.1° (C)33.6° (D)8.4 4.一束白光垂直照射在一光栅上,在形成的同一级光栅光谱中,偏离中央明纹最远的是 D (A)紫光 (B)绿光 (C)黄光 (D)红光 5.若光栅的光栅常数为(a+b),透光缝宽为a,则同时满足(a+b)sinp=K入和asino= K时,会出现缺级现象,如果b=a,则光谱中缺2上上斗22级。如果b=2a,缺 3 6.一束单色垂直入射在光栅上,衍射光谱中共出现5条明纹,若已知此光栅缝宽度与不 透明部分宽度相等,那么在中央明纹一侧的两条明纹分别是第 级和第 级谱线。 7.设光栅常数为d,波长为入,当单色光与光栅线夹角为9斜射时,通过相邻二缝的1 光和2光到P点的光程差如图(g所,9t免公政写为乱分平+dsh6 如图b所示6=d5处单二C2政为in中-g02二土7 ·35·
(五)光 栅 -、 选择题与填空题: ⒈光哪衍射公本(0+-)|n,.± Kλ ,当 阝|%∶ I,?,∴ 等整数值时,两∷相邻狭缝沿 ♀角 折射出的光线能够互相加强:试 问{ (1)当 满足上述条件时,任意两个狭缝沿 ∶ ,(2冫 在上术中:当 Κ=2时;第工条缝与第 挚r爹狯臂〖詈彗甘譬罩蘩繁啻言肓下f|卩罗阝繁∷dγ ′ ∴?∶∶∶咖的平甲tγ半 能观察到的光谱线的最木级此为 貊 ′′ ∷ (A)? (B)3 (C)4 ∶∵∴(D)5 工 ∷ ∶ ∷. 本叩衍射 最1。 ∶ ∵∶ i;∶IlF1帚帚:ll罕 帚忄有 VQ绎竿的 I芈十 ’求第一 繁芷考 6° (D)⒏ 俨∵ ∴ 丨:l;光F氢llI∶丨 栅 ifζI的 同 丁繁 光 呷 光谱中,偏 离中 十 明纹最 干罗景 (D)红光 旦莒6.ˉ i量 束 I莒鐾棠釜景爹丰;f早罩翠耻I≯罂]∶晕虽罩|射糕足罗,褒∶三 单色垂直人射在光栅上,衍射光谱中苯出现5条明纹,若 已知 光栅缝宽度与不 透明部分宽度相等J阝 么在中央明纹一侧的两条明纹分别是第 级和第 级谱线。 ·35·