
第六章 机械振动 (一)简谐振动 下、填空、选择题: 1.一简谐振动,在t=0时xy ·19·
第六章 机械振动 (一 )简 谐振动 动,在 t=0时 x(0,v(0,那么表示简谐振动的旋转矢量图为 (冫 谐振动的弹簧振子9振 幅为 A,周 期为 T,其振动方程用余弦函数表 ,质点的状态分别是: x=鸬 山SC1笋 t中) 向正向运动; (3)过 x〓 告 向负向运动; 处和正向运动 ; (4)过 xJ多 则相应的初 3丌 3.质量为 10 10冖 kg的小球与轻弹簧组成的系统,振动方程为: x〓 0.1cos(8π t+钅|π ) (sI) 则 圆 率ω--/8可 ρ濉 ,周 期T=~沙沙冫`亠ssgs ,振幅A〓 丿、l` ,初 L 浔帚:∶ 严 丿辶 卩 旧迈簋崖芝嘛 = =二 ‘;、 ΞLη“F冖 ‘∞ β¢ 梵ˉ 戽协 F'/L-“〃形氟∷F ` o,亻}l.,画 肛、 `ω (1)xO〓 -A ·19
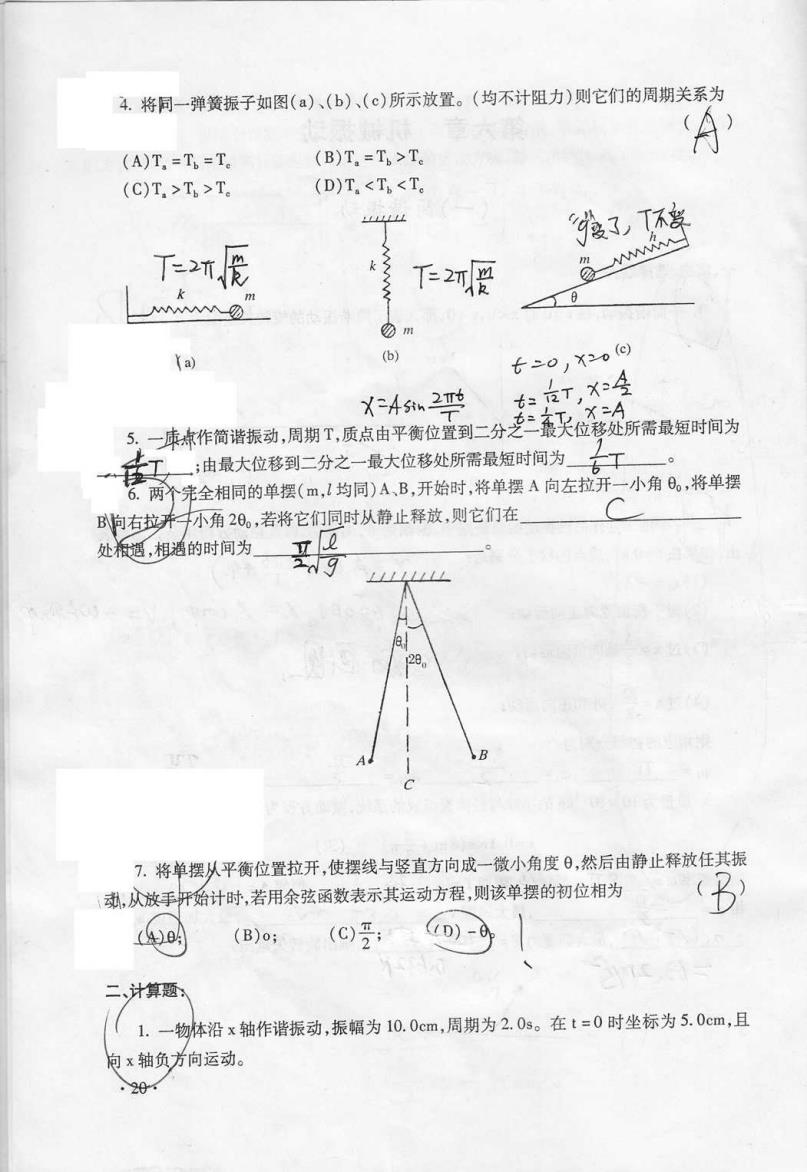
4.将同一弹簧振子如图(a)、(b)、(c)所示放置。(均不计阻力)则它们的周期关系为 A (A)T,=Tp=Te (B)T,=T>Te (C)T.>T>T. (D)T <T<Te 线3,不特 下辰 下2河受 w ⑦m (a) (b) 七二o,X2o@ X452吗 :反T,X经 X-A 5。一康本作简谐振动,周期T,质点由平衡位置到二分二轰天位移处所需最短时间为 ;由最大位移到二分之一最大位移处所需最短时间为T 6. 两个完全相同的单摆(m,l均同)A、B,开始时,将单摆A向左拉开一小角0。,将单摆 B趴向右拉卉 小角20。,若将它们同时从静止释放,则它们在 处遇,相遇的时间为 2。 7.将单摆从平衡位置拉开,使摆线与竖直方向成一微小角度日,然后由静止释放任其振 刻,从放手开始计时,若用余弦函数表示其运动方程,则该单摆的初位相为 () (B)o; (C) D)- 二、计算题 1.一物体沿x轴作谐振动,振幅为10.0cm,周期为2.0s。在t=0时坐标为5.0cm,且 向x轴负方向运动。 ,20
(C)Ta)Tb)Tc (D)Ta(Tb<T。 釉爪蓝N 关 ( 均 不 计 阻 力 则 它 们 的 周 期 ;由 最大位移到二分之ˉ最大位移处所需最短时间为~钅彐「~一° 全 相 同 的单 德 (m,J均 同 )A、 B,开始 时 ,将单 摆 A向 左 拉 开 一 小 角 θ0,将单 摆 不甬 2θ0,若将它们同时从静止释放,则 它们在 的时间为 平衡位置拉开 ,使摆线与竖直方向成一微小角度 θ,然后由静止释放任綦 振 计时,若用余弦函数表示其运动方程9则 该单摆的初位相为 (3) (B)o; (C)詈; 1.一物脉沿 x轴作谐振动 ,振 幅为 10.0cm,周 期为 2.0s。 x轴负芦向运动。 饣乃灬沁 孓邢 在 t〓 0时坐标为 5.0cm,且

(1)写出振动方程 (2)当物体在x=-5.0cm处向x轴负方向运动时,其振动相位(ωt+p)等于多少? (3)在上述运动状态时,物体的速度和加速度各是多少? w=2平=m =locm·CsLT6+p) C3) o心p=土,p=马,X:locmCsLTrad5·t7) =-AuSinlutto) =-342 2一质量为0.2kg的质点作简谐振动,其运动方程为x=0.6sin(5t-7)式中x以米二-0o m/s 计,t以秒计,求: 二272 (1)振动的振幅、周期; (2)振动质点的初始位置和初始速度; a三-hv郎lu6的 (3)质点在最大位移一半处且向x轴正方向运动的时刻,它所受的力、速度和加速度。 2 (1)A=o、6m (3) 二4935 T=积=2罗-65 omL (2 t-o,y=06s-5) 56-马2名) 二、0、6%m V=a6 xsx ca君 V=0、6x5×愁C马) 二 260m/3 二 0÷0.6×号=-75 3.如图两个相同的谐振子a和b,周期T=2s,将两个振子分别从平衡位置向右拉5Cm,2 然后先放开a,0.5s后再放开b,以放开b为计时起点(t=0),则两个谐振子的振动方程 x=5cm·oCTa5·6+马) F=-15/ x=o·@rads·t) 在同一坐标中,画出二条振动曲线。 N⑦a w⑦b ·21·
中乙: × (1)写 出振动方程 (2)当 物体在x=-5。 Ocm处 向x轴负方向运动时,其振动相位(ot+♀ )等 于多少? u△ 彡 罕 皙 飞笈ε;砌 体隗 度 /口 1 6^口 乙s色 π舌七♀9 珥 【 v-犰 蟹 L侈 弋甲二锷 可彻 眙 ·犭十:9c子 纪甲 3二 ~湃 JDin‘Ⅱ执⑺ =圭 '?=ξ 丿rv乙阳·乙sε =~亻乙午吁/⒉ 2.一质量为?2kg的 质点作简谐振动,其 运动方程为圣=0.6si?(5t^号 )式 中x以 米 tF°‰ 计,t以 秒计,求 : ∶` ≡ 馄 (1)振动的振幅凋 期; (2)振 动质点的初始位置和初始速度; 终 二媲 仞冶叨 (3)质点在最大位移一半处且向x轴正方向运动的时刻,它所受的力、速度和加速度。凶〃 = ˉ 乙 二 钾、 `J ‘ ° '化 ⒎ c丨 9虍 --0、 6冫 ‘b, ^ T二 = ∫、△6‘ 口、 ‘’M(厂 ;’ 一9、 ‘M u夕 `r Ξ工二 ∞ 。2' 钅¨ ' V二 次傲⒈×协号 k/=u、 ‘κf κ滠丛Gˉ △’ 二 2`彡 口¨~ ˉ 9 仇 二 ,刁 ~侈 κ C《 ζ△钅 二 -7夕 3.如 图两个相同的谐振子 a和 b,周 期 T=λ,将两个振子分别从平衡位置向右拉 5cm,“吒 · 然后先放开 a,o.5s后 再放开 b,以 放开 b为计时起点(t〓 0),则两个谐振子的振动方程 、= 5c队 ·夕、C丌 rd/s· 名) ; 气〓虫 h鱼 Lu砩 凵 L璧 L_⊥ ~° F:^′ `臼¢ 在同一坐标中,画 出二条振动曲线。 ∝ “ˉ百三弓务丿 ·21
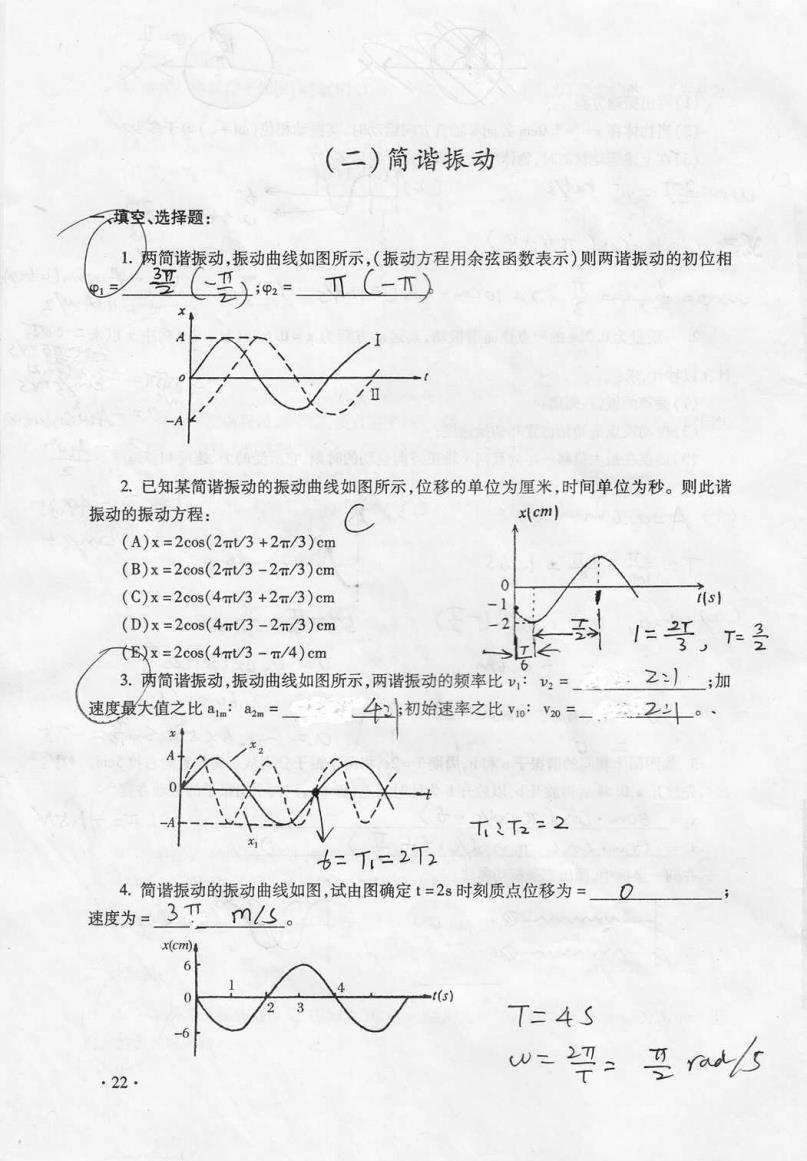
(二)简谐振动 填空、选择题: 1.两简谐振动,振动曲线如图所示,(振动方程用余弦函数表示)则两谐振动的初位相 2.已知某简谐振动的振动曲线如图所示,位移的单位为厘米,时间单位为秒。则此谐 振动的振动方程: C x(cmi) (A)x=2cos(2mt/3+2/3)cm (B)x =2cos(2mt/3-2T/3)cm (C)x =2cos(4mt/3+2/3)cm As) (D)x=2cos(4mt/3-2m/3)cm (Ex=2cos(4πt/3-π/4)cm 1=号,T2 3.两简谐振动,振动曲线如图所示,两谐振动的频率比,:=。2);加 速度最大值之比a1m:a2m 小初始速率之比vov”=一.2斗。· 七7 TT2=2 6=T1二2T2 4.简谐振动的振动曲线如图,试由图确定t=2s时刻质点位移为=Q 速度为=3Tm飞。 x(cm) T二4S 6 w= a 22·
(二 )简 谐振动 简谐振动,振动曲线如图所示,(振 动方程用余弦函数表示)则两谐振动的初位相 旷 X ^ 0 -^ 2.已知某简谐振动的振动曲线如图所示 ,位移的单位为厘米 ,时 间单位为秒。则此谐 振动的振动方程: (A)x〓 2cos(2πv3+2T/s)c叩 (B)x〓 2cos(?剥 `-2T/3)cm (C)x〓 2cos(4πt/3+2qT/3)cm (D)x〓 2cos(4πt/3-2T/3)om ο丬 一2 → 3一 冫 且B忄 一一 z x〓 2cos(4πt/3-π/4)cm 简谐振动 ,振动曲线如图所示,两谐振动的频率比 v1: 吾 V2 〓 ⒎ ;力Ⅰ 大值之比a婉 :a‰ 〓⊥ |∷ ` ` t辶 飞 ’亠 钅:TI:冫t冫 4.简谐振动的振动曲线如图,试 由图确定 t〓 2s时刻质点位移为 = , ___ˉ ; 速度为〓3T 田尔 。 |:珀 丬 ;初 始速率之比 喻 vzO=~∴4o 、 ' T= 凵 L “ 刀一T x1c’ ’) o ·22· 亠 ∶罾L形

5.佩强系数相同,质量忽略不计的弹簧与一质量为m的物体构成如图所示的四个振动 系统,务自的固有频率分别为01,02,,04,则 W1=2w w-w w;=w (A)01=0.5w2,3=04; (B)01=0.50,02=04 (C)@1=03,02=04; (D)w1=03,02<04; .一质量为m的物体挂在倔强系数为K的弹簧下,振动圆频率为0,若将此弹簧分割 成二等份。将物体挂在分割后的一根弹簧下,则振动圆频率为 (A)2w; (B)2w; (c)2 二、计算题: 1.一定滑轮的半径为R,转动惯量为J,其上挂一轻绳,绳的一端系一质量为m的物体, 另一端与月一固定的轻弹簧相连,如图所示,设弹簧的倔强系数为k,绳与滑轮间无滑动,且忽 略轴的摩擦力及空气阻力,现将物体m从平衡位置拉下一微小距离后放手,证明物体作简 谐振动,并求出其角频率。 mg-Ti=ma mt (T一T)R二. 2 个T T2=kx T:+设 二kx+登 ma+径=9-k天 .23 久之 mg-kx 迭义三 kx' mt对|2 则a二一mt灯Jl2
(D o: ω 4 (A)ω 1〓 0.5ω2,ω3〓 ω4; (B)ω 1=0.5ω3,ω 2=ω4; (C)ω1=ω3,ω2〓 ω4; (D)ω1=ω3,ω2(ω4; O.一 质量为 m的物体挂在倔强系数为 : 成二等份。将物体挂在分割后的一根弹簧下 (02ω ; (B冫尻; (⑴钅;∷ 其上挂一轻绳,绳 的一端系一质量为 m的物体, t弹簧的倔强系数为 k,绳与滑轮间无滑动,且忽 略轴豹摩擦力及空气阻力,现将物体 m从平衡位置 谐振动,并求出其角频率。 ^宋 : 叼 ^丐 强系数相同,质量忽略不计的弹簧与一质量为 m的物体构成如图所示的四个振动 自的固有频率分别为 ω1,吨 ,og,ω4,贝刂 Cπ 一0)R二 ∷Ι灸 口 kz 飞 丁 I=T冫 Γ+ 迎贮 =叼 -R9 二 妃觅 忄遐 艹 ∶ l VV≈ +2翌 R· 民 ` b R 一一 ≥灿甲一泛x 。留 史豕γ/=¨ · la。l久 二一犏

2/一质量为100g的物体,以振幅1cm作简谐振动,最大加速度为4cm·s。求: (1)振动的周期: L2)E=上mw2A2 (2)总能量; (3)通过平衡位置时的动能; (4)物体在何处,动能为其势能的一半。 o.l×45包o1网2 w=namA =rad 3)E1O)=E=2X10J T= 4) Ek2 Ep Ek+Ep=E →6,22E 4.如图所示,倔强系数为K的轻弹簧和质量为M的物体组成水平弹簧振子,振幅为A,二mw并 有一质量为m的粘土,从高为h处自由下落,正好落在物块M上,试计算下述两种情况:二三wX 1)M通过平衡位置时;(2)M为最大位移时,振动的周期,振幅和谐振动能量。 x=号A 082m (1)与(2)是同一个系统, 都是由弹簧k和质量为M+m的物体组成, M 7777777 故二者具有相同的振动周期 T-2T Mtm ()粘上为 4w=A m黏到M上,水平方向动量守恒, 黏上后共同运动的速度为 V=MUM MA k M十m-M十mA 黏上后系统的能量为E三htn)V产- 2M+%) A MkAR 黏上后系统的振幅A'满足E'=kA'2,可得剧三 2CMtm) ·24· (2)M在振幅处,速度为0。m黏在M上后不改变速度,故系统能量不变 所以5'2kA2 A-A
作简谐振动,最大加速度为4cm· s2。 求: c冫 9E冫 士h山%2 (2)总 能量; (3)通过平衡位置时的动能; (4)物体在何处,动能为其势能的一半。 C|9 久跷叹二比产∧ :兰 ˇ 。∶t勹 女莘。F·∶;忽 Di⊙ ∷ - ~r ˉ 2×r。 J 0V Ekto’二E毛以°J { 下 二 竿 △`飞 C勹 最 粪 Ep→ ℃ 膏 y 凵叫嘛 丨\=亠nv1‘ C、 9 (1)与(2)是同一个系统, 。 9 ^仁 所示,倔强系数为Κ的轻弹簧和质量为M的物体组成水平弹簧振 Ξ默 ‘膏蛊:L冒徙饣;i m的粘土,从 高为 h处 自由下落,正 好落在物块 M上,试计堡 )M通 平衡位置时;(2)M为最大位移时 ,振动的周期 ,振 幅和谐振动能量。 Ⅴ ⒎ 2π 罟 叫硐 二 J`g艹 环 戋′ 炮 氏X二 4°氵,沔 膘 ∞={÷ 内 邝〓 一一 厢 厍 ^Ι rι 丨 ◆II`` L′=茔 k沽 Σ 虍)、 。24· 都是由弹簧k和质量为M+m的物体组成, 故二者具有相同的振动周期 M m黏到M上,水平方向动量守恒, 黏上后共同运动的速度为 M 黏上后系统的能量为 黏上后系统的振幅A'满足E'=kA'/2,可得 2 M在振幅处,速度为0。m黏在M上后不改变速度,故系统能量不变 所以

(三)振动的合成 一、填空、选择题: 1.一物体同时参与同一直线上两个谐振动 x=0.05c0s(4mt+7)(S0 .03cm(m)(S) 合振动振幅为 007 2.两个同方向同频率的简谐振动,振动表达式为 3=6×10-2cos(5t+牙)(SI) x2=2×102sin(π,5)(望) 它们合振动的振幅为 4X心m ;初位相为 / 3.两个同振动方向的简谐振动振动曲线如图所示,合振动振幅A,一A! 合振动的振动方程是CAA)风心七t?头在图中画出合振动的振动曲线。 x,() 4.两个同振动方向同频率的谐振动,其合振动振幅为20cm,与第一个谐振动的位相差 Y为。若第一个谐振动的振辐为10,cm,则第二个谐振动的振幅为 10 第一、二两个谐振动的位相差是T) 5.,下列几个方程,表示质点振动为“拍”现象的是 (B) (A)y=Acos(t+)+Bcos(t+ (B)y=Acos(200t)+.Bcos(201t+) (C)x=A cosot, y=A2sin(ot+p】 (D)x=A:cosot, y2=Az cos2ot 6.两组互为垂直的谐振动为 (1) (2)X x acosot y=bsinot 其合振动 不是 谐振动(答是或不是),轨迹方程为木祁陌圆 两者区别是 ·20… 顺射,)造时新
、=6× 10ˉ 2cos(5t+子 ×⒊) 它滁癫的淼i′∵环;P卜 ;初 位才目为 π /亠 合扈的餍篷翌晏骘孓智箩曜鳜嚣 獭笤螽琪←—, 画出合振动的振动曲线。 (三 )振动的合成 一、填空、选择题: 订′ | j 1.一 物体同时参与同一直线上两个谐振动∷ \〓 0,05cos-÷ t:+于×sI) '° 丸=0,O3c乩 (4付 +瞥)(pI冫 合振动振幅为__田 、07∴ ∷∷∶ 2.两个同方向同频率的简谐振动,振动∷表达式为 4.两个同振动方向同频率的谐振动,其合振动振幅为 ⒛cm,与第一个谐振动的位相差 为詈?芦笨丁个渭振动的振幅为 10√民m,则第二个谐振动的振幅为 /D‘‰∽ 第一、主锸个谐振劫的隹 相差是 。 λ∶?Ι众尕吞T霞霆『已饣器∴严象的是 (B) (B)y=Acos(200t)+饣 Bcos(20It+【 p) (C)x=Alcooω t, y=A2⒍ n(ωt+cp) (D)x=A1qosωt, y2=A2c。 s2ωt 6,两组互为垂苴的谐振动为 ∷ ⑴〖1=茹 叽 蕊 毫 j禾勤 j迹 其合振动 ∶程疵 脏 ⊥ ∶ 两者区别是 。20 】:v⊥ΞL卩鲫

7.什么是共振? 在国其月小性外力作用下,痕福达极有 产生共振的条件是 外力顿率人固有颈峰 的视象 二、计算题: 1.两个同振动方向,同频率的谐振动,它们的方程为 x:=5cosmt(cm) x=5cos(mt+受)(cm) 如有另一个同振向同频率的谐振动x3,使得x1,x2和x三个谐振动的合振动为零。求 第三个谐振动的振动方程。 xgot+婴) ×3 2.已知两同振向同频率的简谐振动 x=0.05cos(10e+号s0 x=0.06cos(10E+写)(sl0) (1)求合成振动的振幅和初相位; (2)另有一个同振动方向的谐振动x=0.07cos(10t+φ)(sI)问中为何值时x1+为的 振幅为最大,”为何值时x2+X3的振幅为最小。 (3)用旋转矢量图示(1)、(2)的结果。 1)A=0、o89m9=b82° 飞2)P=琴时X3报幅大,P:婴时,w振幅易小 X2 3.已知两谐振动v-t曲线如图。它们是同振动方向同频率的谐振动。求 (1)两谐振动的振动方程;丁=2河,W=平=() Umax=A=15A (2)它们的合振动的振动方程。 =2 cm.s-A=2cm (cm·s- X=2cmlost+) X=X以2=25cm.6+)
7。 什 产 么 生 是 共 共 振 振 的 ? 条逆件是 燮睚婴巍邂梦纬耱 二、计算题: 1. 咖 5cο sπ t 硼蝴〓 刷 〓5c(硐 獭 个 的 蜘 v有 另.'醐 虫口 第三个 垧 ft( 向 cm 刚 程 c 叭 向 方 一 振 动 为 零 求 口 个 谐 振 动 的 、 丿 一〓 钶一午 `' x 沩 哪 }和 咕 ' 咖 和 ?石 义 程 × x2 们 πt 伽 耐 缃 协 囗 s(τ ,使 珈 5cο sΛ 吁 ·各虾≡ r 振 i “·. 渤 ≡ 蝴 x2瀚 ∷奸 频 率 ∷X 率 ,同 扌 ㈤ 獭 呈。 κ3 2。 已知两同振向同频率的简谐振动 Kl=0。 “∞s(10t+导 α虹) 九=0.“ ∞s(10t+昔 π)(sI) +、 的 (1)求 合成振动的振幅和初相位 , (2)另 有一个同振动方向的谐振动 、 〓0.凹 ∞s(10t+♀ × d)问 9为何值时 x1 振幅为最大,9为 何值时 勤+xR的振幅为最小。 (3)用 旋转矢量图示(1)、 (2)的 爹雳&、 j ‘l)虍 ˉ口、o刀 vΛ '.PE (v忤 挈 愁 圹 饣勹舀豇J瞬 '忤 亻 β甫又勰 3黝劂 排 '× 2 °喇黠藤季FF了 ^漾圭的 淳雩T⒎鸟 阳 栩 3。 已知两谐振动vˉ-t曲 线如图 。 ,己 η ⑴ 两谐振动醐 渤 方程;T|冯 四 =等 。∫时 (?)它 们的合振动的振动方程。 冖9C"‘ s'I A *i△ 三c⒒ 缸(古 十冖 ) ⑾ 丸=-· 纪o砹 〕 ×二×丨十×L=)亻豇乙h、 犰※乡{疡妥D 0彡 vtc″ °‘㈠)
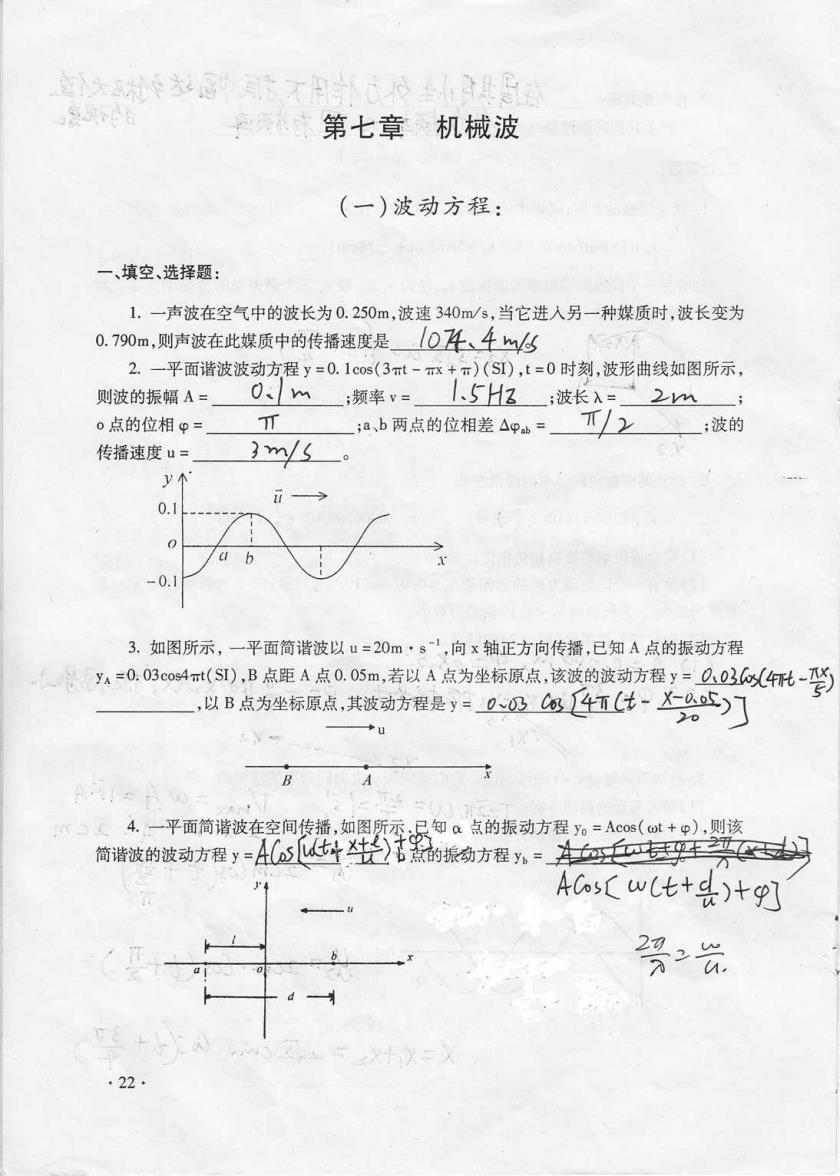
面年8的不日心代士是 第七章机械波 (一)波动方程: 一、填空、选择题 1.一声波在空气中的波长为0.250m,波速340m/s,当它进入另一种媒质时,波长变为 0.790m,则声波在此媒质中的传播速度是0(、车5 2.一平面谐波波动方程y=0.1cos(3mt-x+π)(SI),t=0时刻,波形曲线如图所示, 则波的振幅A= 0m;频率v= 、5Hz;波长λ=2m 0点的位相p= 币 ia、b两点的位相差△pb= ;波的 传播速度u= 3m/5。 y个 0.1 -0.1 3.如图所示,一平面简谐波以u=20m·s,向x轴正方向传播,已知A点的振动方程 y4=0.03co4mt(S1),B点距A点0.05m,若以A点为坐标原点,该波的波动方程y三03以4化-学 以B点为坐标原点,其被动方程是y0~及⑧4红t-%5)] U 4.一平面简谐波在空间传播,如图所示,只知a点的振动方程y6=Acos(wt+p),则该 简谐波的波动方程y=45生安》古的振绮方程,=女买妈 ACosw(比+头)+9] 号元 ·22
第七章 Ⅱ机械波 (一 )波动方程: -、 填空、选择题 : 1.一声波在空气中的波长为 0。 乃0m,波 速 “0m/s,当 它进人另一种媒质时,波 长变为 0。 7∞m9则声波在此媒质中的传播速度是 则波氙黠F逻苎ΙEF豇Ⅰ苎J谣象 ˉ依l凹l丿 =∶拶罗屮隼η o点 的位相 ♀〓 钅播速度 u〓 ___⒓ 二孕生L~。 3,如 图所示,一平面简谐波以u〓 ⒛mrs∴ ,向 x轴正方向传播,已 知A点 的振动方程 h=0:O3∞斟Tt(sT),B点 距 A点 0.Osm,若 以A点 为坐标原:点 :该波的波动方程y△互业Ⅱ玫彡萜 -∶p梦 潦点,其菠劫芳程皂 ^二 —————— ’以 B点为∷坐标` ~口 △况`鱼凵丝纟Ⅱ彡|茎△梦竽夂冫 -ˉ-ˉ十 u J ∶ 4.∶ ∷平面简谐波刁 简谐波的波动方程 y= ;a小 两点的位相差 Afpab=~下/~;波 的 46s〔 Gv‘t+去 )+q二 〓 τ阢 勿一 冫^ °22
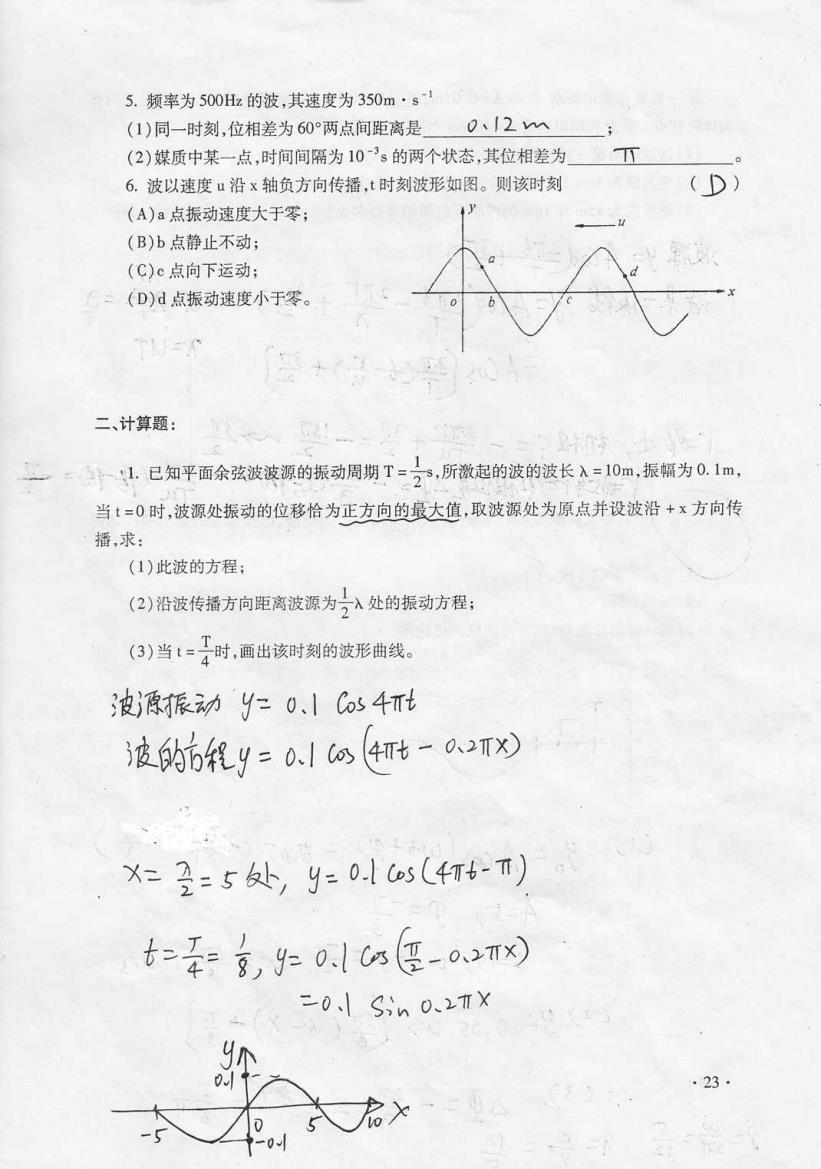
5.频率为500Hz的波,其速度为350m·s1 (1)同一时刻,位相差为60°两点间距离是 0、|2∞ (2)媒质中某一点,时间间隔为10’s的两个状态,其位相差为 6.波以速度ù沿x轴负方向传播,t时刻波形如图。则该时刻 (D) (A)a点振动速度大于零; (B)b点静止不动; (C)c点向下运动: ~(D)d点振动速度小于零。 二、计算题: 1.已知平面余弦波波源的振动周期T=,所激起的波的波长入-=10m,振幅为0.1m, 当t=0时,波源处振动的位移恰为正方向的最大值,取波源处为原点并设波沿+x方向传 播,求: (1)此波的方程; (2)沿波传播方向距离波源为入处的振动方程; (3)当1=买时,画出该时刻的波形曲线。 源振动之0、1Co54t 液6程y=0.1@4t-T) X=2=5处,9=0.s(4T6-T) =不,9=0.每-网 二0S,n02TX .23
5.频率为sO0Hz的波 ,其速度为350m· s (1)同 一时刻,位相差为60° 两点间距离是 -1 口、∫∶z~灬 (2)媒 质中某一点 ,时 间间隔为 10^3s的 两个状态 ,其位相差为 π 。 6.波 以速度 u沿 x轴负方向传播 ,t时 刻波形如图。则该时刻 (~1)) (A)a点振动速度大于零; (B)b点静止不动; (C)c点 向下运动; (D)-点 振动速度小于零。 二、计算题 : \1。 已知平面余弦滹埤洱叩振砂周却T丁 ÷s,脐 翠袒叩埤叩波长λ=10叩 ,振 幅为0,1m, 当t=0时 ,波源处振动的位移恰为正方向的蕞大值,取波源处为原点并设波沿+攵 方向传 播,求 : (1)此 波的方程; (2)沿 波传播方向距离波源为÷ λ处的振动方程; (3)当 t=÷时9画 出该时刻的波形曲线。 丿 丿 石 犭 一'∷ 丌冫 一午 古 丶 乙 ⒄告 一 π J/ 厶色 列匕黧弘劢 ·y:g、 丨6s4丁↓ 踉 觥 彳1y彡 帆丨沆 t+T+'久 9T×D x=璧 二J涉心/ g:0。 丨 y二 口:丨 乙0、 丨 亠 0、 冫π∴κ) ζ忄h° 、)π × ·23