
§3高斯定理 一.电力线 用一族空间曲线形象描述场强分布 通常把这些曲线称为电场线(electric field line)或电力线(electric line of force) 1.规定 方向:力线上每一点的切线方向; 大小:在电场中任一点,取一垂直于该点场强 方向的面积元,则通过单位面积的电力线数目, 等于该点场强的量值
§3 高斯定理 一.电力线 用一族空间曲线形象描述场强分布 通常把这些曲线称为电场线(electric field line)或电力线 (electric line of force) 1.规定 方向:力线上每一点的切线方向; 大小:在电场中任一点,取一垂直于该点场强 方向的面积元,则通过单位面积的电力线数目, 等于该点场强的量值

dΦ 匀强电场元 E ds dΦ=Eds, 若面积元不垂直电场强度, 电场强度与电力线条数、 面积元的 关系怎样? 由图可知通过ds和ds,电力线条数相同 ds dsn d中=Eds,=Eds cos e→ dφ=E·dS
E d dS = ⊥ dS ds E dS⊥ d = Eds⊥ 若面积元不垂直电场强度, 电场强度与电力线条数、面积元的 关系怎样? 由图可知 通过 ds 和 ds⊥ 电力线条数相同 d = Eds⊥ E ds = dsn ^ = Edscos d = E dS 匀强电场

2.电力线的性质 1)电力线起始于正电荷(或无穷远处), 终止于负电荷,不会在没有电荷处中断; 2)两条电场线不会相交; 3)电力线不会形成闭合曲线。 之所以具有这些基本性质, 由静电场的基本性质和场的单值性决定的。 可用静电场的基本性质方程加以证明
2.电力线的性质 1)电力线起始于正电荷(或无穷远处), 终止于负电荷,不会在没有电荷处中断; 2)两条电场线不会相交; 3)电力线不会形成闭合曲线。 之所以具有这些基本性质, 由静电场的基本性质和场的单值性决定的。 可用静电场的基本性质方程加以证明
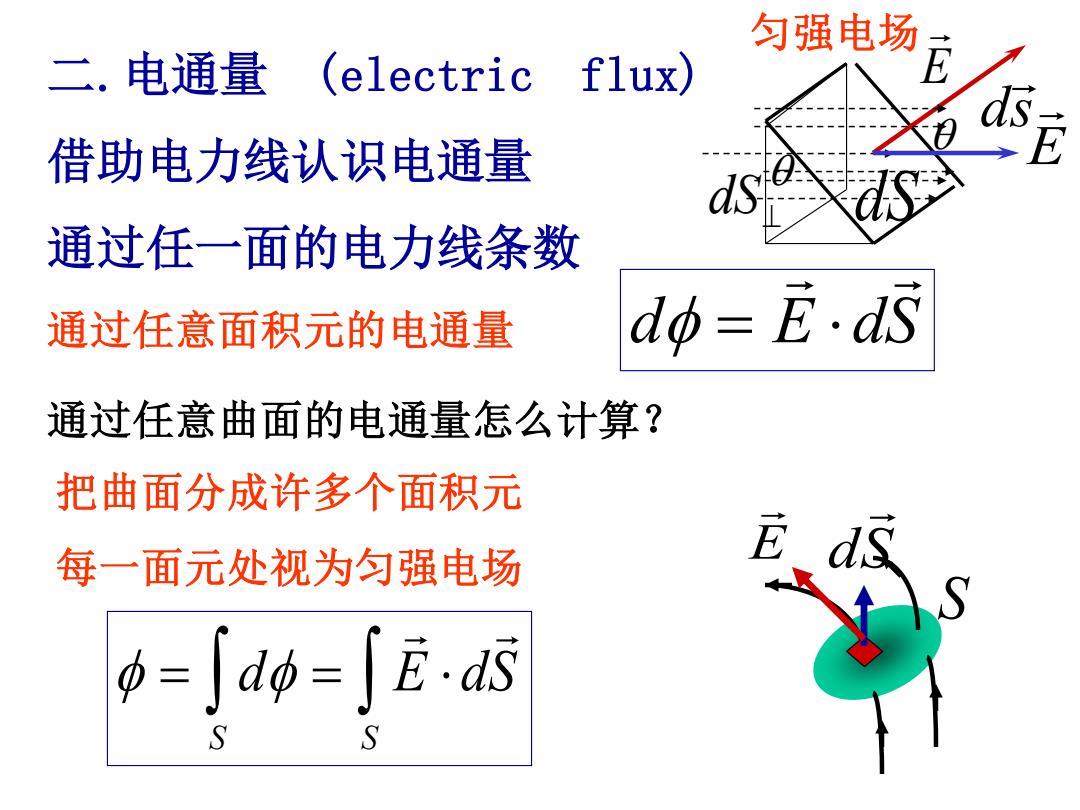
匀强电场 二.电通量(electric flux) 借助电力线认识电通量 通过任一面的电力线条数 通过任意面积元的电通量 d=E·dS 通过任意曲面的电通量怎么计算? 把曲面分成许多个面积元 每一面元处视为匀强电场 =「d0=「Ed
二.电通量 (electric flux) 借助电力线认识电通量 通过任一面的电力线条数 = = d E dS S S dS ds E dS⊥ E 匀强电场 d = E dS 通过任意面积元的电通量 通过任意曲面的电通量怎么计算? S 把曲面分成许多个面积元 每一面元处视为匀强电场 dS E
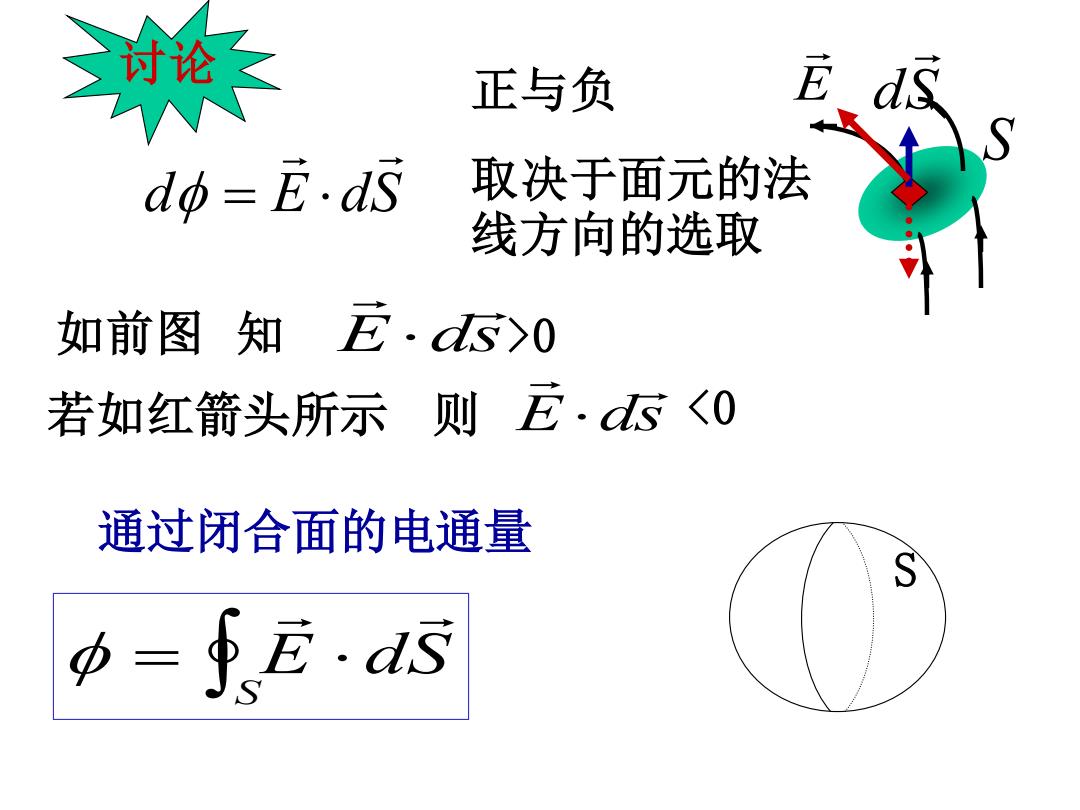
≥讨论 正与负 E dΦ=E,ds 取决于面元的法 线方向的选取 如前图知五.cd5>0 若如红箭头所示则E·d5〈0 通过闭合面的电通量
通过闭合面的电通量 = E dS S 讨论 d E dS = 正与负 取决于面元的法 线方向的选取 S dS E 如前图 知 E ds >0 若如红箭头所示 则 E ds <0 S
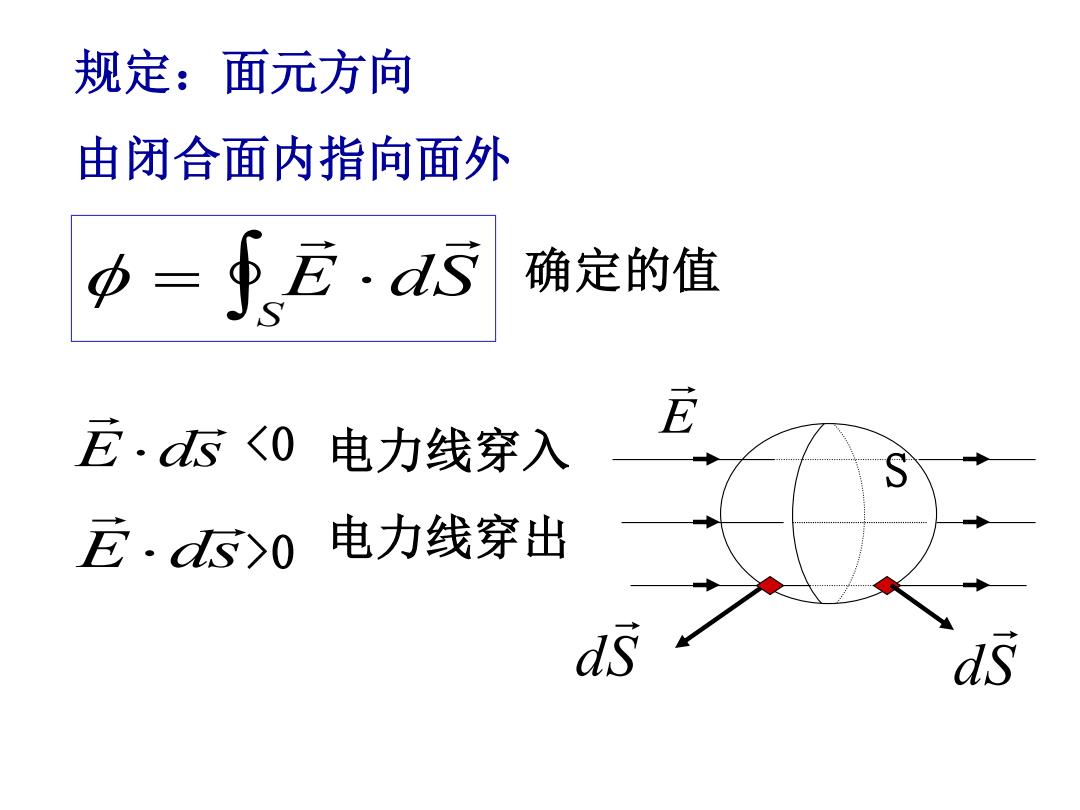
规定:面元方向 由闭合面内指向面外 确定的值 尼·d50 电力线穿出 ds ds
= E dS S 规定:面元方向 由闭合面内指向面外 确定的值 S E dS dS E ds >0 E ds <0 电力线穿入 电力线穿出

三.静电场的高斯定理 Gauss theorem 1.表述 在真空中的静电场内,任一闭合面的电通量 等于这闭合面所包围的电量的代数和除Eo。 ∮Ed
三.静电场的高斯定理 Gauss theorem 1.表述 在真空中的静电场内,任一闭合面的电通量 等于这闭合面所包围的电量的代数和 。 0 = i i S q E dS 内 0 除以
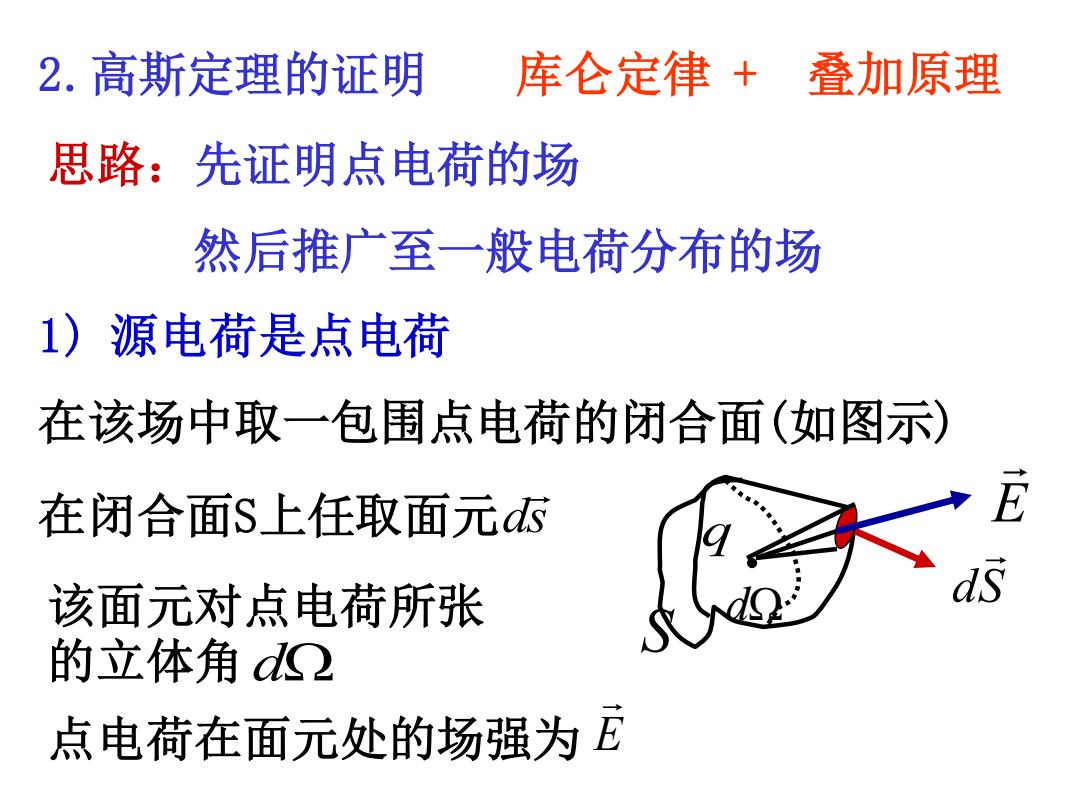
2.高斯定理的证明 库仑定律+叠加原理 思路:先证明点电荷的场 然后推广至一般电荷分布的场 1)源电荷是点电荷 在该场中取一包围点电荷的闭合面(如图示) 在闭合面S上任取面元d 该面元对点电荷所张 的立体角d① 点电荷在面元处的场强为E
库仑定律 + 叠加原理 思路:先证明点电荷的场 然后推广至一般电荷分布的场 1) 源电荷是点电荷 在该场中取一包围点电荷的闭合面(如图示) 2.高斯定理的证明 q S dS d 在闭合面S上任取面元 ds E 该面元对点电荷所张 的立体角 d 点电荷在面元处的场强为 E
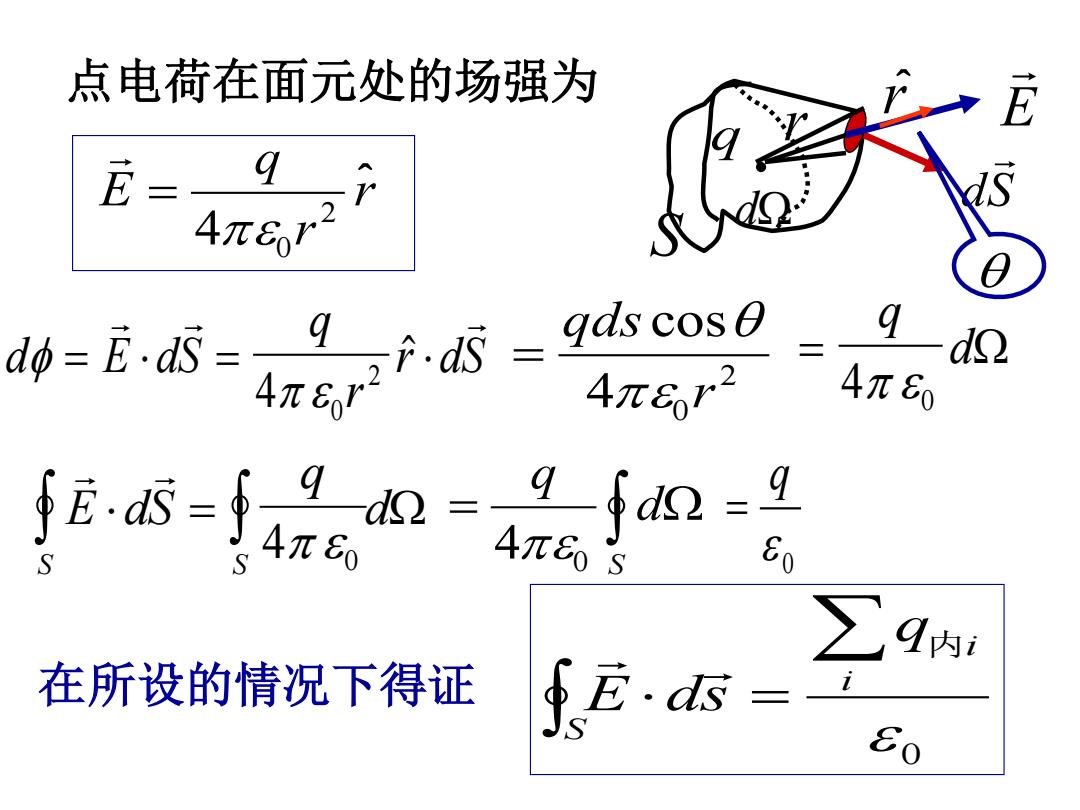
点电荷在面元处的场强为 E= 9 4π6r do=E.ds=9 f.d5 =gds cose -d 4元8r 4π6r2 4π60 fEs=f,92=9fu0=9 4π83 0 ∑9: 在所设的情况下得证 E.ds Eo
d E dS q r r dS = = 4 0 2 = q d 4 0 E dS q d S S = 4 0 0 = i i S q E ds 内 q S dS d E 点电荷在面元处的场强为 r r q E 2 4 0 = ^ r r ^ 2 4 0 cos r qds = = S d q 4 0 0 q = 在所设的情况下得证

2)源电荷仍是点电荷 取一闭合面不包围点电荷(如图示) ds, 在闭合面上任取面元dS,q 该面元对点电荷张的 d 立体角d2 也对应面元dS, 两面元处对应的点电荷的电场强度分别为尼,, d=+6,= + 4π6 4π8r2 gds,cose-qds,cose, =0 4π6 4π62
2)源电荷仍是点电荷 取一闭合面不包围点电荷(如图示) dS1 S d E1 1 r ^ 在闭合面上任取面元 dS1 q d 该面元对点电荷张的 立体角 dS2 也对应面元 2 dS 两面元处对应的点电荷的电场强度分别为 E1 E2 , 2 r 1 r E2 1 1 2 2 d E ds E ds = + 2 2 2 0 2 2 1 1 0 1 4 4 r ds r q r ds r q = + ^ ^ 2 0 2 2 2 2 0 1 1 1 4 cos 4 cos r qds r qds − = + = 0 1