
第1节黑体辐射 普朗克假设 一、热辐射 任何物体在任何温度下,都在不断地向周围辐射各种波长的 电磁波,这种由温度所决定的辐射称为热辐射 温度较低,辐射的能量较少,辐射能主要分布在长波范围 T个,辐射的能量个,短波部分的能量所占比例个 T800K T个 铁块 暗 暗红赤红黄白蓝白 辐射能量-吸收能量,T恒定,热平衡状态,平衡热辐射 热平衡状态下,辐射本领大的物体吸收本领也大:基尔霍夫定律 二、两个概念 1、单位时间内,从物体单位表面上,所辐射的波长在 入~1+d之间的辐射能dE(2,T)与波长间隔d之比 单色辐(射)出(射)度:c(2,T)=dE(, d入 SI:Js-m3 e(2,T)与、T、材料、表面状况有关 2、单位时间内,从物体单位表面上所辐射的电磁波的 总能量:辐(射)出(射)度 ET)=∫dE(,T)=ea,Tan SI:Js-m 三、绝对黑体 能够把照射到它上面的电磁波全部吸收, 没有任何的反射和透射 注意与黑色物体的区别 e(2,T)仅与元、T有关 四、黑体辐射实验规律 1、辐射曲线 e(2,T)1 特征(1)1→0,2→0 e(λ,T)→0 入m:峰值波长 e(A.TYi=E(T) (2)T个,e(2,T)个,E(T)个,n↓ 2、斯特芬-玻耳兹曼定律 E(T)=σT4,g=5.67×10-8Wm2K4:斯特芬-玻耳兹曼恒量 辐射高温计 3、维恩位移定律:T2n=b,b=2.897×103mK 1
1 第 1 节 黑体辐射 普朗克假设 一、热辐射 任何物体在任何温度下,都在不断地向周围辐射各种波长的 电磁波,这种由温度所决定的辐射称为热辐射 温度较低,辐射的能量较少,辐射能主要分布在长波范围 T ,辐射的能量 ,短波部分的能量所占比例 T 800K T 800K T 铁块 暗 暗红 赤红 黄 白 蓝白 辐射能量=吸收能量,T 恒定,热平衡状态,平衡热辐射 热平衡状态下,辐射本领大的物体吸收本领也大:基尔霍夫定律 二、两个概念 1、单位时间内,从物体单位表面上,所辐射的波长在 ~ d 之间的辐射能dE(,T)与波长间隔d 之比 单色辐(射)出(射)度: d dE T e T ( , ) ( , ) SI: 1 3 Js m e(,T) 与 、T 、材料、表面状况有关 2、单位时间内,从物体单位表面上所辐射的电磁波的 总能量:辐(射)出(射)度 E T dE T e T d SI: 0 ( ) ( , ) ( , ) 1 2 Js m 三、绝对黑体 能够把照射到它上面的电磁波全部吸收, 没有任何的反射和透射 注意与黑色物体的区别 e0 (,T) 仅与 、T 有关 四、黑体辐射实验规律 1、辐射曲线 ( , ) e0 T 特征(1) 0, T1 T2 T3 ( , ) e0 T 0 m :峰值波长 ( , ) ( ) 0 e0 T d E T m (2)T ,e0 (,T) , E(T) , m 2、斯特芬-玻耳兹曼定律 E(T) T 4 , 5.67 10 8Wm 2K 4 :斯特芬-玻耳兹曼恒量 辐射高温计 3、维恩位移定律:T m b ,b mK 3 2.897 10

e(a,T)=f(,T), eo(2,T)1 1896,维恩公式 瑞利金斯 eo(A,T)=ce-lAT 1900初,瑞利-金斯公式 eo(A,T)=c'T 维恩 2→0,e(2,T)→∞ 紫外灾难 190未,普朗克公式:e,(a,)=2c ehel akT1 h=6.63×10-345:普朗克常数 五、普朗克假设 辐射物体中存在大量的带电线性谐振子,由于带电的原因,这些 线性谐振子可以与周围的电磁场交换能量,与经典线性谐振子不 同,这些带电线性谐振子的状态和能量不能连续变化,频率为¥ 的谐振子其能量只能取hv,2hv,…,nhy,…,只能取hv的整数 倍,谐振子和周围电磁场交换能量时也只能以hy的整数倍进行 £=hv:能量子 第2节光电效应 (爱因斯坦)光量子理论 金属及其化合物在光的照射下发射电子的现象:光电效应 一、实验规律 1、实验装置 2、伏安特性 (1)u个,i个 (2)i→is: 饱和光电流 (3)=0,i≠0 (4)un:遏止电压 1 eu。=、m 1 m:光电子的最大初动能 2
2 ( , ) = , e0 T f (,T) ( , ) e0 T 1896,维恩公式 瑞利-金斯 e0 (,T) = c T c e 5 / 1 2 1900 初,瑞利-金斯公式 e0 (,T) =c3 4T 维恩 0, ( , ) e0 T 紫外灾难 1900 末,普朗克公式:e0 (,T) = 1 2 / 2 5 hc kT e hc h 6.6310 34 Js:普朗克常数 五、普朗克假设 辐射物体中存在大量的带电线性谐振子,由于带电的原因,这些 线性谐振子可以与周围的电磁场交换能量,与经典线性谐振子不 同,这些带电线性谐振子的状态和能量不能连续变化,频率为 的谐振子其能量只能取h ,2h ,,nh ,,只能取h 的整数 倍,谐振子和周围电磁场交换能量时也只能以h 的整数倍进行 h :能量子 第 2 节 光电效应 (爱因斯坦)光量子理论 金属及其化合物在光的照射下发射电子的现象:光电效应 一、实验规律 1、实验装置 m S A K R K 2、伏安特性 (1)u ,i i (2) :饱和光电流 S i i S i (3)u 0,i 0 (4)ua :遏止电压 2 2 1 a m m eu v a u O u 2 :光电子的最大初动能 2 1 m mv G V

3、四个实验规律 (1)v一定,isc1 (2)廿金属,3截止频率y。(红限频率) v≥y。,可以产生光电效应 c/y。=,:红限波长 1≤,可以产生光电效应 不同的金属,截止频率不同 (3)4,或mv与v成线性关系 与光强无关 un=K(v-Vo),V≥Vo 斜率K:与金属材料无关的恒量 Vo (4)y≥y。,光电子即时发射,△1≤10-9s,与光强无关 二、经典解释与困难 光是电磁波,IcE2,光的能量连续分布在电磁场中 电子在周期性外电场作用下作受迫振动 光强越大,电子振幅越大,获得能量越大,初动能越大 只要光强足够强,用任何频率的光照射金属都应能产生光电效应 光强越弱,发射电子滞后的时间越长 三、爱因斯坦的光量子理论光电效应方程 光是一粒一粒的以光速c运动的粒子流,光量子(光子) 一个光子的能量:e=hv 光强:I=Nhv,N:光子流密度 光子流密度N与光子数密度n的区别,N=nc 光强(光的能流密度)I与光的能量密度w的区别 I=wc,w=nhv,I=wc=nhv.c=Nhv hv=A+m :一光电效应方程 A:逸出功 22=hv-A≥0,r≥ 方=%,A=h ew,=hv-A,么=v-A,么=K:恒量 e e 电子一次吸收一个光子,即时发射 I=Nhv,v不变,I个,N个,is个,is ocNocI K u。=K(w-Vo) h=eK A/e=:逸出电势,注意与AK之间电压及遏止电压的区别 3
3 3、四个实验规律 (1) 一定,i I S (2) 金属,截止频率 0 (红限频率) 0 ,可以产生光电效应 c / 0 0 :红限波长 0 ,可以产生光电效应 不同的金属,截止频率不同 (3) 或 与 成线性关系 a u 2 2 1 m mv a u 与光强无关 K ua K( 0 ) , 0 斜率 K :与金属材料无关的恒量 0 (4) 0 ,光电子即时发射,t 10 9 s ,与光强无关 二、经典解释与困难 光是电磁波, I E 2 ,光的能量连续分布在电磁场中 电子在周期性外电场作用下作受迫振动 光强越大,电子振幅越大,获得能量越大,初动能越大 只要光强足够强,用任何频率的光照射金属都应能产生光电效应 光强越弱,发射电子滞后的时间越长 三、爱因斯坦的光量子理论 光电效应方程 光是一粒一粒的以光速c 运动的粒子流,光量子(光子) 一个光子的能量: h 光强: I Nh , N :光子流密度 光子流密度 N 与光子数密度n 的区别, N nc 光强(光的能流密度) I 与光的能量密度 w的区别 I wc , w nh , I wc nh c Nh 2 光电效应方程 2 1 m m h A v A:逸出功 0, , 2 1 2 mvm h A 0 h A A h 0 eua h A , , :恒量 e A e h ua K e h 电子一次吸收一个光子,即时发射 I Nh , 不变, I , N ,iS ,i N I S a u K ( ) ua K 0 h eK A/ e u0 :逸出电势,注意与 AK 之间电压及遏止电压的区别 0
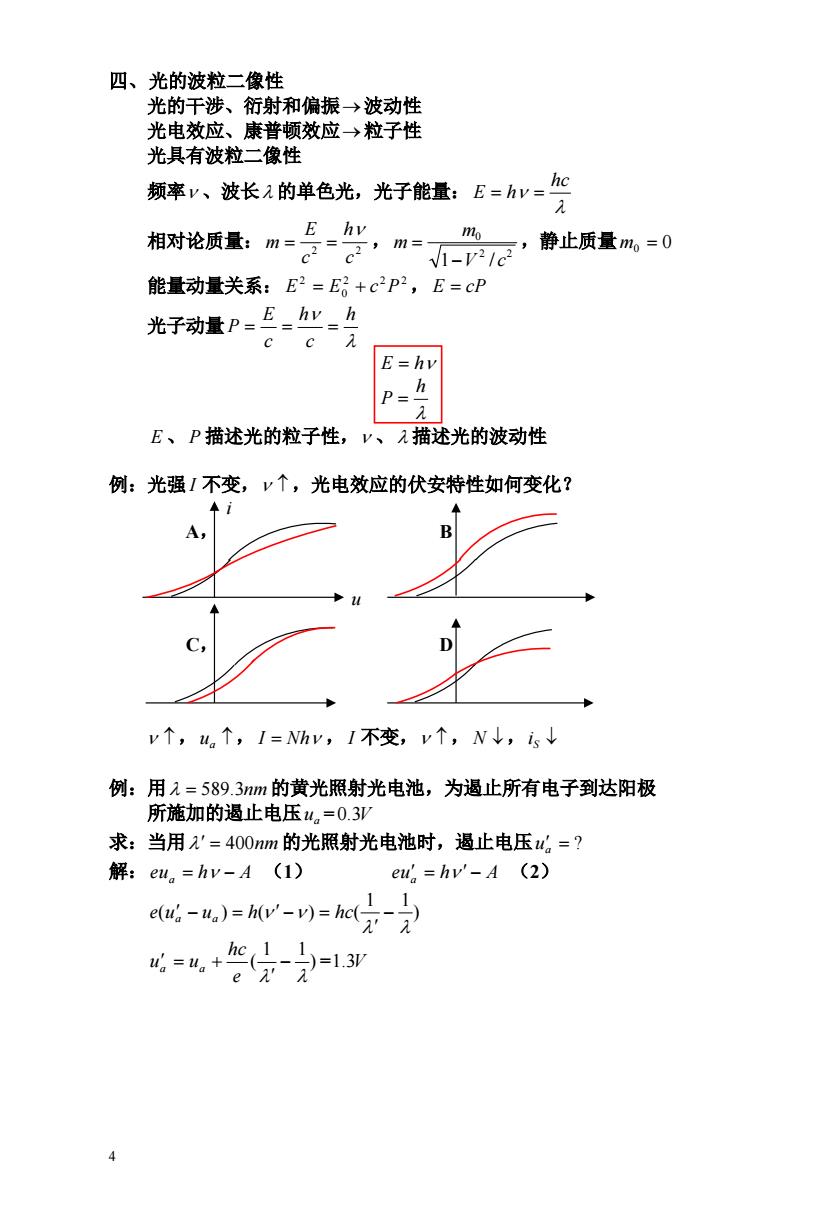
四、光的波粒二像性 光的干涉、衍射和偏振→波动性 光电效应、康普顿效应→粒子性 光具有波粒二像性 频率v、波长入的单色光,光子能量:E=hv=hC 相对论质量:m=£_hy, -rc,静止质量m,=0 mo 2’m= 能量动量关系:E2=E+c2p2,E=cP 光子动量P=E-hy=h c cλ E=hv h P E、P描述光的粒子性,y、2描述光的波动性 例:光强I不变,y个,光电效应的伏安特性如何变化? v个,u↑,I=Nhv,I不变,v个,N↓,is↓ 例:用2=589.3nm的黄光照射光电池,为遏止所有电子到达阳极 所施加的遏止电压u。=0.3亚 求:当用入'=400nm的光照射光电池时,遏止电压。=? 解:eu。=hv-A(1) eu=hv'-A (2) e-,)=w-W=hc(牙之》 4=4,+c(J -二)=1.3/ e' 4
4 四、光的波粒二像性 光的干涉、衍射和偏振波动性 光电效应、康普顿效应粒子性 光具有波粒二像性 频率 、波长 的单色光,光子能量: hc E h 相对论质量: 2 2 , ,静止质量 c h c E m 2 2 0 1 V / c m m m0 0 能量动量关系: E 2 E0 2 c 2P 2 , E cP 光子动量 h c h c E P E h h P E 、 P 描述光的粒子性, 、 描述光的波动性 例:光强 I 不变, ,光电效应的伏安特性如何变化? i A, B u C, D ,ua , I Nh , I 不变, , N ,iS 例:用 589.3nm 的黄光照射光电池,为遏止所有电子到达阳极 所施加的遏止电压ua =0.3V 求:当用 400nm 的光照射光电池时,遏止电压 ? ua 解:eua h A (1) eua h A (2) ) 1 1 ( ) ( ) ( e u u h hc a a ) = 1 1 ( e hc ua ua 1.3V

例:共轴系统,片=0.6cm r=1cm,1=20cm 石英壳 2 1a=5400A,1A,=2960A Na棒 用1=3000A照射 半透铝膜 求:平衡后,系统带电量Q=? 元=3000A 解:<入<a,Na棒产生光电效应,铝膜不产生光电效应 11) eu,=mhv-4-hv-hvshc _c-1) =Cu 2ms.hc(-↓)=4.0x10-"C
5 例:共轴系统,r1 0.6cm r 1cm , 石英壳 2 l 20cm 2r , 棒 Na 5400A Al 2960A Na 1r 用 照射 半透铝膜 3000A 求:平衡后,系统带电量Q ? 3000A 解: Al Na , Na 棒产生光电效应,铝膜不产生光电效应 = = 2 2 1 a m m eu v h A h h Na ) 1 1 ( Na hc ) 1 1 ( Na a e hc u Q Cua = ) = 1 1 ( ln 2 1 2 0 Na e hc r r l C 11 4.0 10 O