光学 第1节光源、光的单色性和相干性 一、光是电磁波 变化电磁场的传播,可用E、H描述,E:光矢量 E=E。coslo(t-)+p] E o=2πv:圆频率 V:频率 c=v:光速,1:波长 E的振动方向⊥c,横波,光强(能流密度)1cE的 可见光波长:4000-7600A 二、光源 发光的物体称为光源,发光机理: E2 E,△1≈109~10-8s,波列 E 原子激发过程 辐射过程 ☆M 按激发方式: 热光源:利用热能激发的光源 冷光源:利用电能、光能或化学能激发的光源 按辐射方式: 普通光源:以自发辐射为主 激光光源:以受激辐射为主 普通光源的发光特性:(1)间歌性(2)独立性 三、光的单色性 包含多种频率的光:复色光 具有单一频率的光:单色光,准单色光,△y或△2:谱线宽度 =及,AM,6.个,严格单色光A20,0n→n 获得单色光的方法: (1)棱镜色散(2)滤光片(3)单色光源(4)激光 四、光的相干条件 两列电磁波或光波在空间相遇 合场强E=E,+E, E2=E2+E3+2E,·E) 1=11+12+2E,·E 2E,·E2:干涉项 E=Eo cos[o,(t)+],E2 =Ezo costo2 ()+2] 1
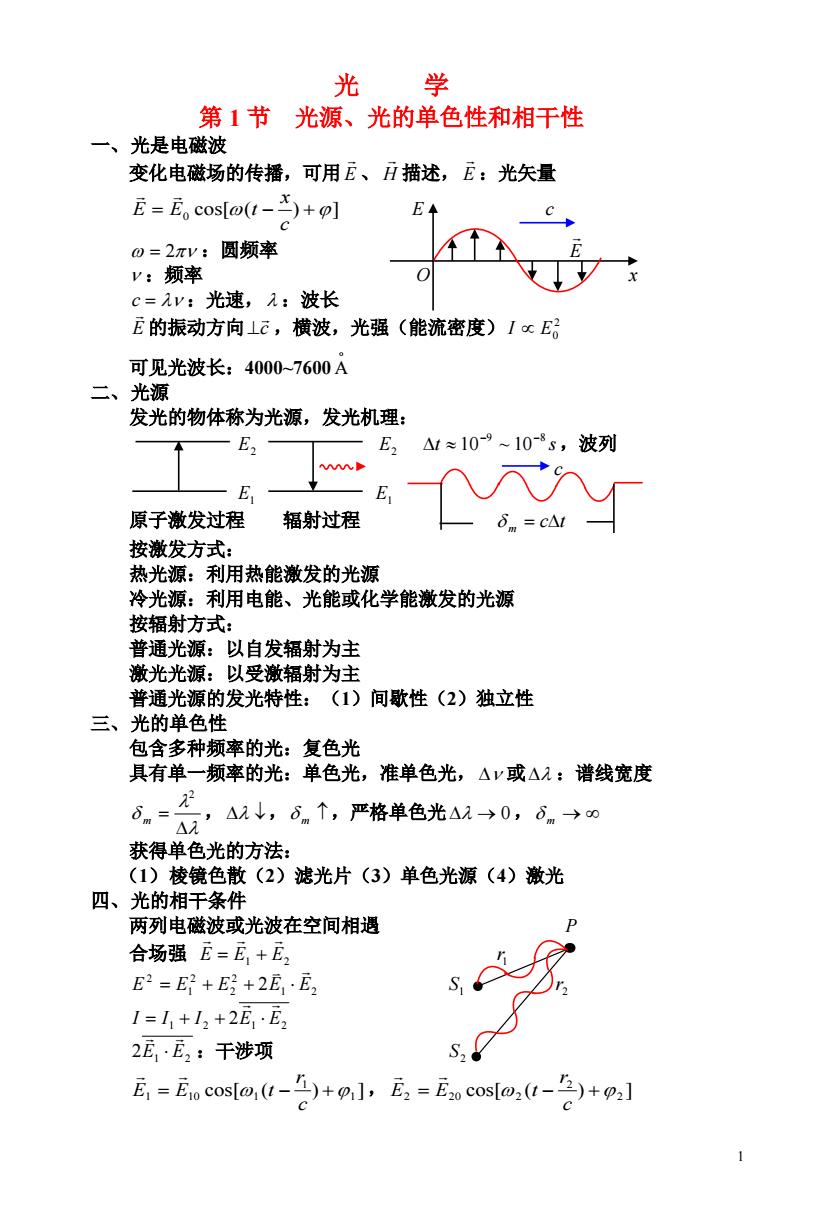
1 光 学 第 1 节 光源、光的单色性和相干性 一、光是电磁波 变化电磁场的传播,可用 E 、 描述, :光矢量 H E cos[ ( ) ] 0 c x E E t E c 2 :圆频率 E :频率 O x c :光速, :波长 E 的振动方向 ,横波,光强(能流密度) c 2 E0 I 可见光波长:4000~7600 A 二、光源 发光的物体称为光源,发光机理: E2 E2 t 10 9 ~ 10 8 s,波列 c E1 E1 原子激发过程 辐射过程 c t m 按激发方式: 热光源:利用热能激发的光源 冷光源:利用电能、光能或化学能激发的光源 按辐射方式: 普通光源:以自发辐射为主 激光光源:以受激辐射为主 普通光源的发光特性:(1)间歇性(2)独立性 三、光的单色性 包含多种频率的光:复色光 具有单一频率的光:单色光,准单色光, 或 :谱线宽度 , , ,严格单色光 , 2 m m 0 m 获得单色光的方法: (1)棱镜色散(2)滤光片(3)单色光源(4)激光 四、光的相干条件 两列电磁波或光波在空间相遇 P 合场强 E E1 E2 1r 1 2 2 2 2 1 2 E E E 2E E S1 2r 1 2 2E1 E2 I I I :干涉项 2E1 E2 S2 1 10 cos[1 ( 1 ) 1 ], c r E E t cos[ ( ) ] 2 2 2 20 2 c r E E t

下列三个条件中的任何一个出现时,干涉项2E,·E2=0 (1)E⊥E2(2)01≠02 (3)0,=02,p2-0,=f():时间的随机函数 合光强1=1+1, 非相干迭加 同振向、同频率、位相差恒定的两列光波的迭加: 合光强1=11+12+2V1,2cos△0 2π △0=0:-0-元6-) 6=乃-片:光程差 △0=±2kπ,k=0,1,2…, 1=11+12+2V112,于涉加强 △p=±(2k+1)m,k=0,1,2,1=1+12-2VI2,干涉相消 9=02,4p=-2π (2-5) 6=5-5=±k,k=0,1,2… 干涉加强 6=5-片=(2k+1)5,k=0,1,2… 干涉相消 相干迭加 光的相干条件:同振向、同颜率、位相差恒定 注:不管是相干迭加还是非相干迭加,都满足场强迭加原理 第2节杨氏双缝干涉 一、 普通光源与机械波源的区别 两个同振向、同频率持续振动 (1)振向可能不同 的机械波源的初相p、p2, (2)频率可能不同 p2-p1 (3) 初相p1、p2,2-01 2π 2π 及△0=0,-9-元-) 及△0=p2-9,- (2-r) 是恒定的,满足相干条件 不是恒定的,不满足相干条件 结论:不同光源发出的光、同一光源的不同部分发出的光、 同一光源的同一部分先后发出的光波列是不相干的 只有把同一个波列分割为两个波列让这两个波列在空间相遇 才能获得相干光 分割波列的方法(1)分波面法(2)分振幅法 杨氏双缝干涉是分波面法
2 下列三个条件中的任何一个出现时,干涉项2E1 E2 =0 (1) E1 E2 (2) 1 2 (3)1 2 , 2 1 f (t) :时间的随机函数 合光强 I I 1 I 2 非相干迭加 同振向、同频率、位相差恒定的两列光波的迭加: 合光强 I I 1 I 2 2 I 1I 2 cos ( ) 2 2 1 2 1 r r r2 r1 :光程差 2k ,k 0,1,2, I I 1 I 2 2 I 1I 2 ,干涉加强 (2k 1) ,k 0,1,2, I I 1 I 2 2 I 1I 2 ,干涉相消 1 2 , ( ) 2 2 1 r r r2 r1 k ,k 0,1,2 干涉加强 , 干涉相消 2 (2 1) 2 1 r r k k 0,1,2 相干迭加 光的相干条件:同振向、同频率、位相差恒定 注:不管是相干迭加还是非相干迭加,都满足场强迭加原理 第 2 节 杨氏双缝干涉 一、普通光源与机械波源的区别 P P S1 S1 S2 S2 两个同振向、同频率持续振动 (1)振向可能不同 的机械波源的初相1 、 2 , (2)频率可能不同 2 1 (3)初相1 、 2 , 2 1 及 ( ) 及 2 2 1 2 1 r r ( ) 2 2 1 2 1 r r 是恒定的,满足相干条件 不是恒定的,不满足相干条件 结论:不同光源发出的光、同一光源的不同部分发出的光、 同一光源的同一部分先后发出的光波列是不相干的 只有把同一个波列分割为两个波列让这两个波列在空间相遇 才能获得相干光 分割波列的方法(1)分波面法(2)分振幅法 杨氏双缝干涉是分波面法
二、杨氏双缝干涉 S,S2处p1=p2 相干光 相干光源 2π Ap=0:-0-元-)=- △p=- 2π6=2kπ 6=5-片=±k,k=0,1,2…,明纹 d △0=-2”6=2k+1z z2 S 0=5-1=2k+0吃,k=012,暗纹 =D2+x-=D2+x-d+ (1) 4 后=n++=0+r+a+号 (2) -2=(52-53+5)=2xd 设d<D,x<D,片+h≈2D,6=5-听=Dx d 6=r2-1=D x=±, 明纹中心坐标x= ,k=0,1,2… d d 0=5=)x=(2k+0,暗纹中心坐标x=(2k+) d k=0,12…,k:干涉级 k 条纹分布 第0级明纹:中央明纹 2D1/d2 注意第几级与第几条的区别 13D元/2d 讨论: DAld 1 1、相邻两明纹 0 DA/2d- 或暗纹中心间距 0 0 △x=D/d 0-D/2d 条纹均匀分布 -D/d-1 增加△x的方法 -1-3D/2d D个、d↓、个 -2D/d-2 3
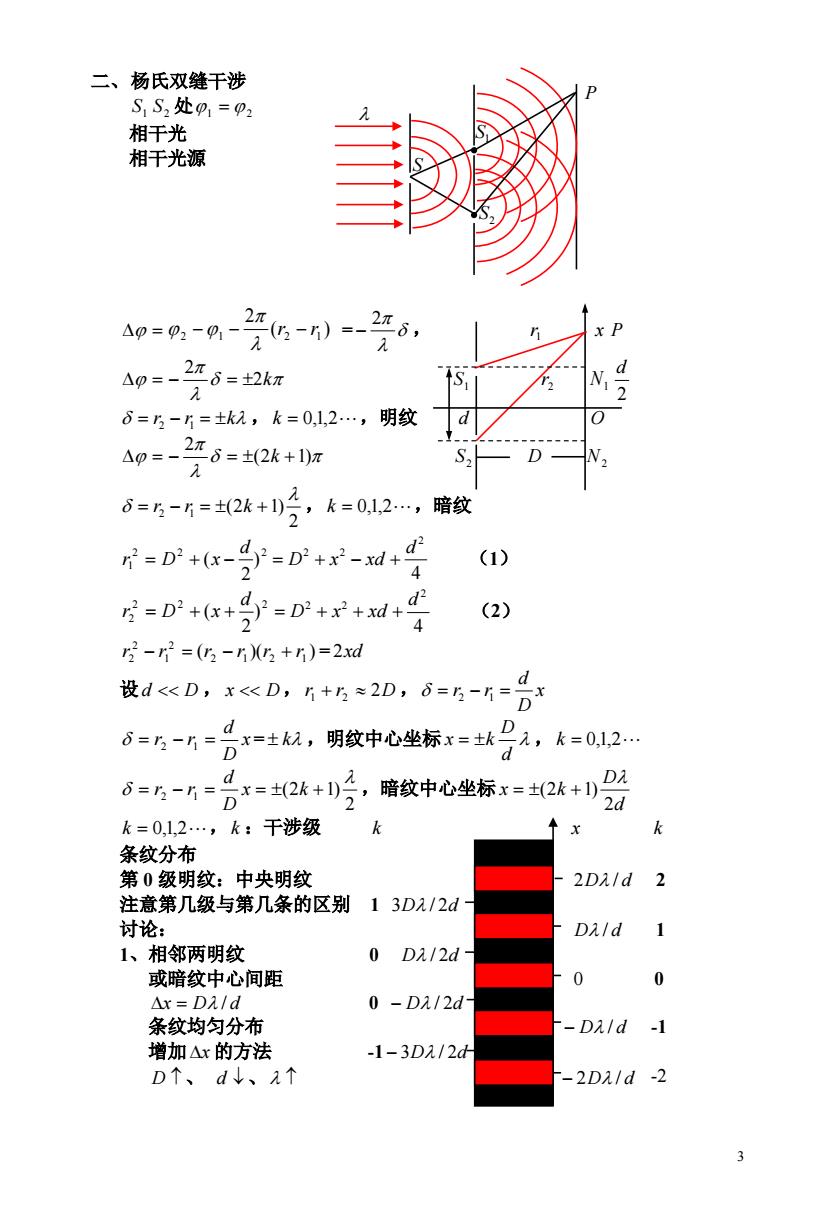
3 二、杨氏双缝干涉 S1 S2 处1 2 相干光 相干光源 ( ) = , 2 2 1 2 1 r r 2 1r x P 2k 2 S1 2r N1 2 d r r k , ,明纹 2 1 k 0,1,2 d O (2 1) 2 k S2 D N2 , ,暗纹 2 (2 1) 2 1 r r k k 0,1,2 1 2 2 ) 2 (1) 2 ( d r D x 4 2 2 2 d D x xd 2 2 2 ) 2 (2) 2 ( d r D x 4 2 2 2 d D x xd ( 2 1 )( 2 1 ) = 2 1 2 2r r r r r r 2xd 设d D , x D,r1 r2 2D , x D d r2 r1 x = ,明纹中心坐标 , D d r2 r1 k d D x k k 0,1,2 ,暗纹中心坐标 2 (2 1) 2 1 x k D d r r d D x k 2 (2 1) k 0,1,2,k :干涉级 k x k 条纹分布 第 0 级明纹:中央明纹 2D / d 2 注意第几级与第几条的区别 1 3D / 2d 讨论: D / d 1 1、相邻两明纹 0 D / 2d 或暗纹中心间距 0 0 x D / d 0 D / 2d 条纹均匀分布 D / d -1 增加x 的方法 -1 3D / 2d D 、 d 、 2D / d -2 2 S S1 S P

2、小孔S在垂直板面的方向上 移动,条纹如何变化? 在垂直板面的方向上放两个 小孔,条纹如何变化? 小孔S可变成一条垂直板面的狭缝 小孔S,S,可变成两条垂直板面的 狭缝 一双缝干涉 小孔S向下移动,条纹如何变化? 6=r2+”4-(G+乃) 6=±k入,k=0,1,2.千涉加强 6=2k+1)2,k=0,12干涉相消 3、1不同,△x不同,用日光,呈彩色条纹 中央亮纹仍是白色 从中央到两侧按由紫到红的顺序排列 设k级红色条纹和(k+1)级紫色条纹重叠 x红=k2=X=(k+D2 D d d k= 紫 4000 =1.1 入红-入紫 7600-4000 只能看到±1级彩色条纹 三、洛埃镜 当光由光疏媒质射向光密媒质 而反射时也存在半波损失现象 ±k2 k=0,1,2.明纹 6=5-+2=±(2k+D k=0,12…暗纹S 例:用1=0.5893m的钠光灯做双缝干涉实验 屏与双缝的距离D=500mm 求:(1)d=1.2mm和d=10mm时,相邻两明纹间距 (2)若相邻两明纹的最小分辨距离为0.065mm,d最大是多大? 解:( (1)Ax= d 1=12mm,4r-00x05893x10-025mm 500×10-3 d=10mm,ar-00x05893x10-03nm 2)d=R1=008300x05893x10=4.5mm 1m=103mm=10m=10°m=1010A 4
4 2、小孔 S 在垂直板面的方向上 移动,条纹如何变化? S1 在垂直板面的方向上放两个 S 小孔,条纹如何变化? S2 小孔 S 可变成一条垂直板面的狭缝 小孔 S1 , S2 可变成两条垂直板面的 狭缝 双缝干涉 3r 小孔 S 向下移动,条纹如何变化? S1 ( ) 2 4 1 3 r r r r 1r 4r O k ,k 0,1,2干涉加强 S 2r , 干涉相消 2 (2 1) k k 0,1,2 3、 不同,x 不同,用日光,呈彩色条纹 中央亮纹仍是白色 从中央到两侧按由紫到红的顺序排列 设k 级红色条纹和(k 1) 级紫色条纹重叠 红 红 紫 ( ) 紫 d D x k d D x k 1 1.1 7600 4000 4000 红 紫 紫 k 只能看到1级彩色条纹 三、洛埃镜 1r 当光由光疏媒质射向光密媒质 S 而反射时也存在半波损失现象 K 2r L ( ) 暗纹 明纹 0,1,2 2 2 1 0,1,2 2 2 1 k k k k r r S 例:用 0.5893m的钠光灯做双缝干涉实验 屏与双缝的距离 D 500mm 求:(1)d 1.2mm 和d 10mm 时,相邻两明纹间距 (2)若相邻两明纹的最小分辨距离为0.065mm ,d 最大是多大? 解:(1) d D x d 1.2mm , x 0.5893 10 0.25mm 1.2 10 500 10 6 3 3 d 10mm , x 0.5893 10 0.03mm 10 10 500 10 6 3 3 (2) mm x D d 0.5893 10 4.5 0.065 10 500 10 6 3 3 A 3 6 9 10 1m 10 mm 10 m 10 nm 10 2 S

第3节光程和光程差 双缝干涉 0,=92,△0=-5(2-1) 2=c/y:光在真空中的波长 片,5:几何路程 双缝和屏之间充满某种均匀透明介质n 介质中的光速V=c/n 介质中光的波长'=VIv=C=元/n nv 2π 5-) 5-)=-2 =-2m (nr2 -nr), nA' 定义:光程△=m △=n5+n25+…=∑n,,真空中:△=r 光程差6=△2-△1 位相差Ap=-2”d 在相同时间内,若光在介质中走过的几何路程为 则光在真空中走过的几何路程为r 光在介质中走过r的路程产生的位相变化 =光在真空中走过r的路程产生的位相变化 光程:光在介质中走过的路程折合成光在真空中走过的路程 采用光程的概念后,光的波长必须采用光在真空中的波长 例:双缝干涉 在光路2上放一厚度 为t折射率为n的玻璃片 6=5-t+nt-i n =3-5+(n-1)t -红8-2-n+n 入:光在真空中的波长 透镜的光程 透镜只改变光的传播方向,而不引起附加光程差 5
5 第 3 节 光程和光程差 双缝干涉 , 1 2 ( ) 2 2 1 r r 1r P c / :光在真空中的波长 S1 2r , :几何路程 1r 2r 双缝和屏之间充满某种均匀透明介质n n 介质中的光速V c / n 介质中光的波长 n n c V / / ( ) 2 2 1 r r 1r 2r 3r = , ( ) 2 2 1 r r n n ( ) 2 2 1 nr nr n1 2 n n3 定义:光程 nr n1r1 n2 r2 niri ,真空中: r 光程差 2 1 位相差 2 在相同时间内,若光在介质中走过的几何路程为r 则光在真空中走过的几何路程为nr 光在介质中走过r 的路程产生的位相变化 =光在真空中走过nr 的路程产生的位相变化 光程:光在介质中走过的路程折合成光在真空中走过的路程 采用光程的概念后,光的波长必须采用光在真空中的波长 例:双缝干涉 1r P 在光路 2 上放一厚度 S1 为t 折射率为n 的玻璃片 2r r r n t r t nt r ( 1) 2 1 2 1 S2 t n = 2 [ ( 1) ] 2 2 1 r r n t :光在真空中的波长 透镜的光程 A A F B F B C C 透镜只改变光的传播方向,而不引起附加光程差 2 S