西安电子科技大学：《大学物理》课程教学讲义（下）10-8 电介质

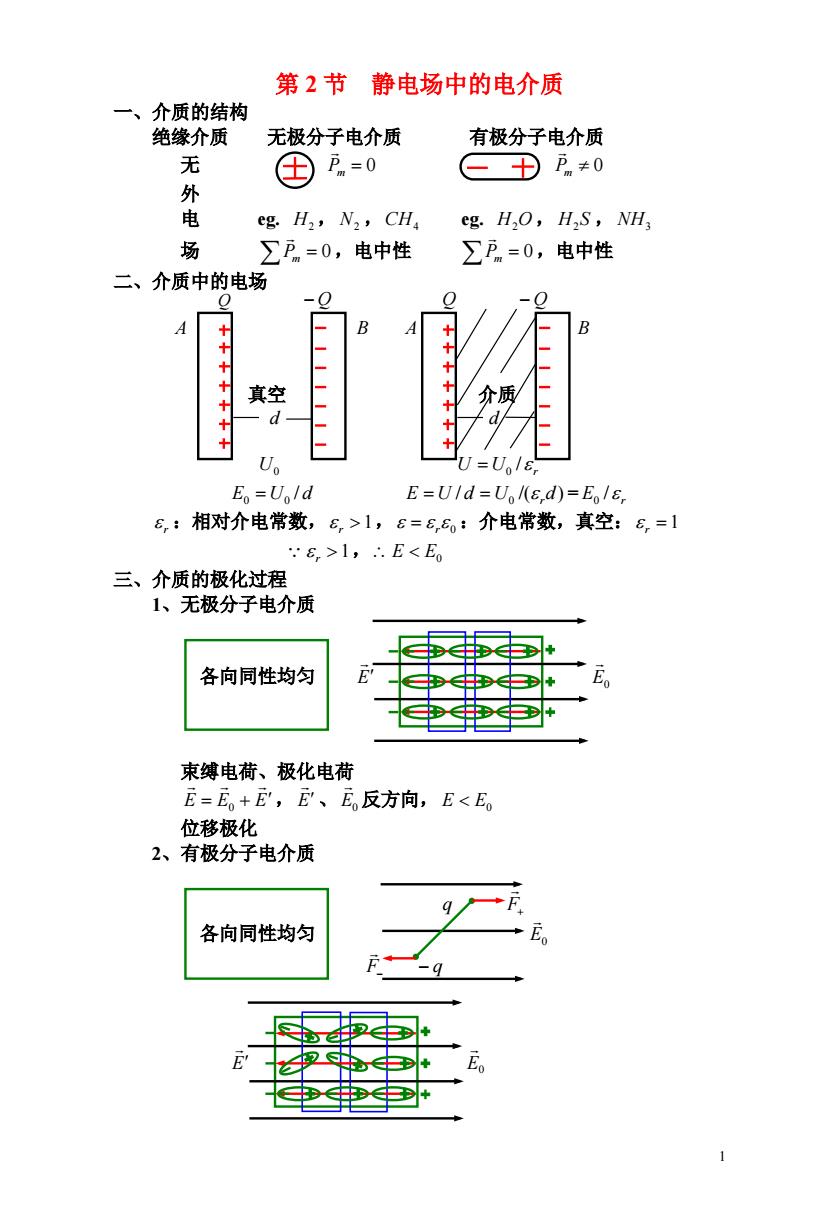
第2节 静电场中的电介质 一、介质的结构 绝缘介质 无极分子电介质 有极分子电介质 无 万m=0 - 卫n≠0 外 电 eg.H2,N2,CHa eg.H,O,H,S,NH 场 ∑万=0，电中性 ∑万=0，电中性 二、介质中的电场 ++ 众质 U J=U E。=Uo/d E=Uld=Ul(s,d)=Eol8 6,:相对介电常数，6>1,6=6，：介电常数，真空：6，=1 E,>1,∴.E<Eo 三、介质的极化过程 1、无极分子电介质 各向同性均匀 束缚电荷、极化电荷 E=E。+E,E、E。反方向，E<E。 位移极化 2、有极分子电介质 9 各向同性均匀

1 第 2 节 静电场中的电介质 一、介质的结构 绝缘介质 无极分子电介质 有极分子电介质 无  0 Pm  Pm  0  外 电 eg. H2 ， N2 ，CH4 eg. H2O， H2S ， NH3 场 Pm  0，电中性 ，电中性  Pm  0  二、介质中的电场 A B A B 真空 介质 d d U0 U U r /  0 E0  U0 / d E  U / d  U0 /( rd) = E r / 0  r ：相对介电常数， r 1，   r 0 ：介电常数，真空： r 1   r 1， E  E0 三、介质的极化过程 1、无极分子电介质 各向同性均匀 E  E0  束缚电荷、极化电荷 E  E  E， 、 反方向，    0 E  E0  E  E0 位移极化 2、有极分子电介质 q F 各向同性均匀 E0  F  q E  E0  Q  Q Q  Q

E=E。+E,E、E。反方向，E<E。 取向极化（为主)+位移极化 四、D的高斯定理 + E=Bo=a (1) E=E+E,E。=g, C,E=E。-E=g-g(2) E080 =g-g,g=-g,=0-g=1- 806,8060 fEs=∑q-o-S--12g 80内 Eo6,E08,内 「65，EdS=∑9，定义：电位移矢量D=6e,E=E E:总电场强度，真空：D=6nE 一D的高斯定理 注意(1)中D=5D.压=∑9，仅与∑9有关，与束缚电荷无关 但D、E与所有电荷及其分布有关 2》E=2D.w-29 有电介质时后者应用更方便 (3)D、E对比： 各向同性均匀电介质：D=65E=E,D=66,E=E D没有具体的物理意义 fEdi=0,Ddi≠0 电荷受力，介质极化，电势、电势差由E决定 电势：Up=∫Edi,电势差Uo=∫E.di 静电场D线的性质： “由正自由电荷发出，终止于负自由电荷，在无自 由电荷区域，D线不能中断，任意两条D线不相交

2 E  E  E， 、 反方向，    0 E  E0  E  E0 取向极化（为主）+位移极化 四、 D 的高斯定理        S r  （1） 0 0   E  r r E E     0 0   E  E  E， ， ， = （2）    0 0 0   E  0   E  E  E  E 0 0 0       = ， = ， = r    0 0 0       r     r         ) 1 (1 r   = = =    内 i S E dS q 0 1    0 ( )    S r S    0  内 f r q  0 1     ，定义：电位移矢量 内 f S rE dS q    0 D rE E         0 E ：总电场强度，真空：  D E   0       的高斯定理 内 f S D dS q   D  注意（1）      仅与 有关，与束缚电荷无关 内 f S D D dS q    内 f q 但 D 、 与所有电荷及其分布有关  E  （2）     内 i S E dS q 0 1         内 f S D dS q   有电介质时后者应用更方便 （3） D 、 对比：  E  各向同性均匀电介质： D rE E ，         0 D   0 rE  E D 没有具体的物理意义     0， L E dl     0 L D dl   电荷受力，介质极化，电势、电势差由 E 决定  电势：    ，电势差 R P P U E dl      Q P PQ U E dl   静电场 D 线的性质：  “由正自由电荷发出，终止于负自由电荷，在无自 由电荷区域， D 线不能中断，任意两条 线不相交。”  D 

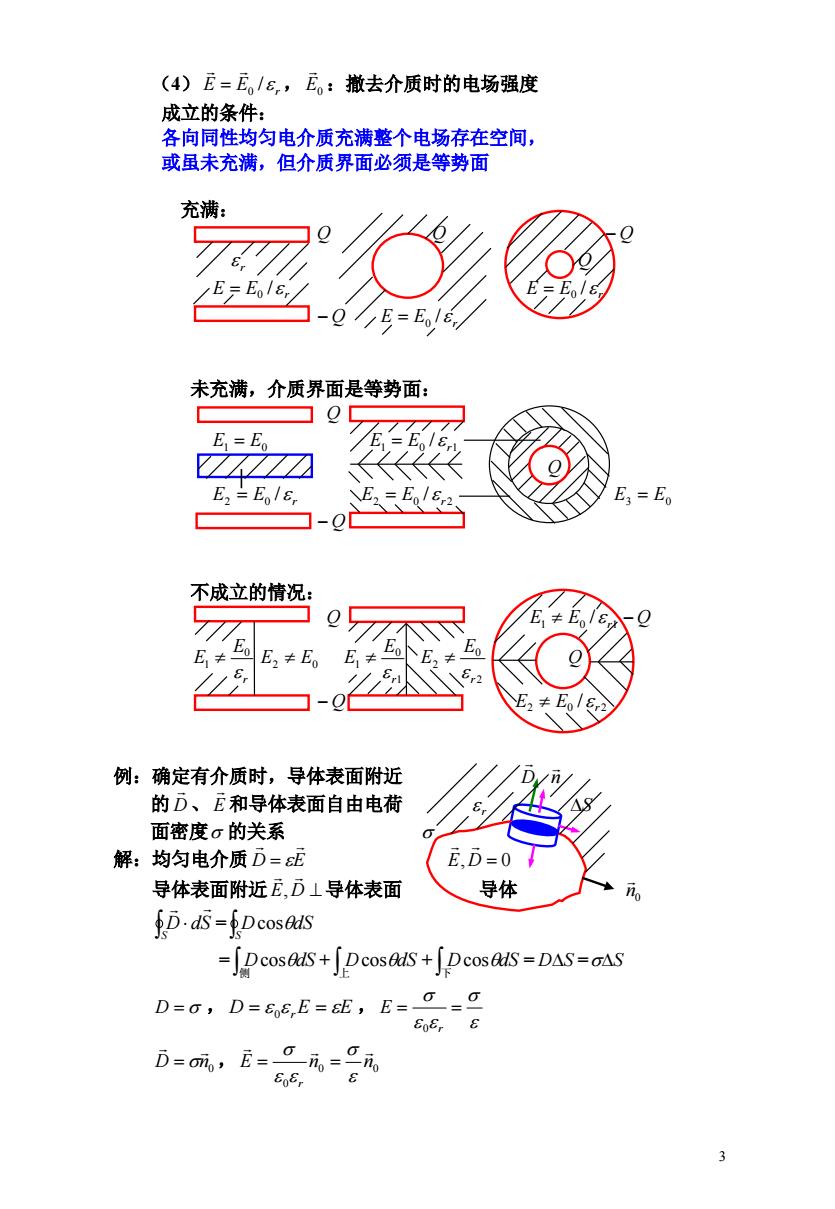
(4)E=E。/8,E。：撤去介质时的电场强度 成立的条件： 各向同性均匀电介质充满整个电场存在空间， 或虽未充满，但介质界面必须是等势面 充满： -QE=E 未充满，介质界面是等势面： E=E ZZZ☑ E3=Eo 不成立的情况： E,卡E E≠ E E,≠E。 E,≠ 例：确定有介质时，导体表面附近 的D、E和导体表面自由电荷 面密度σ的关系 解：均匀电介质D=E E,D=0 导体表面附近E,D1导体表面 导体 D.ds=Dcoses =Dcosais+∫Dcos@dS+∫Dcos&S=DAS=AS D=G,D=E0E,E=SE,E=G= D=m,E=0i,=9元 E06

3 （4） E E0 / r ， ：撤去介质时的电场强度    E0  成立的条件： 各向同性均匀电介质充满整个电场存在空间， 或虽未充满，但介质界面必须是等势面 充满： Q Q  Q r  Q E E r /  0 E E r /  0  Q E E r /  0 未充满，介质界面是等势面： Q E1  E0 1 0 1 / E E r   Q E E r / 2  0 2 0 2 / E E r   E3  E0  Q 不成立的情况： Q 1 0 1 / E E r    Q r E E  0 1  E2  E0 1 0 1 r E E   2 0 2 rE E   Q  Q 2 0 2 / E E r   例：确定有介质时，导体表面附近 D  n  的 D 、 和导体表面自由电荷  E  r  S 面密度 的关系  解：均匀电介质 D E     E,D  0   导体表面附近 E D 导体表面 导体   , n0  =   S D dS   S DcosdS = + + = = 侧 DcosdS 上 DcosdS 下 DcosdS DS S D   ， D   0 rE  E ，        r E 0 D n0 ，    0 0 0 E n n r          

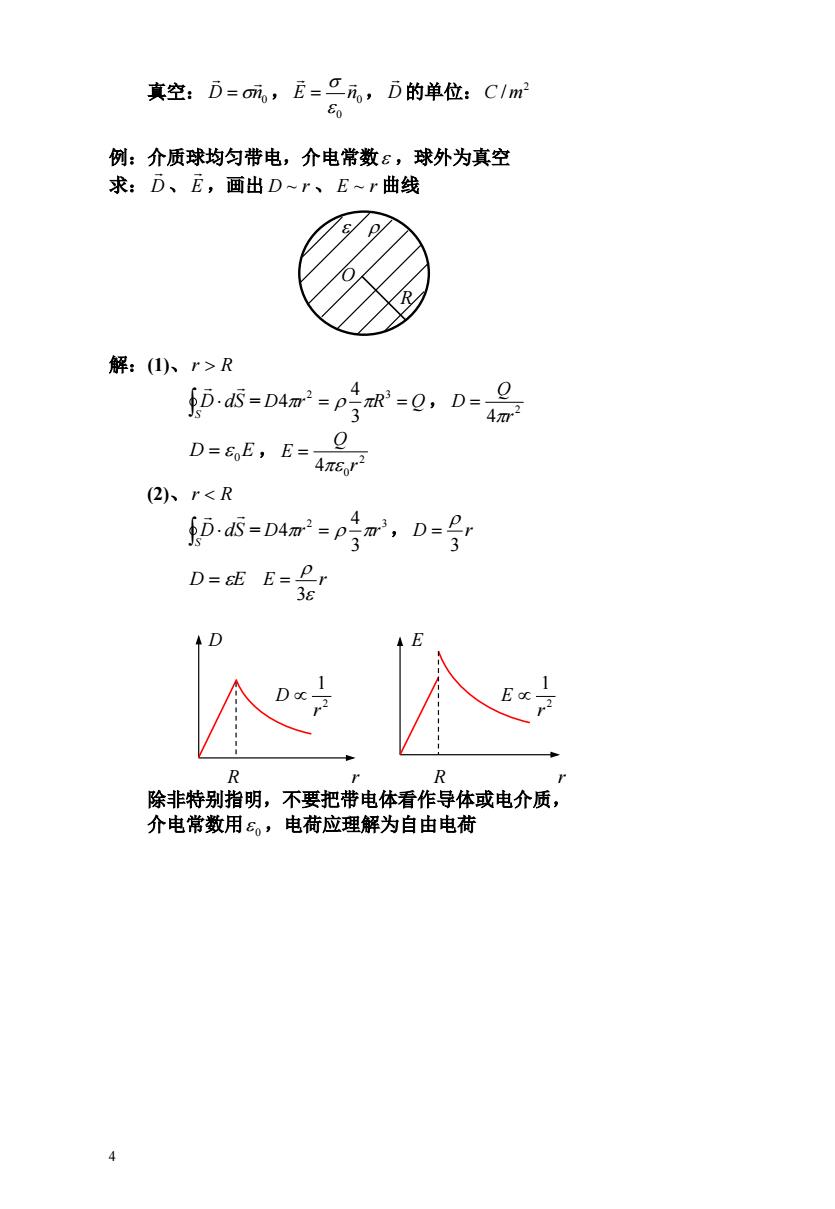
真空：D=om,E=C元，D的单位：C1m2 例：介质球均匀带电，介电常数ε，球外为真空 求：D、E,画出D~r、E~r曲线 2 解：()r>R D.dS-D4m-4R-Q,D=0 2 40.2 D=6E,E=e 4n62 (2)、r<R D.dS=D4m=p m,D= 4 3 D=&EE=Pr D E R R 除非特别指明，不要把带电体看作导体或电介质， 介电常数用8。，电荷应理解为自由电荷 4

4 真空： D n0 ， ， 的单位：     0 0 E n      D  2 C / m 例：介质球均匀带电，介电常数 ，球外为真空 求： D 、 ，画出 、 曲线  E  D ~ r E ~ r   O R 解：(1)、r  R   = ， S D dS   D r  R  Q 2 3 3 4 4   2 4 r Q D   D   0E ， 2 4 0r Q E   (2)、r  R   = ， S D dS   2 3 3 4 D4r   r D r 3   D  E E r   3  D E 2 1 r D  2 1 r E  R r R r 除非特别指明，不要把带电体看作导体或电介质， 介电常数用 0 ，电荷应理解为自由电荷