西安电子科技大学：《大学物理》课程教学讲义（下）12-3 感生电动势与涡旋电场

12一3感生电动势与涡旋电场 一、 涡旋电场假说 例：求矩形回路中的感生电动势 解：Φn)=∫B.=∫BcosQdS n -0, I( ⑧ B 2 =Io sin ot -Kodsinor 2π =d pcosorln dt 2元 产生电动势的非静电力是什么力？从哪里来的？ 祸旋电场假说：随时间变化的磁场一具有闭合力线的电场： 涡旋电场（感应电场)，场强E，非静电场 一段导线：=兵，d1,闭合回路：6=5兵，i=- dt 静电场 涡旋电场 产生原因 静电荷 随时间变化的磁场 电力线 不闭合 闭合 环路定理 fE.di-0 6fEdi=-do 保守场、电势 非保守场，电势X 高斯定理 fE.s=∑q, f瓦，a=0 80内 对q的作用力 F=gE F=gEv fEn=-地 aB dt f瓦·ai<0 涡旋电力线的环绕方向与B满足左手定则 Ev aB 0

1 12—3 感生电动势与涡旋电场 一、涡旋电场假说 例：求矩形回路中的感生电动势 2 l L 解：       S S m (t) B dS BcosdS   n  = l dx， x r l I t r 1 0 2 2 ( )     I t I t sin ( )  0 r B  1 l = ， r r l t I l 0 0 1 2 sin ln 2     x dx x r r l t I l dt d m i 0 0 1 2 cos ln 2            产生电动势的非静电力是什么力？从哪里来的？ 涡旋电场假说：随时间变化的磁场具有闭合力线的电场： 涡旋电场（感应电场），场强 EV ，非静电场  一段导线：    ，闭合回路： L i V E dl          L m i V dt d E dl    静电场 涡旋电场 产生原因 静电荷 随时间变化的磁场 电力线 不闭合 闭合 环路定理   0 L E dl         L m i V dt d E dl    保守场、电势 非保守场，电势 高斯定理     内 i S E dS q 0 1      0 S V E dS   对q 的作用力 F qE    EV F q         L m V dt d E dl   n  t B    =   0 ，        dS t B B dS dt d S S    固定回路 L    L V E dl 0   t B    EV 涡旋电力线的环绕方向与 满足左手定则 t B    EV t B    t B    t B    EV EV

二、涡旋电场的计算 ∮E,di=-Φ。 dt 5H.di=∑1 例：半径为R的无限长 直螺线管内有均匀 磁场B，方向⑧ 设磁场以恒定速率 增加， OB ->0 8 求：E 解： (1)rR Ev 5E,·di=E,2m=-地。 dt =-d（BR2)= -AR2 dt 2ot r 例：无限长直螺线管(R、8、 aB,0) 1× dl 求：直导线ab中的电动势 LoB,hd 解：8a=广瓦ai-cosl=2片 尝山：授尽0，方胸：6,6常电势高 讨论：(1)对于祸旋电场不能引入电势概念，为什么说b端 电势高？ 答：b端积累正电荷，a端积累负电荷 电势概念是针对积累电荷的静电场引入的 2

2 二、涡旋电场的计算      L m V dt d E dl     L H dl    内 I传 例：半径为 R 的无限长 直螺线管内有均匀 磁场 B ，方向  B  设磁场以恒定速率 O EV 增加，  0   t B R r 求： EV 解： t B    （1）r  R，沿电力线积分，n 向外  2 cos 2 ( ) r t B BS dt d dt d E dl E dl E r L m V L V V                    r t B EV    2 1 （2）r  R EV       L m V V dt d E dl E 2r   r 1  2 2 ( ) R t B B R dt d         r R t B EV 1 2 1 2    R r 例：无限长直螺线管（ R 、 B 、 ）   0   t B O R EV l dl 求：直导线ab 中的电动势 解：          b a L b a L V b a L ab V dl r h r t B E dl E dl 2 1 cos ( ) ( ) ( )     = ( / 2) 0，方向 ， 端电势高 2 1 2 1 2 2        l R l t B hl t B a  b b 讨论：（1）对于涡旋电场不能引入电势概念，为什么说b 端 电势高？ 答：b 端积累正电荷，a 端积累负电荷 电势概念是针对积累电荷的静电场引入的 r  a b h 

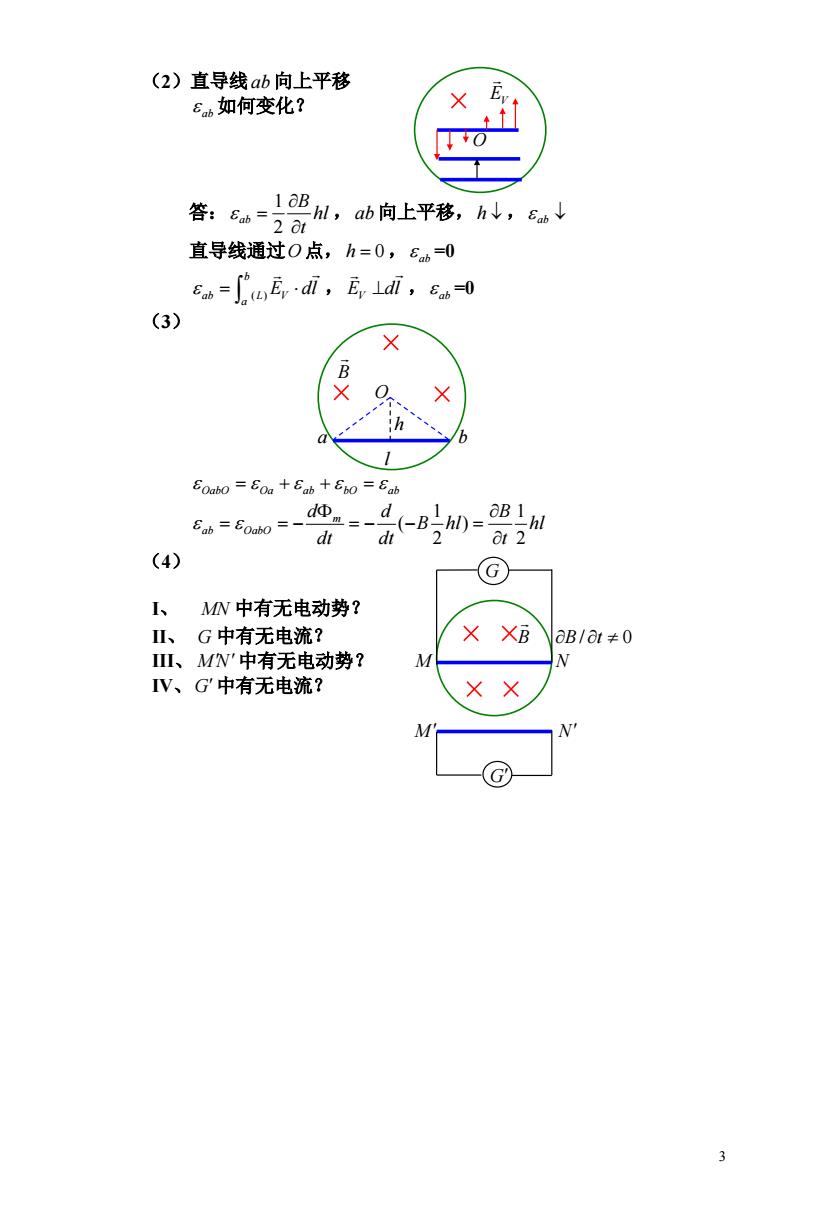
(2)直导线ab向上平移 6b如何变化？ 答器，6肉上平移，A,小 直导线通过O点，h=0,6b=0 6b=∫6En·di，E,ldi，6b-0 (3) B h a b 1 E0abo=Eoa+￡ab+Ebo=￡ab Sab E0abo = _=-d(-B-n)-5 d dt t2 (4) G I、 MW中有无电动势？ Ⅱ、G中有无电流？ X XB VaB/at≠0 I、MN'中有无电动势？ N IV、G中有无电流？ X× 3

3 （2）直导线ab 向上平移 如何变化？ ab  答： hl ， 向上平移， ， t B ab    2 1  ab h   ab  直导线通过O点，h  0， ab =0 ， ， =0    b a ab L V E dl   ( )  EV dl  ab  （3） B  O a b l OabO Oa ab bO ab          hl t B B hl dt d dt d m ab OabO 2 1 ) 2 1 (             （4） I、 MN 中有无电动势？ II、 G 中有无电流？ B  B/ t  0 III、 M N中有无电动势？ M N IV、G中有无电流？ M  N G G h O EV

例： I(t)=le a 1=0时，动边与左边重合 求：任意时刻矩形框中的ε 解：取回路绕行正方向顺时针 ④m=JB.a=[Bcos@dS I(t)=Ioe-2 - vtdx a =Holoe -viIn a+b dx 2n =Holo Ina+b (te), 2πa =-bina+bea+-2e”] 6=-di 2 a =Lolov Inatbe em(t-1) 2πa -1>0,8,>0,顺时针；1-1<0,6，<0，逆时针 计算电动势的小结： (1)磁场恒定不变，回路或其一部分运动：动生电动势 一段导线：6b=×B0 闭合回路：8=50×)，6= dΦm d (2)磁场随时间变化，回路不动： 感生电动势 一段导线：6=∫瓦，·di 闭合回路：6=瓦·d,6=- dΦ dt (3)磁场随时间变化，且回路或其一部分又运动：既有感 生电动势，又有动生电动势，最好使用：￡=- dt 4

4 例： t I t I e   0 ( ) a b v vt t  0时，动边与左边重合 求：任意时刻矩形框中的 i  解：取回路绕行正方向顺时针       S S m B dS BcosdS   t I t I e   0 ( ) = vtdx ， x a b I t a    2 ( ) 0 a = ， a a b vt I e t   ln 2 0 0    dx v = ln ( )， 2 0 0 t te a I v a b      vt = dt d m i     ln [ ( ) ] 2 0 0 t t e t e a I v a b            = ln ( 1) 2 0 0    e t a I v a b t     t 1  0 ， i  0，顺时针；t 1  0 ， i  0，逆时针 计算电动势的小结： （1）磁场恒定不变，回路或其一部分运动：动生电动势 一段导线： V B dl b a L ab        ( ) ( )  闭合回路：     ， L V B dl     ( ) dt d m i     （2）磁场随时间变化，回路不动：感生电动势 一段导线：    L i V E dl    闭合回路：    ， L i V E dl    dt d m i     （3）磁场随时间变化，且回路或其一部分又运动：既有感 生电动势，又有动生电动势，最好使用： dt d m i     x x