12一6磁场的能量 一、自感储能 i:0→1 1,6=-L dt Ub=-6,=L4 +di,dA=Uaidi=L di idi Lidi dt 4=a4=h=r 自感储能公式(对任意线圈都成立),以.=C少2 二、磁场能量 n,>>R 磁能分布在磁场中 L=m21πR2 W.= 2 号amar-iml-l,laR -2BHV 磁场能量密度:W=d形- BH=1B21 2 2 均匀磁场: W =w V 非均匀磁场:形。=W=2Bd 例:一段载流同轴电缆 R 1>>R,R 求:磁能及L,(山导体≈) 1
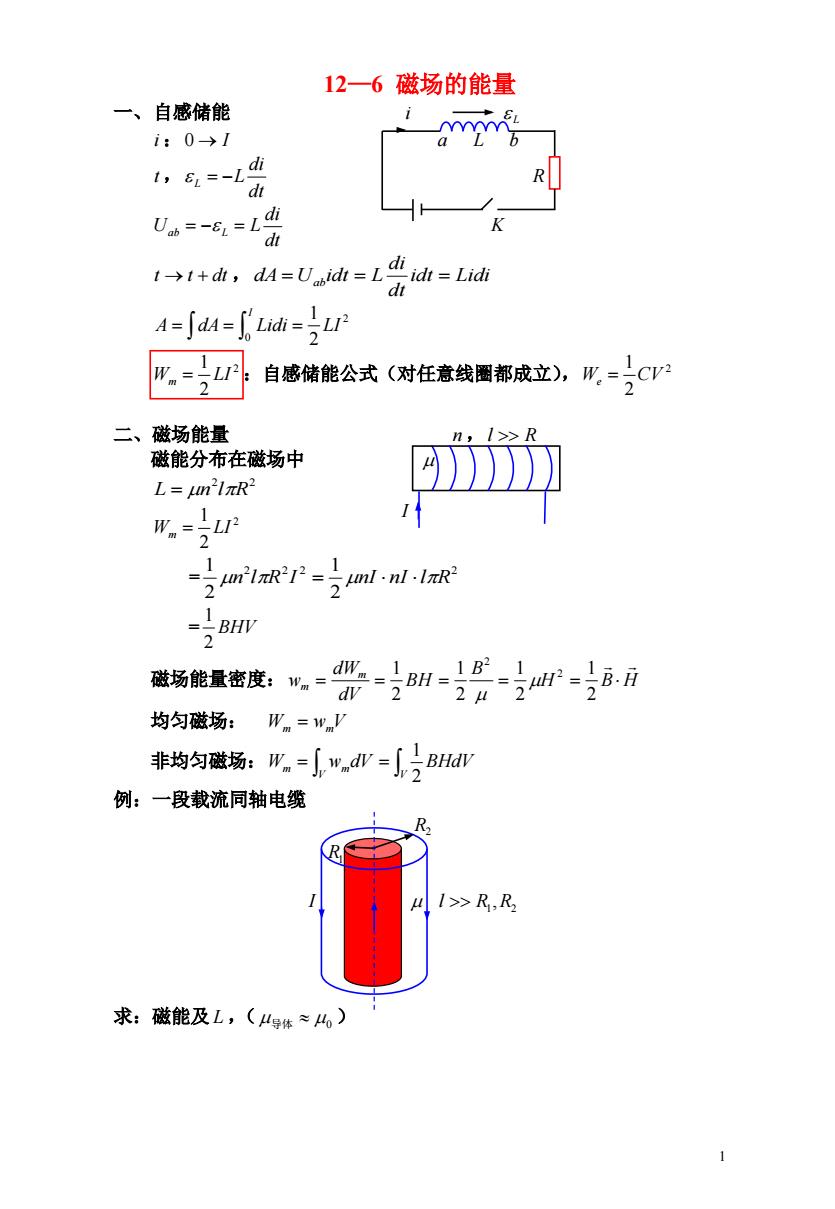
1 12—6 磁场的能量 一、自感储能 i L i :0 I a L b t , dt di L L R dt di Uab L L K t t dt , idt Lidi dt di dA Uab idt L 2 0 2 1 A dA Lidi LI I 2 :自感储能公式(对任意线圈都成立), 2 1 W LI m 2 2 1 We CV 二、磁场能量 n ,l R 磁能分布在磁场中 2 2 L n lR 2 2 1 W LI m = 2 2 2 2 2 1 2 1 n lR I nI nI lR = BHV 2 1 磁场能量密度: H B H B BH dV dW w m m 2 1 2 1 2 1 2 1 2 2 均匀磁场: Wm wmV 非均匀磁场: V V Wm wmdV BHdV 2 1 例:一段载流同轴电缆 R2 R1 I 1 2 l R ,R 求:磁能及 L ,( 导体 0 ) I

Ir rR 0 r>R w。=pw.a" d 薄圆柱壳,dW=2mdrl R:L4l2 见。R2nd+短atM ln 16π4πR 所r,1=2现小是4丛n是 8π2πR 2
2 解: , 2 2 2 2 1 1 0 2 2 r R R r R r I r R R Ir H 2 2 2 2 2 2 4 1 1 2 2 2 0 2 0 8 8 2 1 r R R r R r I r R R I r wm H V Wm wmdV r dr 薄圆柱壳,dV 2rdrl rdrl r I rdrl R I r W R R R m 2 8 2 8 2 1 1 2 2 2 0 4 1 2 2 2 0 l = 1 2 2 2 0 ln 16 4 R I l I l R 2 , 2 1 W LI m 1 2 0 2 ln 8 2 2 / R l l R L W I m