
第4节 薄膜干涉 (1)等厚干涉(2)等倾干涉 一、等厚干涉的一般理论 n 1、光路图 厚度不均匀薄膜n, i:入射角 薄膜上下表面产生的两条反射光 在薄膜上表面相遇相干迭加 B n: .2 2、光程差6=n,(AB+BC)-nDC,6=2eVn-nsin2i n2>n1,n3,光线2有半波损失,光线1没有,应加上1/2 n2n2>m,光线2和光线1都没有半波损失,不加1/2 8=2e-sin+ 3、等厚干涉条纹 i一定,6=6(e) k入 k∈N 干涉加强 δ-2e√n-nsin2i+ 入一定:反射光干涉加强时,透射光干涉相消 反射光干涉相消时,透射光干涉加强 例:用日光垂直照射空气中e=0.40m、折射率为1.50的玻璃片 求:可见光范围,哪些波长的光反射加强、哪些波长的光透射加强? 解:反射加强条件6=2e店-川sin7+?=2,e+ 2 =k A=Ame 2k-1 k=3,7=4×1.50×0.40×10-6 =0.48m 2×3-1 透射加强条件(反射光相消条件) 6=2eV居-isin2i=2n,e=ka,元=2ne k k=2,2=0.60m;k=3,=0.40m 1
1 第 4 节 薄膜干涉 (1)等厚干涉(2)等倾干涉 一、等厚干涉的一般理论 S n1 1、光路图 2 2 1 厚度不均匀薄膜 2 n D i :入射角 C 2 n 薄膜上下表面产生的两条反射光 e 在薄膜上表面相遇相干迭加 B n3 2、光程差 n2 (AB BC) n1 DC , e n n i 2 2 1 2 2 2 sin n2 n1 ,n3 ,光线 2 有半波损失,光线 1 没有,应加上 / 2 n2 n1 ,n3 ,光线 2 没有半波损失,光线 1 有,应加上 / 2 n1 n2 n3 ,光线 2 和光线 1 都有半波损失, 不加 / 2 n1 n2 n3 ,光线 2 和光线 1 都没有半波损失,不加 / 2 2 2 sin 2 2 1 2 2 e n n i 3、等厚干涉条纹 i 一定, (e) ( ) 干涉相消 干涉加强 k k N k k N e n n i 2 2 2 1 2 sin 2 2 1 2 2 k :干涉级,k 的取值必须保证e 0 干涉条纹形状与薄膜等厚线形状相同 说明:(1)用日光照射薄膜,呈现彩色条纹 (2)从薄膜上方看到的是反射光的干涉 从薄膜下方看到的是透射光的干涉 透射光光程差 2 2 sin 2 2 1 2 2 e n n i 一定:反射光干涉加强时,透射光干涉相消 反射光干涉相消时,透射光干涉加强 例:用日光垂直照射空气中e 0.40m、折射率为1.50的玻璃片 求:可见光范围,哪些波长的光反射加强、哪些波长的光透射加强? 解:反射加强条件 = 2 2 2 2 sin 2 2 2 1 2 2 e n n i n e k = 2 1 4 2 k n e k 3, 0.48m 2 3 1 4 1.50 0.40 10 6 透射加强条件(反射光相消条件) e n n i n2e = , = 2 2 1 2 2 2 sin 2 k k n e 2 2 k 2 , 0.60m ;k 3, 0.40m i 1 A

二、几种重要的薄膜干涉 1、劈尖干涉 用波长入的单色光垂直照射劈尖 i=0 δ-2eVn-nsin2i+< 空气劈尖 d=2e+ (空气中的玻璃劈尖6=2ne+2) [k k=1,2,3,…明纹 d=2e+ 22k+1子k=0,12,暗纹 玻璃劈尖 明纹中心下面空气薄膜厚度e=2k-l,上,3,5, 4 4 暗纹中心下面空气薄膜厚度e=k以, 1 0, 2,, 等厚线是平行棱边的直线 条纹是平行棱边的直条纹 相邻两明纹或两暗纹下面 空气薄膜厚度差△e=1/2 相邻两明纹或两暗纹的 棱边 距离l=△e/sin0= 0 2sin 日:劈尖的夹角,条纹均匀分布 日↓,1个条纹容易分辨,日个,1J 用途:已知入,测量1,求8;已知B,测量1,求入; 检验玻璃表面是否平整 棱边处是一暗纹,6=2e+ =, 是半波损失的有力证据 22 空气中的玻璃劈尖:△e= ,1= 2n 2nsin0 例:L=28.880mm,用波长 1=0.5893um的光垂直 照射劈尖,测得第一条 明纹到第31条明纹的 距离为4.295mm L 求:金属丝的直径D 解:相邻两明纹的距离1=4295 =0.14317mm 31-1 /= 2sinθ sine=A 21 D≈L1g8≈Lsin0=LA=0.05944mm 21 2
2 二、几种重要的薄膜干涉 2 2 1 1、劈尖干涉 1 用波长 的单色光垂直照射劈尖 e i 0 空气劈尖 2 2 sin 2 2 1 2 2 e n n i (空气中的玻璃劈尖 ) 2 2 e 2 2 ne 玻璃劈尖 暗纹 明纹 0,1,2, 2 (2 1) 1,2,3, 2 2 k k k k e 明纹中心下面空气薄膜厚度 , , , , 4 2 1 k e 4 1 4 3 4 5 暗纹中心下面空气薄膜厚度e k , , , , 2 1 0 2 1 等厚线是平行棱边的直线 l 条纹是平行棱边的直条纹 相邻两明纹或两暗纹下面 空气薄膜厚度差e / 2 e 相邻两明纹或两暗纹的 棱边 距离 0 2sin l e /sin 4 1 2 1 4 3 4 5 :劈尖的夹角,条纹均匀分布 ,l 条纹容易分辨, ,l 用途:已知 ,测量l ,求 ;已知 ,测量l ,求 ; 检验玻璃表面是否平整 棱边处是一暗纹, ,是半波损失的有力证据 2 2 2 e 空气中的玻璃劈尖: ,n e 2 2nsin l 例: L 28.880mm ,用波长 0.5893m的光垂直 照射劈尖,测得第一条 D 明纹到第 31 条明纹的 距离为4.295mm L 求:金属丝的直径 D 解:相邻两明纹的距离 l 0.14317mm 31 1 4.295 , 2sin l 2l sin =l D Ltg L L 2 sin 0.05944mm

a(→ 圆柱向右移动,条纹如何变化? v 条纹间距↓,向右移动 L↓,条纹如何变化? 条纹间距↓ N=L/cos0 2L. /2sin6元g9=2d,-d) 2 下面几种情况条纹如何变化? ---- 例:用波长入的单色平行光垂直照射由 平板玻璃和工件形成的空气劈尖, 观察干涉条纹弯曲,弯曲部分的顶 部恰与左边条纹直线部分相切,说 明工件上有一凹槽,深度入/2 解;条纹是空气薄膜的等厚线 平板玻璃 某条纹弯曲部分的顶部下面空气薄膜厚度 与同一条纹上直线部分下面空气薄膜厚度相同 工件上必有一凹槽,深度等于相邻两明纹直线 工件 部分对应的空气薄膜厚度差1/2 2、增透膜与增反膜 反射光的光程差 空气n 6=2n2e+ 薄膜n2 如果反射光干涉加强,增反膜 玻璃片n3 如果反射光干涉相消,增透膜 例:设n=1,m2=1.38,n=1.55,用元=550nm的黄绿光垂直 照射薄膜,若使反射光强最小 求:薄膜最小厚度 解:=2ne 6=2n,e=(2k+1)月 2k+122k=0,e=1=550 e =100nm 4n2 4n24×1.38 注:n、n2、n,、e给定,薄膜只对特定波长的光增透或增反 若用日光照射,反射光中缺少黄绿光,反射光呈蓝紫色 3
3 d2 圆柱向右移动,条纹如何变化? L 条纹间距 ,向右移动 L ,条纹如何变化? 条纹间距 ( ) 2 2 / 2sin / cos d2 d1 tg L L N 下面几种情况条纹如何变化? V V 例:用波长 的单色平行光垂直照射由 平板玻璃和工件形成的空气劈尖, 观察干涉条纹弯曲,弯曲部分的顶 部恰与左边条纹直线部分相切,说 明工件上有一凹槽,深度 / 2 解;条纹是空气薄膜的等厚线 平板玻璃 某条纹弯曲部分的顶部下面空气薄膜厚度 与同一条纹上直线部分下面空气薄膜厚度相同 工件上必有一凹槽,深度等于相邻两明纹直线 工件 部分对应的空气薄膜厚度差 / 2 2、增透膜与增反膜 反射光的光程差 空气 n1 薄膜 2 2 2 n e 2 n 如果反射光干涉加强,增反膜 玻璃片n3 如果反射光干涉相消,增透膜 例:设n1 1,n2 1.38 ,n3 1.55,用 550nm的黄绿光垂直 照射薄膜,若使反射光强最小 求:薄膜最小厚度 解: n e 2 2 2n2e = 2 (2 1) k , , 4 2 2 1 n k e k 0 nm n e 100 4 1.38 550 4 2 min 注:n1 、n2 、n3 、e 给定,薄膜只对特定波长的光增透或增反 若用日光照射,反射光中缺少黄绿光,反射光呈蓝紫色 d1 e

3、牛顿环 k入 k=1,2,3,…明纹 8=2e+ 2 (2k+D2 k=01,2,…暗纹 k:干涉级 空气薄膜的等厚线是圆环 条纹是圆环 明环下空气薄膜厚度e-2k-l, 3 , , 4 4 4 4 1 1 暗环下空气薄膜厚度e=。k2, 0, 2 2 相邻两明环或暗环下面空气薄膜厚度差: 2 r2 r2=e(2R-e)≈2eR,e= 2R r2. k入 明环半径r=k-2迟 k=1,2,3,… 6=2e+ 2R2 2+ 暗环半径r=√kR k=01,2, 中心是暗斑(0级暗纹) k个,r个 条纹分布不均匀,向外越来越密 例:用2=5893A的黄光观察牛顿环,看到 第k级暗环半径r=4mm,第k+5级暗环半径r+5=6mm 求:凸透镜半径R及 解:1=VR,s=欣+5,-k+5=1+,-2-三 -762-4=4,R=是=4x10-2 5×42 k74×5893x10-0=6.79m 思考题 (1)把牛顿环装置放在水中,条纹如何变化? (n水=1.33,n孩=1.52) k入 明环半径r= 8=2nke+ K(k-)iRIns 2 R 2 2k+ 暗环半径r=√kR/n* 条纹变密 (2)凸透镜向上移动, 条纹如何变化? 条纹向中心收缩
4 3、牛顿环 O 暗纹 明纹 0,1,2, 2 (2 1) 1,2,3, 2 2 k k k k e R k :干涉级 r e 空气薄膜的等厚线是圆环 条纹是圆环 明环下空气薄膜厚度 , , , , 4 2 1 k e 4 1 4 3 4 5 暗环下空气薄膜厚度e k , , , , 2 1 0 2 1 相邻两明环或暗环下面空气薄膜厚度差: 2 r 2 e(2R e) 2eR , R r e 2 2 0,1,2, 2 (2 1) ) 1,2,3, 2 1 ( 2 2 2 2 k r k R k k r k R k R r e 暗环半径 明环半径 中心是暗斑(0 级暗纹) k ,r 条纹分布不均匀,向外越来越密 例:用 的黄光观察牛顿环,看到 5893A 第k 级暗环半径rk 4mm ,第k 5级暗环半径rk5 6mm 求:凸透镜半径 R 及k 解:rk kR ,rk5 (k 5)R , , k k k r r k k 5 1 5 2 2 5 r k r r k k k 5 2 2 2 5 4 , 6 4 5 5 4 2 2 2 2 2 5 2 k k k r r r k m k r R k 6.79 4 5893 10 (4 10 ) 10 2 3 2 思考题 (1)把牛顿环装置放在水中,条纹如何变化? ( n水 1.33,n玻 1.52 ) 水 水 水 水 暗环半径 明环半径 k r k R n k r k R n R n r n e / 2 (2 1) ) / 2 1 ( 2 2 2 2 条纹变密 (2)凸透镜向上移动, 条纹如何变化? 条纹向中心收缩
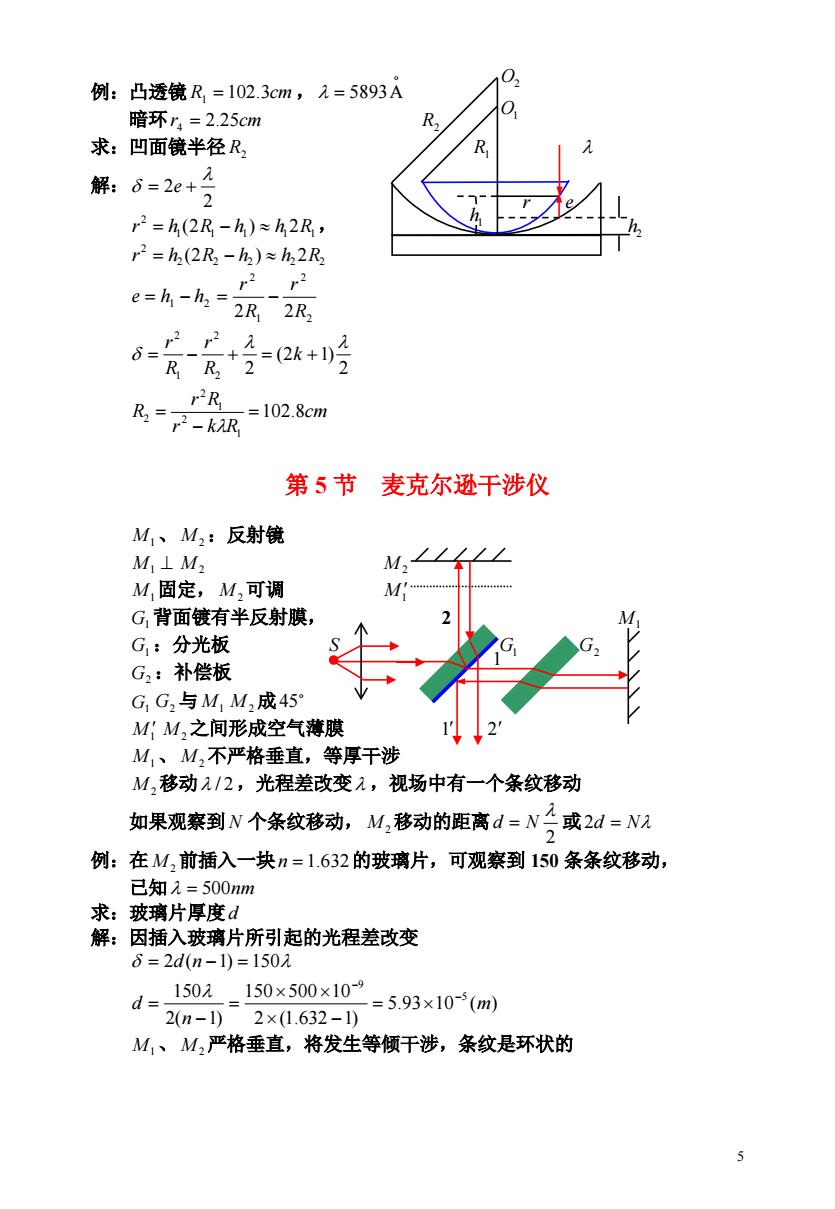
02 例:凸透镜R=102.3cm,1=5893A 暗环r=2.25cm R 求:凹面镜半径R R 解:6=2e+ 2 r2=h(2R-h)≈h2R, r2=h(2R2-h2)≈h22R e=h-h= r22 2R 2R, =2-主+号-0+吟 RR2 r2R R,=,2-kR =102.8cm 第5节 麦克尔逊干涉仪 M1、M2:反射镜 M1⊥M2 M固定,M,可调 G,背面镀有半反射膜, G,:分光板 G2:补偿板 G,G2与M1M2成45 MM,之间形成空气薄膜 M1、M,不严格垂直,等厚干涉 M移动1/2,光程差改变入,视场中有一个条纹移动 如果观察到N个条纹移动,M,移动的距离d=N或2d=N7 例:在M,前插入一块n=1.632的玻璃片,可观察到150条条纹移动, 已知2=500nm 求:玻璃片厚度d 解:因插入玻璃片所引起的光程差改变 6=2d(n-1)=150入 d=1502=150×500×109 =5.93×10-5(m) 2(n-1)2×(1.632-1) M1、M2严格垂直,将发生等倾干涉,条纹是环状的 5
5 例:凸透镜 R 102.3cm , 1 5893A 暗环r 2.25cm 4 R2 求:凹面镜半径 R2 R1 解: 2 2 e , 1 1 1 1 1 2 r h (2R h ) h 2R h2 2 2 2 2 2 2 r h (2R h ) h 2R 2 2 1 2 1 2 2 2R r R r e h h 2 (2 1) 2 2 2 1 2 k R r R r cm r k R r R R 102.8 1 2 1 2 2 第 5 节 麦克尔逊干涉仪 M1 、 M 2 :反射镜 M1 M 2 M 2 固定, 可调 M1 M 2 M1 背面镀有半反射膜, 2 G1 M1 :分光板 G1 S G1 G2 G2 :补偿板 G1 G2 与 M1 M 2 成 45 之间形成空气薄膜 M1 M 2 1 2 M1 、 M 2 不严格垂直,等厚干涉 M 2 移动 / 2,光程差改变 ,视场中有一个条纹移动 如果观察到 N 个条纹移动, M 2 移动的距离 或2 d N 2d N 例:在 M 2 前插入一块n 1.632的玻璃片,可观察到 150 条条纹移动, 已知 500nm 求:玻璃片厚度d 解:因插入玻璃片所引起的光程差改变 2d(n 1) 150 5.93 10 ( ) 2 (1.632 1) 150 500 10 2( 1) 150 5 9 m n d M1 、 M 2 严格垂直,将发生等倾干涉,条纹是环状的 h1 r e O2 O1 1