
第4节麦克斯韦分子速率分布律 一、麦率 单个分子的速率可以取0~∞之间的任何数值 平衡状态下,大量气体分子按照速率的分布遵守完全确定 的统计规律 △N,△N,△N, 0y, V2 V3 1 AN AN2 AN3 N N N 0°C 氧气分子速率分布 速率区间(m/s) △ ×100% 0-100 1.4% 100-200 8.1% 200-300 16.5% 300-400 21.4% 400-500 20.6% 500-600 15.1% 600-700 9.2% 700-800 4.8% 800-900 2.0% 900-0 0.9% 速率区间v~v+dw ↑,dN↑ dN ↑个,N dN a dy 0 v+dy N 小相同,心八与速率区间取在哪个速率,附近有关 如速率在100-100+和200-200+h中不同 -fw小,f):分子速率分布函数 dN 心)一:在速率,附近单位速率区间中的分子数 占总分子数的比率 f()=4π( m)3/2v2e2m2 2n 麦克斯韦分子速率分布函数 1
1 第 4 节 麦克斯韦分子速率分布律 一、麦~率 单个分子的速率可以取0 ~ 之间的任何数值 平衡状态下,大量气体分子按照速率的分布遵守完全确定 的统计规律 N1 N2 N3 0 , , 1 v 2 v 3 v v N N1 N N2 N N3 0 C 氧气分子速率分布 速率区间(m/s) 100% N N 0~100 1.4% 100~200 8.1% 200~300 16.5% 300~400 21.4% 400~500 20.6% 500~600 15.1% 600~700 9.2% 700~800 4.8% 800~900 2.0% 900~ 0.9% 速率区间v ~ v dv dv ,dN dN , 0 N dN dv N dN v N dN v dv v dv相同, 与速率区间取在哪个速率 附近有关 N dN v 如速率在 100~100+dv 和 200~200+dv 中 不同 N dN = , :分子速率分布函数 N dN f (v)dv f (v) f (v) = :在速率 附近单位速率区间中的分子数 Ndv dN v 占总分子数的比率 f (v) = mv kT v e kT m / 2 1 3/ 2 2 2 ) 2 4 ( 麦克斯韦分子速率分布函数
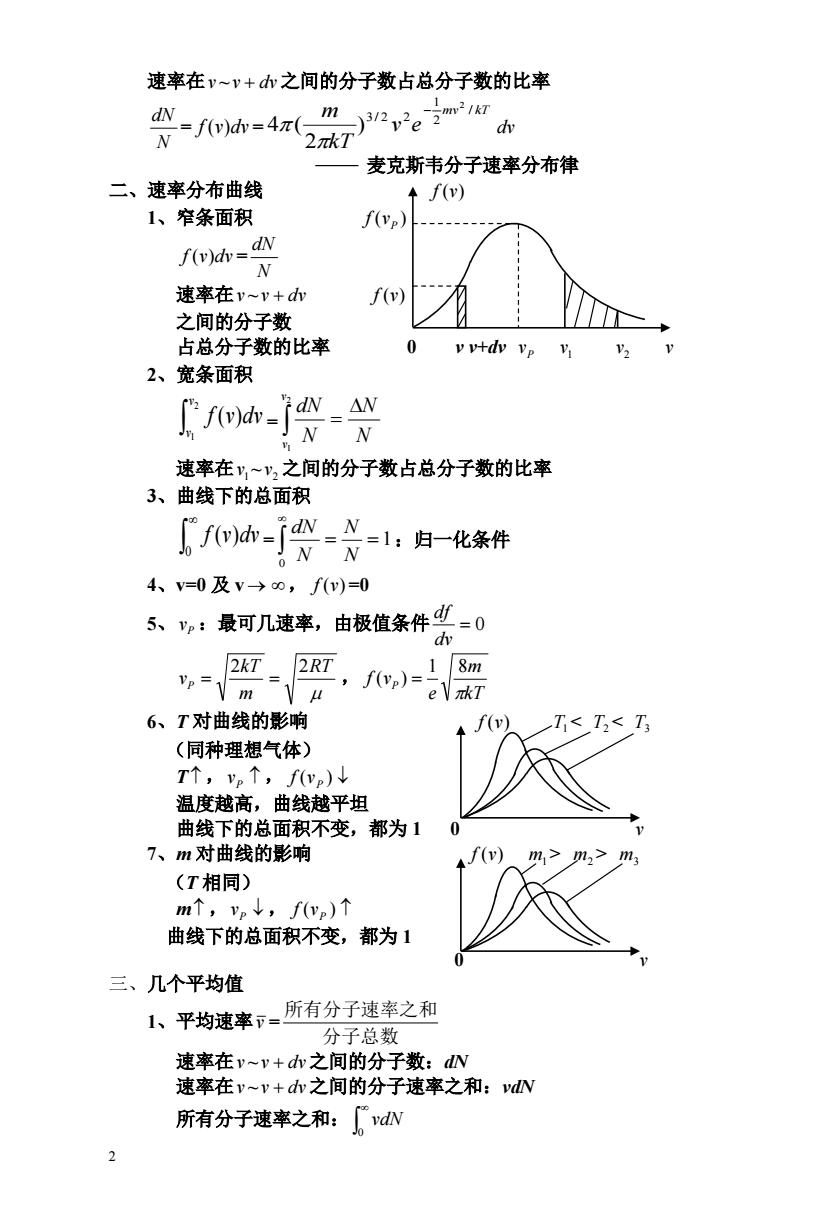
速率在v~v+之间的分子数占总分子数的比率 dN-f(v)dv=4n( m 32p2e2m21 πkT 麦克斯韦分子速率分布律 二、速率分布曲线 f(v) 1、窄条面积 f(vp) I(v)dv=dN N 速率在v~v+dw f(v) 之间的分子数 占总分子数的比率 2、宽条面积 (dvfaw N 速率在y~y,之间的分子数占总分子数的比率 3、曲线下的总面积 h-j货- =1:归一化条件 4、v=0及v→0,f(v)=0 5、:最可几速率,由极值条件=0 2kT 2RT 18m VP=1 m u 6、T对曲线的影响 、f(v)Tm,>m (T相同) m个,vp↓,f(yp)个 曲线下的总面积不变,都为1 三、几个平均值 1、平均速率下=所有分子速率之和 分子总数 速率在v~v+dw之间的分子数:dW 速率在v~v+d之间的分子速率之和:vdW 所有分子速率之和:vdW 2
2 速率在v ~ v dv之间的分子数占总分子数的比率 = = N dN f (v)dv mv kT v e kT m / 2 1 3/ 2 2 2 ) 2 4 ( dv 麦克斯韦分子速率分布律 二、速率分布曲线 f (v) 1、窄条面积 ( ) P f v f (v)dv = N dN 速率在v ~ v dv f (v) 之间的分子数 占总分子数的比率 0 v v+dv P v 1 v 2 v v 2、宽条面积 = 2 1 ( ) v v f v dv N N N dN v v 2 1 速率在v1 ~ v2 之间的分子数占总分子数的比率 3、曲线下的总面积 = :归一化条件 0 f (v)dv 1 0 N N N dN 4、v=0 及 v , f (v) =0 5、vP :最可几速率,由极值条件 0 dv df , RT m kT vP 2 2 kT m e f vP 1 8 ( ) 6、T 对曲线的影响 f (v) T1 m2 > m3 (T 相同) m ,vP , f (vP ) 曲线下的总面积不变,都为 1 0 v 三、几个平均值 1、平均速率v = 分子总数 所有分子速率之和 速率在v ~ v dv之间的分子数:dN 速率在v ~ v dv之间的分子速率之和:vdN 所有分子速率之和: 0 vdN

vv(d-m T 8RT πu 2、=所有分子速率平方之和 分子总数 所有分子速率平方之和: [rdn -ff m 3kT 3RT 三个特征速率: J(v) 2kT 8kT 3kT <= eV=Vm m vp:讨论速率分布问题 下:讨论分子碰撞问题 √厅:计算分子平均平动动能 Vp V 3、平均平动动能 五x=caw=6fww=2mfoh=号7 4、速率v的任意函数g(v)的平均值 g=g(v)f(v)dv 指出下列各式的物理意义: f(v)dv,Nf(v)dv,["f(v)dv,"Nf(v)dv N(dv,m(dv,Nf(dv 0h-代:速率在+小之间的分子数 占总分子数的比率 Nf(v)d=dN:速率在v~v+d之间的分子数 0-兴: 速率在0~"p之间的分子数占总分子数的比率 ∫Nf(v)-N=AN:速率在y~,之间的分子数 0N(v)=N:分子总数 2mfv)d:分子的平均平动动能 3
3 RT m kT vdN vf v dv N v 8 8 ( ) 1 0 0 2、 =2 v 分子总数 所有分子速率平方之和 所有分子速率平方之和: 0 2 v dN m kT v dN v f v dv N v 3 ( ) 1 0 2 0 2 2 RT m kT v 2 3 3 三个特征速率: f (v) < < m kT vP 2 m kT v 8 m kT v 2 3 vP :讨论速率分布问题 v :讨论分子碰撞问题 :计算分子平均平动动能 0 2 v P v v v 3、平均平动动能 dN f v dv mv f v dv kT N K K K 2 3 ( ) 2 1 ( ) 1 0 2 0 0 4、速率v 的任意函数 g(v)的平均值 0 g g(v) f (v)dv 指出下列各式的物理意义: f (v)dv , Nf (v)dv , , Pv f v dv 0 ( ) 2 1 ( ) v v Nf v dv , , 0 Nf (v)dv 0 2 ( ) 2 1 mv f v dv 2 1 ( ) 2 1 2 v v N mv f v dv f (v)dv = :速率在 之间的分子数 N dN v ~ v dv 占总分子数的比率 Nf (v)dv = dN :速率在v ~ v dv 之间的分子数 = = : Pv f v dv 0 ( ) Pv N dN 0 N N 速率在0 ~ vP 之间的分子数占总分子数的比率 = :速率在 之间的分子数 2 1 ( ) v v Nf v dv 2 1v v dN N 1 ~ 2 v v = :分子总数 0 Nf (v)dv N :分子的平均平动动能 0 2 ( ) 2 1 mv f v dv 2 v

Nmfo)h-2maN:速率在%之间 的分子的平动动能之和 第5节玻耳兹曼分布律 一、重力场中粒子按高度的分布 大气,平衡态,温度T PV=vRT不成立 h+dh P+dp,n+dn P=nkT成立 h P,n dP=-pgdh (1) p:空气质量密度 p=nm,m:空气分子质量 Po,no dP=kTdn (2) kTdn =-pgdh =-nmgdh dh,In n=- gh Jo kT no kT mgh =8h n=noe kT =noe RT h↑,nJ mgh mgh 煜h P=nkT nokTe KT Poe KT Poe RT 等温气压公式 h↑,P↓ 高度计 例:求大气中n相差一倍的两处的高度差 已知:空气4=28.97×10-3kg,T=300K ughz 解:h处,n1=noe RT,h处,n2=noe h>h, ,-gh,-h)=-ln2 n =2’ RT 6-么 RT1n2=6.10×10m g 二、玻耳兹曼分布率 m”ne产,n=m,e号 mgh no --T→0 (适用于任意的保守力场) T'>T Ep:分子势能 n:势能零点处的分子数密度 Ep sp↑,n↓;T个,n个;T→o,n→no 4
4 = :速率在 之间 2 1 ( ) 2 1 2 v v N mv f v dv mv dN v v 2 1 2 2 1 1 ~ 2 v v 的分子的平动动能之和 第 5 节 玻耳兹曼分布律 一、重力场中粒子按高度的分布 大气,平衡态,温度 T PV= RT 不成立 h dh P dP ,n dn P nkT 成立 h P,n dP gdh (1) :空气质量密度 nm ,m: 空气分子质量 P0 , 0 n dP kTdn (2) kTdn gdh nmgdh dh , kT mg n n dn h n 0 0 kT mgh n n 0 ln RT gh kT mgh n n e n e 0 0 h ,n RT :等温气压公式 gh kT mgh kT mgh P nkT n kTe P e P e 0 0 0 h , P 高度计 例:求大气中 n 相差一倍的两处的高度差 已知:空气 kg ,T=300K 3 28.97 10 解:h1 处, RT , 处, gh n n e 1 1 0 h2 RT gh n n e 2 2 0 h2 > h1 , = , RT g h h e n n ( ) 1 2 2 1 2 1 ln 2 ( ) 2 1 RT g h h m g RT h h 3 2 1 6.10 10 ln 2 二、玻耳兹曼分布率 n , kT mgh n n e 0 kT P n n e 0 n0 T (适用于任意的保守力场) T T :分子势能 P T :势能零点处的分子数密度 n0 P P ,n ;T ,n ;T ,n n0

分子热运动有使分子趋向均匀分布的趋势 外力场有使分子聚集在势能较低处的趋势 两者的共同作用使气体分子形成了一种平衡的非均匀分布 dN=nadp=n,e若dxdyd= 玻耳兹曼分布律:气体分子按空间位置的分布规律
5 分子热运动有使分子趋向均匀分布的趋势 外力场有使分子聚集在势能较低处的趋势 两者的共同作用使气体分子形成了一种平衡的非均匀分布 dN ndV n e dxdydz kT P 0 玻耳兹曼分布律:气体分子按空间位置的分布规律