西安电子科技大学：《大学物理》课程教学讲义（下）10-7 导体

静电场中的导体和电介质 第1节静电场中的导体 一、导体的静电平衡条件 1、导体的结构 金属导体=金属正离子+自由电子，自由电荷 2、静电感应和静电平衡 感生电荷 导体B 静电平衡状态 3、导体的静电平衡条件 E=E4+EB,EB内=E4+EB B内任一自由电子，F=eE呐=0 E躺=0 导体内部不能有电力线存在 推论：（1)导体是一个等势体，导体表面是一个等势面 (2)E表面⊥导体表面 证明： (1)Up-Ue =Ei0, Up=Uo (2)电力线与等势面处处正交 二、导体上的电荷分布 1、导体内无净电荷，电荷只分布在导体表面上 证明：反证法，设导体内有 一未被抵消的净电荷9 E:5=g/6≠0 一S上E不能处处为零，与静电平衡条件矛盾 2、导体表面附近的E B E.n E.ds=fE cosas, -E cosas+Ecosais, +JEcos@dS=EAS=OAS E=0 E=， 龙=口元 导体 80 80 (1)只适用于导体表面附近

1 静电场中的导体和电介质 第 1 节 静电场中的导体 一、导体的静电平衡条件 1、导体的结构 金属导体=金属正离子+自由电子，自由电荷 2、静电感应和静电平衡 感生电荷 A 导体 B 静电平衡状态 3、导体的静电平衡条件 E EA EB ，      EB EA EB    内   B 内任一自由电子，  内  0 EB F e   内  0 EB 导体内部不能有电力线存在 推论：（1）导体是一个等势体，导体表面是一个等势面 （2） E表面导体表面  证明：（1） UP UQ P Q = =0，   Q P E dl   Q UP  UQ P P E  （2）电力线与等势面处处正交 二、导体上的电荷分布 1、导体内无净电荷，电荷只分布在导体表面上 证明：反证法，设导体内有 一未被抵消的净电荷 q0 q0 / 0   0 0   E dS q  S   S  S 上 E 不能处处为零，与静电平衡条件矛盾  2、导体表面附近的 E  B E  n  = ，   S E dS   S EcosdS A S = + ， 侧 E cosdS 上 E cosdS  + = ， =0 下 EcosdS 0   S E S    E  n0  ， 导体 0   E  0 0 E n      （1）只适用于导体表面附近 Q

(2)Exo (3)E是所有电荷产生的 3、表面曲率对电荷分布的影响 尖端放电 孤立导体 表面曲率大（凸而尖），σ大 表面曲率小（平坦），σ小 凹的地方， σ更小 尖端处，σ较大，E较大 E>空气击穿场强，尖端放电 三、导体壳（腔内无带电体） 导体腔 (1)内表面上无净电荷，电荷只分布在外表面上 (2)腔内无电场，腔内处处等电势且等于导体壳的电势 证明：（1) fE=0,→∑9，=0 内表面上电荷代数和为零 ()内表面不带电，原命题得证 ()内表面带等量异号电荷X 反证法： Up-U。=∫E.i>0,Up>Uo,矛盾 (2)腔内E处处为零 腔内处处等电势且等于导体壳的电势 四、导体壳（腔内有带电体) 1、导体壳内表面上电荷与 腔内带电体上电荷代数 和为零 证明：fE=0 →∑9：=0 q 9+Q

2 （2） E   （3） E 是所有电荷产生的  3、表面曲率对电荷分布的影响 尖端放电 孤立导体 表面曲率大（凸而尖）， 大 表面曲率小（平坦），  小 凹的地方，  更小 尖端处， 较大， E 较大 E  空气击穿场强，尖端放电 三、导体壳（腔内无带电体） 导体腔 （1）内表面上无净电荷，电荷只分布在外表面上 （2）腔内无电场，腔内处处等电势且等于导体壳的电势 证明：（1） S Q P    0 ， S E dS      0 内 i q 内表面上电荷代数和为零 （i）内表面不带电，原命题得证 （ii）内表面带等量异号电荷 反证法：      0， ，矛盾 Q P P Q U U E dl   UP  UQ （2）腔内 E 处处为零  腔内处处等电势且等于导体壳的电势 四、导体壳（腔内有带电体） 1、导体壳内表面上电荷与 腔内带电体上电荷代数 和为零 证明：   0 S E dS   S    0 内 i q q q  Q

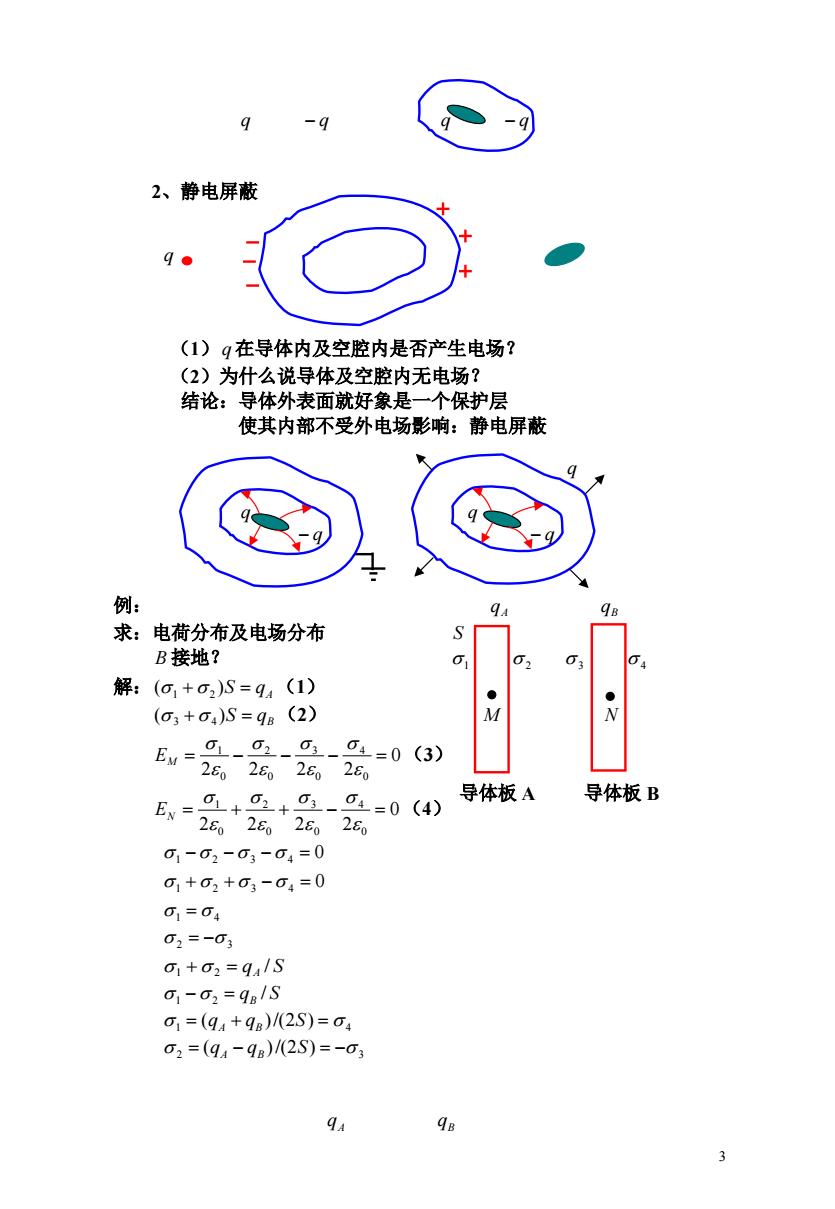
q -9 2、静电屏蔽 q● (1)q在导体内及空腔内是否产生电场？ (2)为什么说导体及空腔内无电场？ 结论：导体外表面就好象是一个保护层 使其内部不受外电场影响：静电屏蔽 9 例： q 求：电荷分布及电场分布 S B接地？ 0 03 解： (o1+02)S=94 (1) ● (o3+04)S=9B (2) M Eu=0-g-a1- 04=0(3) 2602626 280 E,=g++-g=04 导体板A 导体板B 28262626 01-02-03-04=0 01+02+03-04=0 01=04 02=-03 o1+02=q4/S o1-02=9B/S o1=(94+9B)/2S)=o4 o2=(94-9B)/(2S)=-03 ga 98 3

3 q  q q  q 2、静电屏蔽 q （1）q 在导体内及空腔内是否产生电场？ （2）为什么说导体及空腔内无电场？ 结论：导体外表面就好象是一个保护层 使其内部不受外电场影响：静电屏蔽 q q q  q  q 例： qA qB 求：电荷分布及电场分布 S B 接地？ 1  2  3  4 解：(1  2 )S  qA （1） （2） B (  )S  q  3  4 M N 0 （3） 2 2 2 2 0 4 0 3 0 2 0 1              EM 0 （4） 2 2 2 2 0 4 0 3 0 2 0 1              EN 0 1  2  3  4  0 1  2  3  4  1   4  2   3 1  2  qA / S 1  2  qB / S 1 4   (qA  qB )/(2S)   2 3   (qA  qB )/(2S)   qA qB 导体板 A 导体板 B

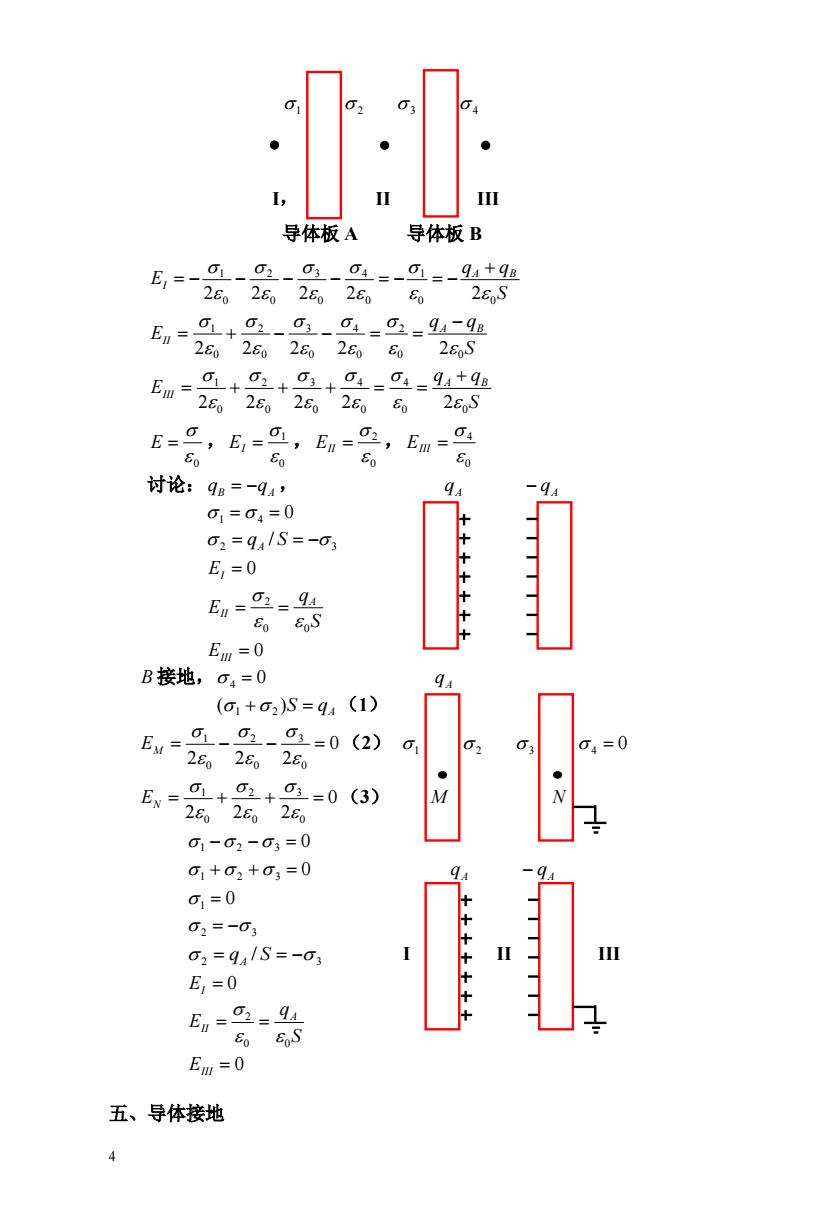
03 I 导体板A 导体板B 品爱品品号 28S E=%+g-93-0-42-91- 2828228628S Em=9+92++0--94+9a 282'28,286026,S E=- ,E1 1,Em= 04 o 02,Em= 8 60 讨论：9B=-94, 01=04=0 02=941S=-03 E,=0 En=2=94 8,6S Em=0 B接地，O4=0 GA (o1+o2)S=q4 (1) Eu=g-92- 01=0(2) 04=0 26026260 ● 6-爱+2+爱=0o) 2e0 01-02-03=0 01+02+03=0 01=0 十+ 02=-03 02=94/S=-03 E,=0 En-0=94 0 EoS Em=0 五、导体接地 4

4 1  2  3  4 I， II III S q q E A B I 0 0 1 0 4 0 3 0 2 0 1 2 2 2 2  2                    S q q E A B II 0 0 2 0 4 0 3 0 2 0 1 2 2 2 2  2                 S q q E A B III 0 0 4 0 4 0 3 0 2 0 1 2 2 2 2  2                 ， ， ， 0   E  0 1   EI  0 2   EII  0 4   EIII  讨论： ， qB  qA qA  qA 1   4  0 2 3   qA / S   EI  0 S q E A II 0 0 2      EIII  0 B 接地， 0  4  qA (1  2 )S  qA （1） 0（2） 2 2 2 0 3 0 2 0 1           EM 1  2  3  4  0 0（3） 2 2 2 0 3 0 2 0 1           EN M N 0 1  2  3  0 1  2  3  qA  qA 1  0  2   3 I II III 2 3   qA / S    0 EI S q E A II 0 0 2      EIII  0 五、导体接地 导体板 A 导体板 B

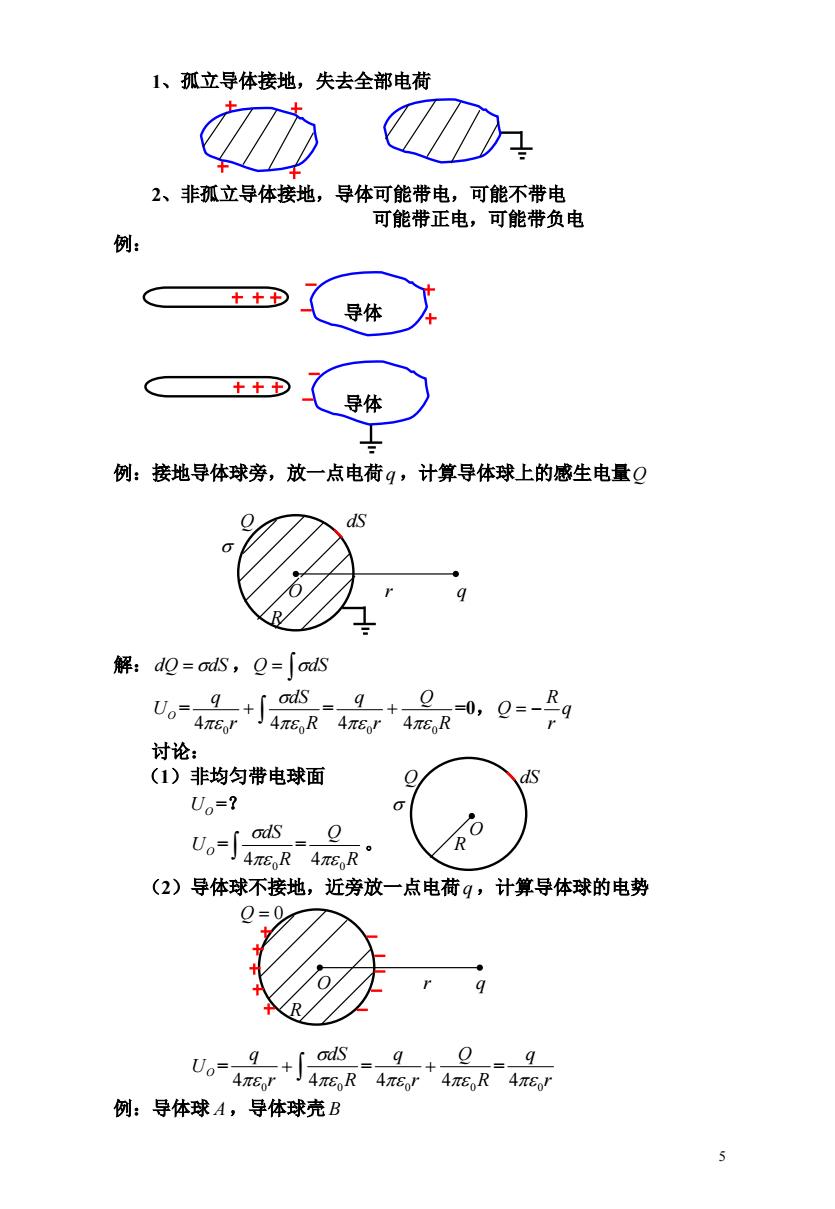
1、孤立导体接地，失去全部电荷 2、非孤立导体接地，导体可能带电，可能不带电 可能带正电，可能带负电 例： 导体 导体 例：接地导体球旁，放一点电荷g,计算导体球上的感生电量Q ds 解：dQ=odS,Q=「odS U。产4 9+0,Q=-g 9=+]4mER4π6r4nED 讨论： (1)非均匀带电球面 Uo=? 6 Uo-∫R4R (2)导体球不接地，近旁放一点电荷q,计算导体球的电势 Q=0 U。=4E+J4ER4E4E,R4E 例：导体球A,导体球壳B

5 1、孤立导体接地，失去全部电荷 2、非孤立导体接地，导体可能带电，可能不带电 可能带正电，可能带负电 例： 导体 导体 例：接地导体球旁，放一点电荷q ，计算导体球上的感生电量Q Q dS  O r q R 解：dQ  dS ，  Q  dS UO =   = =0， R dS r q 4 0 4 0    R Q r q 4 0 4 0    q r R Q   讨论： （1）非均匀带电球面 Q dS =？ UO  = = 。 UO  R dS 4 0   R Q 4 0  R （2）导体球不接地，近旁放一点电荷q ，计算导体球的电势 Q  0 O r q R UO = = =   R dS r q 4 0 4 0    R Q r q 4 0 4 0    r q 4 0  例：导体球 A，导体球壳 B O