
一、 选择题(10小题,每小题3分,共30分) 1、一电动小车从静止开始在光滑的直线轨道上行驶。若小车的电动机的功率恒定, 那么它所走的路程3与时间t的关系如何() A、Sct B、Sct2 c、s2ct D、s2cf3 2、一质点沿半径为R的圆周按规律5=加-c?运动,其中b、c是正的紫量。在 切向加速度与法向加速度的大小相等时,质点运动速度的大小为( ) A、V2CR B、VCR c、 b2 bR b2 bR d2Vc D、 一十 c 2Vc 3、在S制中,一些物理量的量纲如不,其中冲量的量纲为( A、MLT-l B、MLT2 C、ML2T-J D、ML2T-2 4、一力学系统由两个质点组成,它们之间只有引力作用。若两质点所受外力的矢量 和为零,由此可知系统( )。 A、:动量和机械能都守恒 B、动量和机械能都不守恒 C、 动量守恒,但机械能是否守恒不能断定 D、 机械能守恒,但动量是否守恒不能断定 5、地球的质量为m,太阳的质量为M,地心对太阳中心的距离为R,引力常数为G, 地球绕太阳转动的轨道角动量大小为( A、mGMR B、√GMm/R C、MmVG/RD、√GMm/2R 6、如图所示,在水平光滑的圆盘上,有一质量为m的质点,拴在一根穿过圆盘中心 光滑小孔的轻绳上。开始时质点离中心的距离为”,并以角速度⊙转动。今以均匀 速度向下拉绳,将质点拉至离中心r/2处时,拉力所作的功为( A、 1 B、 C、 F > D、 r202 2

7、倔强系数分别为k和k,的两根弹簧,按图所示的三种方式与物体组成振动系统。 如果不计摩擦,那么它们的周期的关系应是( ) A、T=T3≠T B、T=T≠T C、T=T3=T D、T≠T2≠T 振动系统1 振动系统2 振动系统3 8、由图所给的波形图和P处质元振动图,可得该简谐波方程为( C、y=0.02cos 2 D、条件不足不能确定 y(m) y(m) 0.02 0 x(m) 0 0.2 t(s) (a)-0时波形图 (b)P处质元振动图 9、如图所示,S,,为两平面波波源,它们的振动方程分别为y=0.3c0s(2+)cm, 和y2=0.4c0s(2πt+π)cm,它们发出的波在P点 相遇而迭加,图中r=40cm,72=45cm.如图两波 波速都为v=20cm·s,那么两波在P点叠加后的 合振幅为( A、0.1cmB、0.5cm C、0.7cmtD、以上情况都不是 S2 10、关于功和能量的概念,以下说法中正确的是( A、保守力作正功,系统内相应的势能增加 B、作用力和反作用力大小相等方向相反,所以二者作功的代数和必为零 C、质点运动经一闭合路径回到初始点,则保守力对质点作的功为零 D、质点运动经一闭合路径回到初始点,则系统的机械能守恒 应存海滑(产

,淡数味两”过式做会驱杀君型, 二、填空题(10小题,每小题3分,共30分)别 表醉破不果测 1、质量为m的物体,在力F=-0mx作用下沿x轴运动,其中0为正的常系数。 己知在t=0时,质点在x。=A处,且速度。=0,则此物体的运动速度的表达式为 V= ,物体的运动方程为x= 2、一质量为M的质点沿x轴正向运动,假设该质点通过坐标为x时的速度大小为 心(k为正常量),则此时作用于该质点上的力F= ,该质点从 x=x,点出发运动到x=x,处所经历的时间△1= 3、如图所示,质量为m的质点,在竖直平面内作半径为r、速率为v的匀速圆周运 动,在由点A运动到点B的过程中,所受合外力的冲量为= ;除重力以 外,其它外力对物体所做的功为W= B 《这位清在是两女满心,,4置 +元拉1=r明 4、已知质点在F=2i+3j处受到外力F=ti+t2(SI),求第2秒末的该力相对于 。 原点的力矩M= 5、如图所示,一根长I,质量为m的匀质细棒可绕通过点0的水平光滑轴在竖直平 面内转动,则棒的转动惯量I= 品;当棒由水平位置静止释放转 动到图示的位置时,则其角速度0= 1/3 7的生行你卧达 6、一长为1,质量均匀的链条,放在光滑的水平桌面上,若使其长度的/2悬于桌 边下,然后由静止释放,任其滑动,则链条全部离开桌面时的速率为
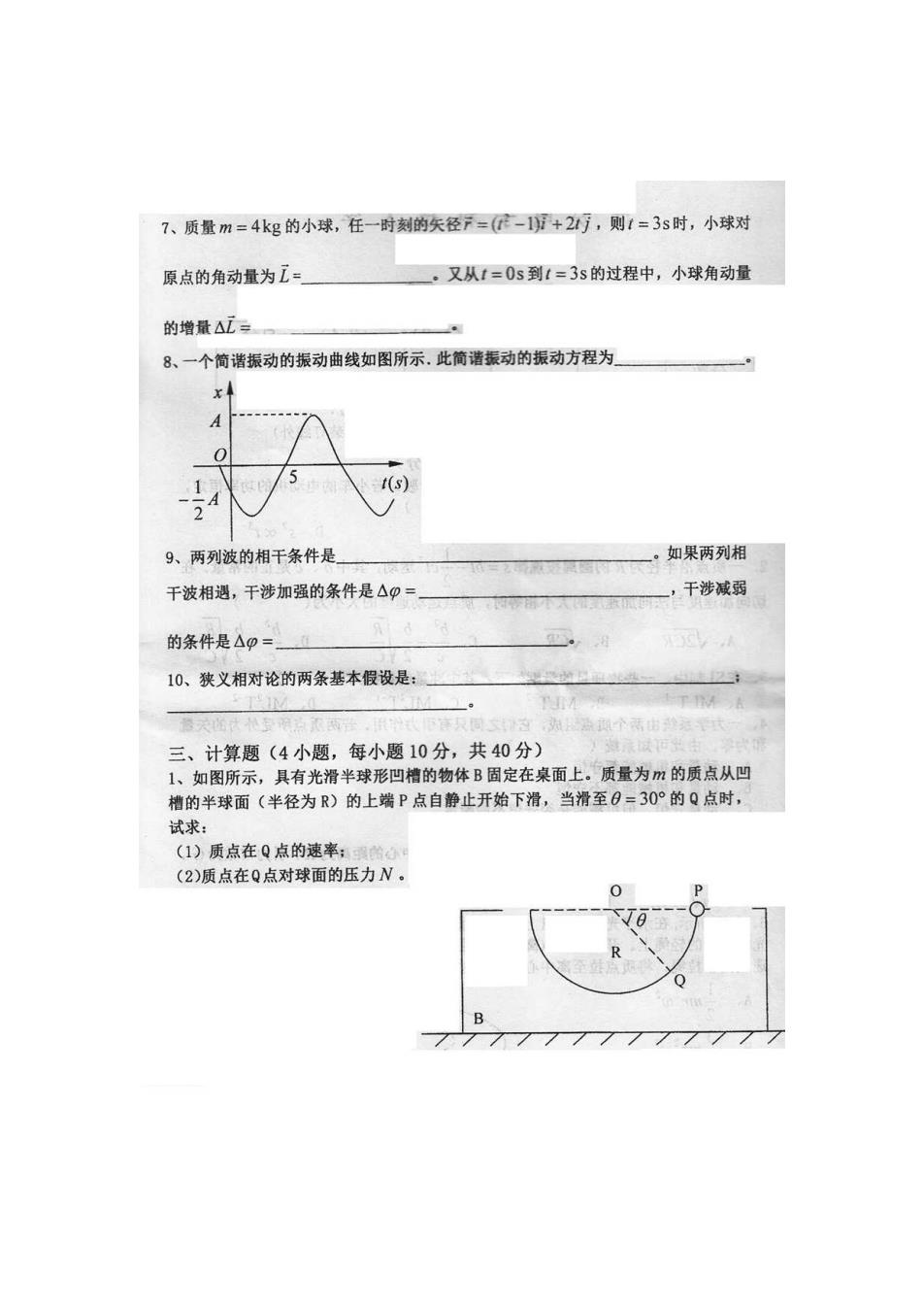
7、质量m=4kg的小球,任一时刻的矢径F=-1)+21万,则1=3s时,小球对 原点的角动量为= 又从1=0s到t=3s的过程中,小球角动量 的增量△L= 8、一个简谐振动的振动曲线如图所示.此简谐振动的振动方程为 9、两列波的相干条件是 如果两列相 干波相遇,干涉加强的条件是△0= 干涉减弱 的条件是△p= 。 10、狭义相对论的两条基本假设是: 山2; T1 三、计算题(4小题,每小题10分,共40分) 1、如图所示,具有光滑半球形凹槽的物体B固定在桌面上。质量为m的质点从凹 槽的半球面(半径为R)的上端P点自静止开始下滑,当滑至O=30°的Q点时, 试求: (1)质点在Q点的速率:喻 (2)质点在Q点对球面的压力N。 0 R
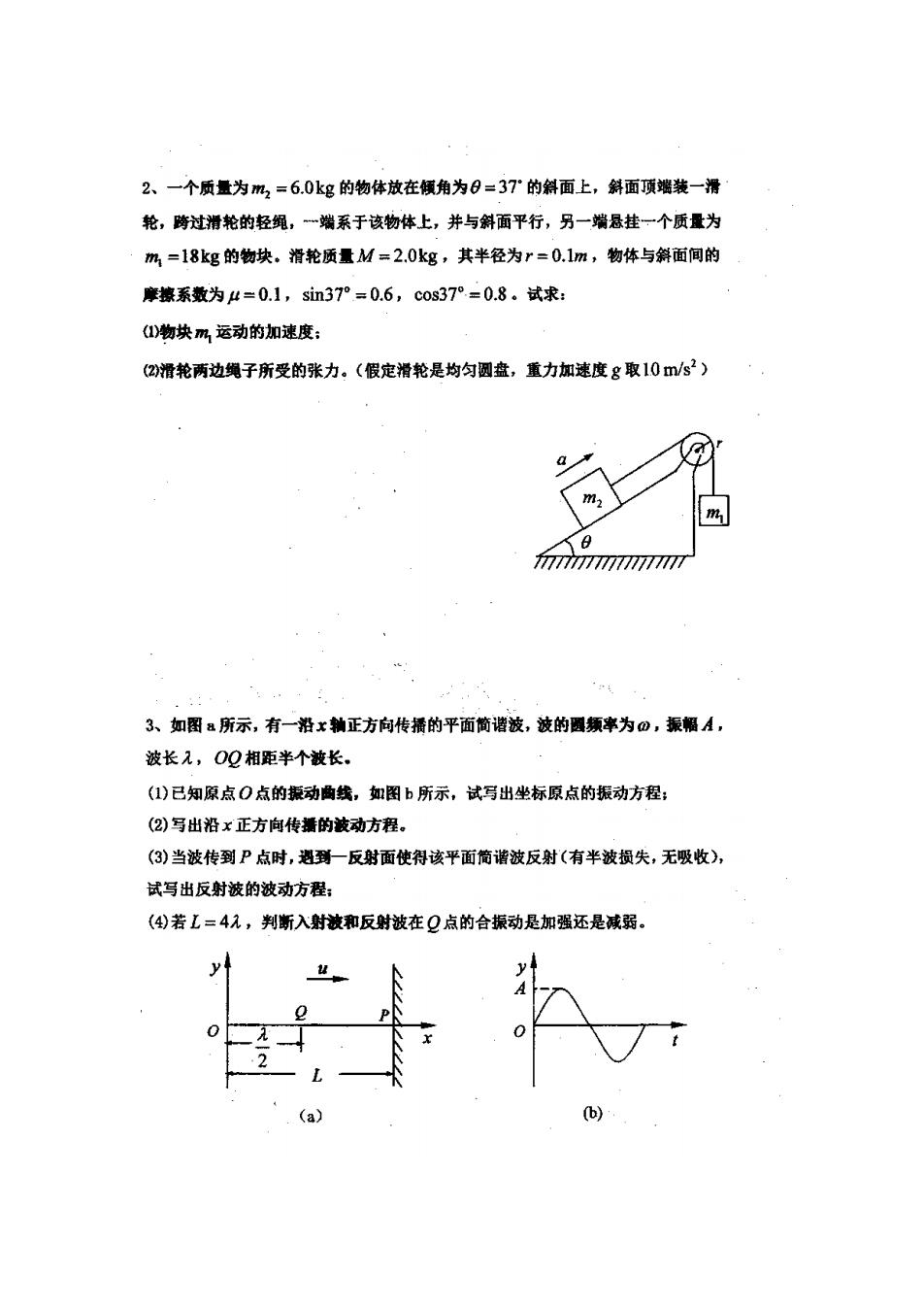
2、一个质量为m2=6.0kg的物体放在倾角为日=37”的斜面上,斜面项端装一滑 轮,跨过滑轮的轻绳,一端系于该物体上,并与斜面平行,另一端悬挂一个质量为 m1=18kg的物块。滑轮质量M=2.0kg,其半径为r=0.1m,物体与斜面间的 摩擦系数为4=0.1,sin37°=0.6,cos37°=0.8。试求: 1)物块m运动的加速度: (2滑轮两边绳子所受的张力。(假定滑轮是均匀圆盘,重力加速度g取10/s2) a m, imm7mn77m 3、如图a所示,有一沿x轴正方向传播的平面简谐波,波的圆频率为0,振幅A, 波长入,O2相距半个被长. (1)已知原点O点的振动胸线,如图b所示,试写出坐标原点的振动方程: (2)写出沿x正方向传播的波动方程。 (3)当波传到P点时,遇到一反射面使得该平面简谐波反射(有半波损失,无吸收), 试写出反射波的波动方程: (4)若L=4入,判断入射波和反射波在Q点的合振动是加强还是减弱。 (b)

4、北京至上海的距离为1463细,甲乙两列火车分别从北京和上海站相向开出,已知乙 车比甲车晚开3.5×103s。今有-一宇由飞船以0.9c的速度从北京至上海的上空飞过。 试求飞船上的宇航员测得两列火车发车的时博楚,若北京站另一列开往上海方向的丙火 车发车时间比甲车也晚3.5×10~3s,则字航员测得甲丙两列火车的发车的时间差又是多 少?

一、选择题(10小题,共30分) 1.D 2.B 3.A4.C5.A6.B7.A8.B 9.c10.c 二、填空题(10小题,共30分) 1.odcos(er+-mdsin(ot) x=4sin(om+2=4cos(a个 2.Mk'x, 2晚 3.i=mi+m网,p=m2-m2+mg)=-g 4.2k N.m 515n =3gsine/1 6.√3g14 7.-80kgm2/s,-72kgm2/3 &0=o+ 9.频率相同、振动方向相同、位相差恒定,△0=2m,k=0,士1,士2, △p=(2k+1)m,k=0,1,2, 10.狭义相对性原理,光速不变原理
丶 忄∷ ← 丶 一 ℃ 三 廴 ˇ 二 ∷ ⒈ T邕|罗塄∷F∶∴:∶ ∷土:∷ ∶ '∴ ∷∴∷⒏∶ 磕盛趱i击永巅|垂击奋|∷ ∷|∷|∶ ∷∷∷△|∷| 。·0而=7二 ″ 灬t″ ∷ |拿△〃哪叨? △砷枣||争|Ⅱ纹Ⅱ |ⅡⅡ∷∷ Ⅱ △¨ ∷ ∴ ∷- ∷ 诲∷ ∷∷ ∷ ∷ ∷∴∷|∶ Ⅲ|∷ ”吨| |动∷⊥Ⅱ ⒋ 2kN· m ||告冫 '∷ ∷ ←腼 ∷∷∷∷ 9,C 10∶ C `亠 Ⅰ =∷

三、计算题(4小题,共40分) 1、解(1)用牛顿定律求解: "RQ 法向:N-mg sin0=m (各2分) 切向:mg cos0=m 由(2)得 gcose=业-dv dsdv =V dt ds dr ds vdv=gcos ads=g coseRde vdv-gRcos@i0-gRsin0 v2 =gRsin0→v=√2 gRsin6→v=√gR 2 (2分) (2)用机械能守恒定理求解: 取凹槽最低点为重力势能零点,则有: mgR=m'+mg((R-Rsin)-→v=2 gRsin9 (4分) 2 (2)由式(1)得 v N=mgsin+m =mg sin+m 2gRsin0 (2分) R R N=3mg sin (2分) 当0=30时N=3mg=15mg 2 (2分) 2、解:分别对物块m和m2以及滑轮列动力学方程 m8-T=m,a(2分) T3-m2gsin37°-m2gcos37°=m2a (2分) (G-Ty=IB=1M'B (2分) 其中rB=a (1分) 2 得到a="m8-m8sin37°-m28cos37 =5.568(m/s2) (1分) M+%+m% 1 T=m,(g-a)=79.776N (1分) T2=m2gsin37°+m2gcos37°+m2a=74.208N (1分)
·冖鹳 ˉⅡ_ ∷ Θ 一 〓∷∷ ∷ dν ν 一峦 〓 一 1丶 ∷ · (各 2分) |∷ |=亠:_∷ (2乡〉) (2彡卜) 畔∵△?△若 艹 虹h夕 →v=√2型 sh夕 →v〓 枷 (2)用 机械能守恒定理求解: 取凹槽最低点为重力势能零点,则有: ∶∫∶女∷i召 =0Ir呷柙 ° 氵 ·胛 田 ∵ ~ Ⅳ 〓3刀gsh汐 当夕=30° 时Ⅳ=:绍 =l· 5砣 艋艹菽土导箨麇鳏珲钅毳ξ皙岑T芏蕊綦鎏△∷ ¨ 勿lgˉ 石=啊I曰 【2分 ) |ˉ 马ˉ〃2gsh37° -/Fm2gcos37° =〃2曰 (2分) (⒒ -马 )r· 昭 =:″卩 ' (2分 ) 其中F'=曰 ∷ (0分 ) 虫Ⅱ∷ -艹PF 冖 F叩 内 叩 ¨ 石△吧臼∷Θ=’⒍,TcNˉ々i砻辶·¨Ⅱ∷∷ ∷ 梦) (2分 ) (2彡卜) 石了| 马〓抑2g⒍n37° +/Fm2gcos37° +仞2夕 △74.208N (1分 )

3、解0%=4coa-孕 (2分) 2元 ⑦y=Acos(aot- (2分) ③P点反射后的振动方程y。=Acos(ot 2TL-元±)(士π表示半波损失)(2分) 反射波的波动方程 %=4u-受-经u--对=aar受aL--± (2分) 、 ④△p=4π -士元=4机元 2土元=14元±π= 15π (2分) 13元 满足减弱条件,是减弱的(即该点不振动)。· 4、解: 取地面为S系,飞船为S'系,以北京为S系的原点,北京至上海方向为x(x')轴正向,如图 所示。对甲乙两列车,△11=3.5×103s,△x=1.463×10m (2分) 由时空间隔变换关系式有 △= 4 3x108×1.463x106 3.5×103-0.9 -=-2.04×103(S0 (2分) -总 v1-0.92 表明飞船中的宇航员测得丙车仍然是晚于甲车发车,两参照系的时序不变。 0.9c 0 北京 上海xx')
∵∵∶∷∵T∶∵∵鳕 3、 解①yO丁 Z。os(烫″-:), 。9≡ 彳ooso泌 -2翌 J-号 ;)· ③P点反射后的振动方程y、 〓/cos(仞 -箐£-:± 冗)(± 冗奉示半波损失) (2分) 反射波的波动方程 yFx=/cos[臼矽-2工 L-旦王(£ ~r)~:± 冗]〓 彳CosIJ9r-旦工(2£ ~x)~:± π]. (2钥卜) °个访=4冗 ≡⊥△生±冗=4冗 兰∠二∶全±冗=.4π ⊥冗〓 {l:1 满足减弱条件,是减弱的 (即 该点不振动)。 , (2分 ) (2分 ) 4、 解: 取地面为s系∷Ⅱ飞船为s′ ∷系△以北京为 s系 的原点,北京至上海方向为豸(/)轴 正向,如 图 所示。对甲乙两列车,Δ九=3· 5× 10· s,加l=1.463× 1俨 勿 由时空间隔变换关系式有 (2分 ) (2分 ) 〓-2。 04× 10丬 (s)(0 (4.兮 ) ˇ辶θ亻下) Δ∫丨= Δ莎l-∠ ±AFl ~3.5× I?ˉ 3-了∮:1F× 1· 463I106 ∴∥ψ ˉ 讷工W // ェ 矿 Wθ 表明在飞船中的宇航员测得北京站的甲车晚于上海站的乙车2。 04× 10ˉ 3(s)发 车,时序发生 了颠倒。 对甲丙两列火车,ΔJ2=Δ气=3.5× 1σ3s,扭2=0 于 是 Δ呓=-Π=尘些±亠F〓 3· 5k10ˉ3=:.03× 10ˉ 3(s)>0 (2.兮 ) 亻t1Ⅰ亏,了 ^岬 表明飞船中的宇航员测得丙车仍然是晚于甲车发车,两 参照系的时序不变。 (2.兮 ) 土丁llIdη ︱丨l扯 丫 宀只 丬 LL 丬 l~(丝)2 C 止海 Ⅳ FⅣ fj