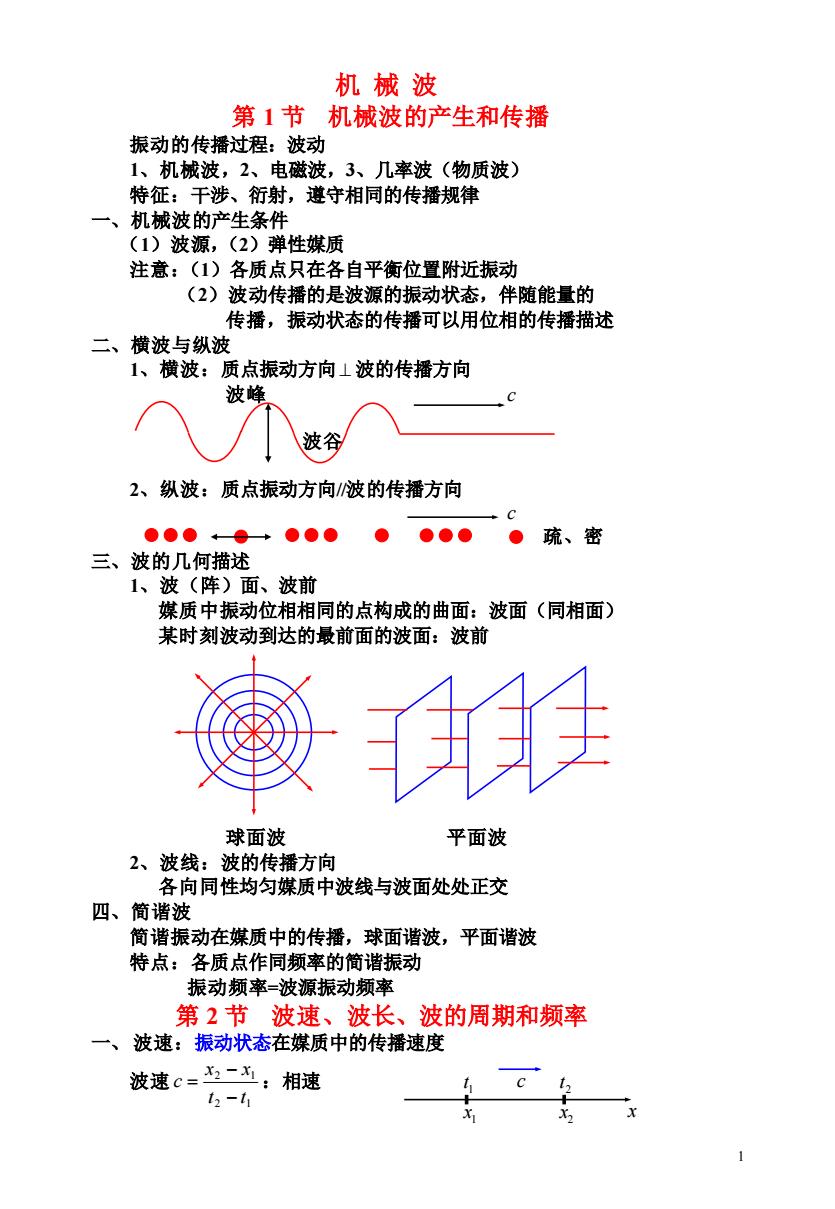
机械波 第1节 机械波的产生和传播 振动的传播过程:波动 1、机械波,2、电磁波,3、几率波(物质波) 特征:干涉、衍射,遵守相同的传播规律 一、机械波的产生条件 (1)波源,(2)弹性媒质 注意:(1)各质点只在各自平衡位置附近振动 (2)波动传播的是波源的振动状态,伴随能量的 传播,振动状态的传播可以用位相的传播描述 二、横波与纵波 1、横波:质点振动方向⊥波的传播方向 波蜂 波谷 2、纵波:质点振动方向波的传播方向 ●●●←●+●● ●●●●● 疏、密 三、波的几何描述 1、波(阵)面、波前 媒质中振动位相相同的点构成的曲面:波面(同相面) 某时刻波动到达的最前面的波面:波前 球面波 平面波 2、波线:波的传播方向 各向同性均匀媒质中波线与波面处处正交 四、简谐波 简谐振动在媒质中的传播,球面谐波,平面谐波 特点:各质点作同频率的简谐振动 振动频率-波源振动频率 第2节波速、波长、波的周期和频率 一、波速:振动状态在媒质中的传播速度 波速c=-士:相速 t2-t1 1
1 机 械 波 第 1 节 机械波的产生和传播 振动的传播过程:波动 1、机械波,2、电磁波,3、几率波(物质波) 特征:干涉、衍射,遵守相同的传播规律 一、机械波的产生条件 (1)波源,(2)弹性媒质 注意:(1)各质点只在各自平衡位置附近振动 (2)波动传播的是波源的振动状态,伴随能量的 传播,振动状态的传播可以用位相的传播描述 二、横波与纵波 1、横波:质点振动方向 ⊥ 波的传播方向 波峰 c 波谷 2、纵波:质点振动方向//波的传播方向 c 疏、密 三、波的几何描述 1、波(阵)面、波前 媒质中振动位相相同的点构成的曲面:波面(同相面) 某时刻波动到达的最前面的波面:波前 球面波 平面波 2、波线:波的传播方向 各向同性均匀媒质中波线与波面处处正交 四、简谐波 简谐振动在媒质中的传播,球面谐波,平面谐波 特点:各质点作同频率的简谐振动 振动频率=波源振动频率 第 2 节 波速、波长、波的周期和频率 一、 波速:振动状态在媒质中的传播速度 波速 2 1 2 1 t t x x c − − = :相速 1 t c 2 t 1 x 2 x x

弹性 波速仅由媒质的特性决定 惯性 1、液体和气体内部纵波c=√B/pB:体变弹性模量p:密度 2、固体内部 横波c=√G引pG:切变弹性模量 纵波c=YIP Y:杨氏弹性模量 3、绳子或弦线上横波c=√T14T:张力μ:质量线密度 二、波长、波的周期和频率 同一波线上振动位相差为2π 的两点间的距离:波长入 一个波通过波线上某点所需要 的时间:波的周期T 入:空间上的周期性,T:时间上的周期性 波的周期=波源的振动周期 波的频率v=】-波源的振动频率 o=2πv:波的圆频率 三、C,,v的关系:c=子=v 注意:1、波速由媒质决定,v由波源决定,入由两者决定 2、V弹性媒质,彐频率上限 第3节 波动方程(波函数) 一、平面谐波的波动方程 yo Acos(ot+) x处质点的振动滞后于 O点处质点,△t=x/c x处质点1时刻的振动状态 与O点处质点t-△t时刻的振动状态相同 y(x,)=yot-△)=AcosI@(t-△)+p]=Acos[ot-)+p] yx,)=Acos[ot-)+p]一一波动方程(波函数) 二、波函数的物理意义 1、x、1给定,给出x处质点1时刻的振动位移 2、x给定,给出x处质点的振动方程 3、1给定,给出x轴上各质点的振动位移 方程代表1时刻的波形曲线方程 2
2 波速仅由媒质的特性决定 惯性 弹性 1、液体和气体内部 纵波 c = B/ B:体变弹性模量 :密度 2、固体内部 横波 c = G/ G:切变弹性模量 纵波 c = Y / Y:杨氏弹性模量 3、绳子或弦线上 横波 c = T / T:张力 :质量线密度 二、波长、波的周期和频率 同一波线上振动位相差为 2 c 的两点间的距离:波长 一个波通过波线上某点所需要 的时间:波的周期 T :空间上的周期性, T :时间上的周期性 波的周期=波源的振动周期 波的频率 T 1 = =波源的振动频率 = 2 :波的圆频率 三、 c, , 的关系: = = T c 注意:1、波速由媒质决定, 由波源决定, 由两者决定 2、 弹性媒质, 频率上限 第 3 节 波动方程(波函数) 一、平面谐波的波动方程 y c y = Acos(t +) O x 处质点的振动滞后于 O x x O 点处质点, t = x / c x 处质点 t 时刻的振动状态 与 O 点处质点 t − t 时刻的振动状态相同 ( , ) = ( − ) = cos[( − ) +] = cos[( − ) +] c x y x t y t t A t t A t O ( , ) = cos[( − ) +] c x y x t A t ——波动方程(波函数) 二、波函数的物理意义 1、 x、 t 给定,给出 x 处质点 t 时刻的振动位移 2、 x 给定,给出 x 处质点的振动方程 y 3、 t 给定,给出 x 轴上各质点的振动位移 t 方程代表 t 时刻的波形曲线方程 x

4、x、1都变化 给出波线上各质点任意时刻的位移 给出波线上各质点的振动方程 1t+△t 给出各个时刻的波形曲线方程 考察时刻x处质点 及t+△r时刻x+c△t处质点 x+c△tx yx.t)=Acos[o(t-)+ol x+cA,1+△)=Acos[ot+△1-x+cA当 )+p]=Acos[o1-)+ y(x,t)=y(x+c△t,t+△t) ΦD(x,)=o(t-)+p D(x+cA,t+△)=ot+△y-x+cA )+p=at-S+9 Φ(x,t)=Φ(x+c△t,t+△t) 波速是整个波形向前推进的速度 注意: 1、x,)=Acos[o1-)+p]=Acos[2π-+p] -Acos[2r(+]Acos[2 (ct-) 2、沿x轴负向传播的平面谐波方程 yo Acos(ot+) x处质点的振动超前于 X O点处质点,△t=x/c x处质点1时刻的振动状态与 O点处质点t+△t时刻的振动状态相同 y(x,)=yot+△)=Acos[@(t+△)+p]=Acos[ot+)+p] x、1两项异号,波沿x轴正向传播 x、t两项同号,波沿x轴负向传播 注意: (1)x处的时刻取为1,(2)△1>0 3、x处质点的振动速度和加速度 y(x.()=Acosto(-)+o V---04sino(-)+] a-亚==-0'4co1-+pl,注意v与c的区别 4、x,)=Acos[o-之+p]对横波、纵波都适用 横波y,V,a⊥x轴,纵波y,V,a∥x轴 3
3 4、 x、 t 都变化 给出波线上各质点任意时刻的位移 给出波线上各质点的振动方程 y t t + t c 给出各个时刻的波形曲线方程 考察 t 时刻 x 处质点 及 t + t 时刻 x + ct 处质点 x x + ct x ( , ) = cos[( − ) +] c x y x t A t ( , ) cos[( ) +] + + + = + − c x c t y x c t t t A t t = cos[( − ) +] c x A t y(x,t) = y(x + ct,t + t) ( , ) = ( − ) + c x x t t + + ( + , + ) = ( + − ) c x c t x c t t t t t =( − ) + c x t (x,t) = (x + ct,t + t) 波速是整个波形向前推进的速度 注意: 1、 ( , ) = cos[( − ) +] c x y x t A t = cos[2 ( − ) +] c x A t = cos[2 ( ) ] − + x T t A = ( ) ] 2 cos[ A ct − x + 2、沿 x 轴负向传播的平面谐波方程 y c y = Acos(t +) O x 处质点的振动超前于 O x x O 点处质点, t = x / c x 处质点 t 时刻的振动状态与 O 点处质点 t + t 时刻的振动状态相同 ( , ) = ( + ) = cos[( + ) +] = cos[( + ) +] c x y x t y t t A t t A t O x、 t 两项异号,波沿 x 轴正向传播 x、 t 两项同号,波沿 x 轴负向传播 注意: (1) x 处的时刻取为 t ,(2) t 0 3、 x 处质点的振动速度和加速度 ( , ) = cos[( − ) +] c x y x t A t , = − sin[( − ) +] = c x A t t y V cos[ ( ) ] 2 2 2 = − − + = = c x A t t y t V a ,注意 V 与 c 的区别 4、 ( , ) = cos[( − ) +] c x y x t A t 对横波、纵波都适用 横波 y ,V ,a ⊥ x轴,纵波 y ,V ,a // x 轴

5、波动微分方程 =-@Acosto(i-)+91=-wy O=Asin[o(t-)+o] &x c 0'y=_o 2Acos[o(t-之)+p]=-2 0y-10y一一沿x轴传播的平面波波动微分方程 Ox2 c2012 三维波动微分方程: a25,a25,a251a25 Ox20y202c2012 (x,y,,),1时刻(x,y,)处质点的位移:波函数 6、同时刻波线上两点位相的比较 y(x.t)=Acos[o(t-)+o] 1 1,x,(x,)=ot-)+p C 1,x2,(x2,)=ot-)+p △Φ=(x2,)-(x,)=-0(x,-x)= 2以 △x=x2-x:波程差, 40=、27 同一时刻沿波的传播方向各质点的振动位相逐点滞后 X2-x1=1,△Φ=-2π 例:已知y。=Acos(1+p) 求:(a)、(b)两种情况下 的波函数 解:(a)x处质点振动滞后于 x处质点,△M=-0 (a) (b) x处质点1时刻的振动状态 与x。处质点t-△t时刻的振动状态相同 y(x.t)=ys (t-At)=Acos[o(t-x-x)+] (b)x处质点振动超前于x,处质点,△M=x- x处质点1时刻的振动状态 与x。处质点t+△1时刻的振动状态相同 y(x.()=yx (t+At)=Acos[o(t+x-x)+o] 4
4 5、波动微分方程 y c x A t t y 2 2 2 2 = − cos[( − ) +] = − sin[( ) ] = − + c x A t x c y y c c x A t x c y 2 2 2 2 2 2 cos[ ( ) ] = − − + = − 2 2 2 2 2 1 t y x c y = ——沿 x 轴传播的平面波波动微分方程 三维波动微分方程: 2 2 2 2 2 2 2 2 2 1 x y z c t = + + (x, y,z,t), t 时刻 (x, y,z) 处质点的位移:波函数 6、同时刻波线上两点位相的比较 ( , ) = cos[( − ) +] c x y x t A t y c t, 1 x , ( , ) =( − ) + 1 1 c x x t t O 1 x 2 x x t, 2 x , ( , ) =( − ) + 2 2 c x x t t = (x2 ,t) −(x1 ,t) = x x x c − − = − 2 ( ) 2 1 2 1 x = x − x :波程差, = − x 2 同一时刻沿波的传播方向各质点的振动位相逐点滞后 x2 − x1 = , = − 2 例:已知 cos( ) 0 yx = A t + y c c y 求:( a )、( b )两种情况下 的波函数 O 0 x x x x x 0 x O 解:( a ) x 处质点振动滞后于 0 x 处质点, c x x t − 0 = ( a ) ( b ) x 处质点 t 时刻的振动状态 与 0 x 处质点 t − t 时刻的振动状态相同 ( , ) ( ) cos[ ( ) ] 0 0 + − = − = − c x x y x t y t t A t x ( b ) x 处质点振动超前于 0 x 处质点, c x x t − 0 = x 处质点 t 时刻的振动状态 与 0 x 处质点 t + t 时刻的振动状态相同 ( , ) ( ) cos[ ( ) ] 0 0 + − = + = + c x x y x t y t t A t x
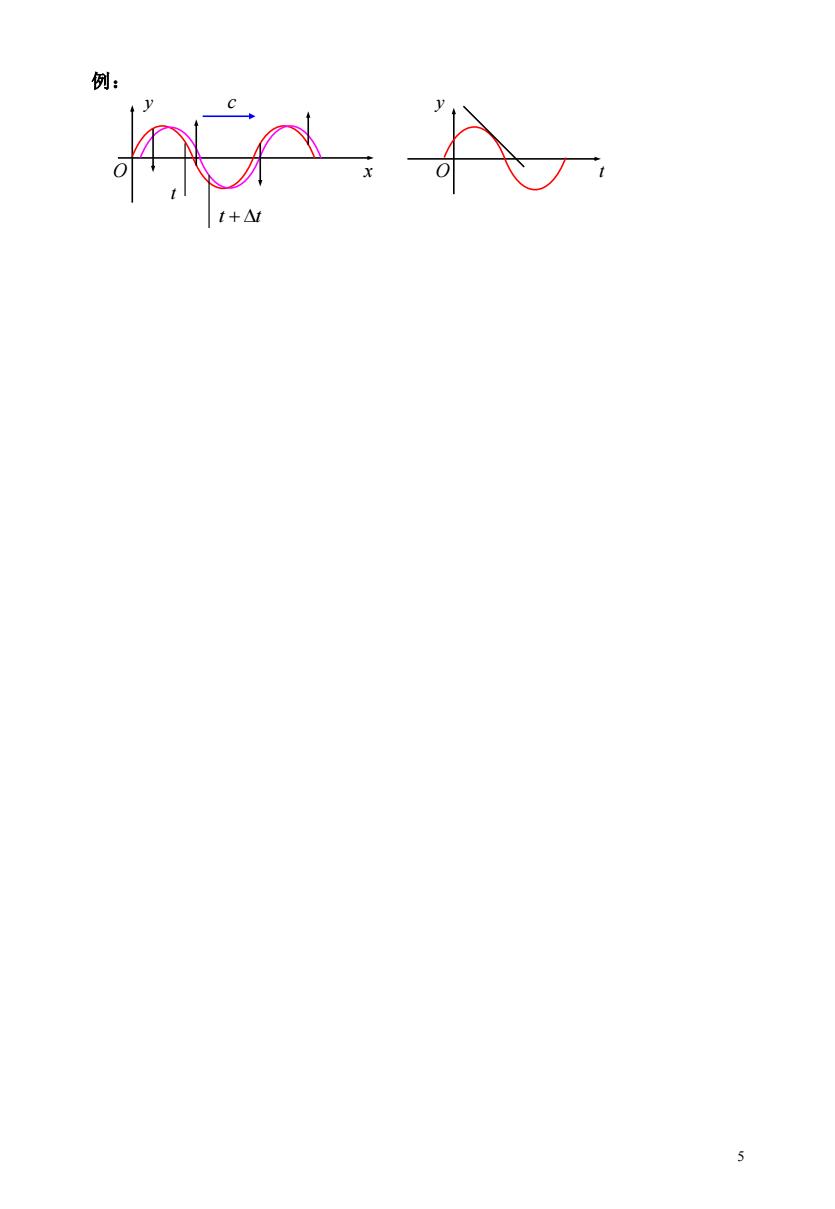
A. 例: 5
5 例: y c y O x O t t t + t