
4.5、衍射光栅 。广义地说,具有周期性的空间结构或者光学性能(透射 率,反射率)的衍射屏,统称为光栅。 透射式 反射式 。光栅种类: 透射光栅和反射光栅;平面光栅和凹面光栅;黑白光 栅和正弦光栅;一维光栅、二维光栅和三维光栅,等 等
4.5、衍射光栅

4.5.1、一维多缝光栅 S 组成:点光源,双透镜,光栅衍射屏,接收屏
4.5.1、一维多缝光栅

。夫琅和费衍射场=单元因子×结构因子 。一维多缝光栅的单元因子 sin a πa sin 0 u(8)∝ a Q= ·结构因子 5= ∑e=1+e8+e2δ+…+ew-18 j=1 δ πdsinθ 令B= 2 λ 则5= sinNBN-1)B sinβ a为缝宽,d为缝间距,1/d称为光栅常数
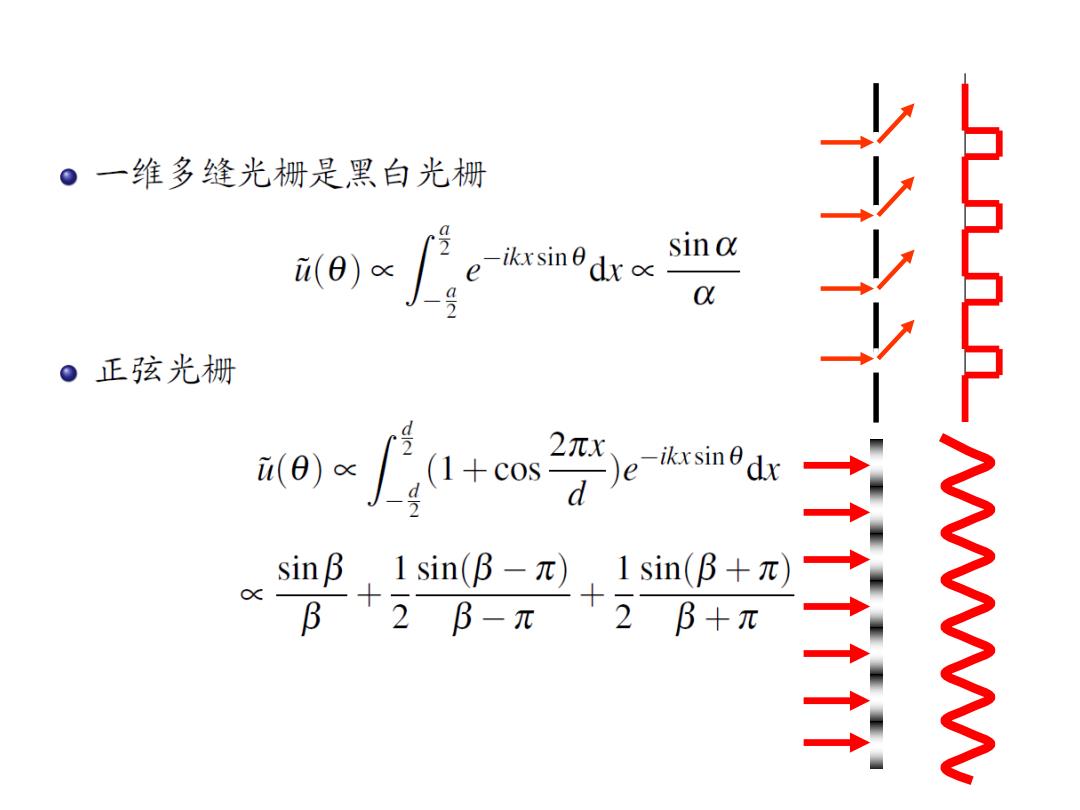
。一维多缝光栅是黑白光栅 sin a x 。正弦光栅 io)/1+coms21etk sinB,1sin(B-π),1sin(B+π) BT2B-π +2B+元 M

。因此一维多缝光栅的衍射强度 1=a-5-0292 sin B 为单缝衍射因子与多缝千涉因子的乘积。 0.6 0.6 0.4 0.2 AAAN△AAAA 0.6

4.5.2、光强分布特点 。多缝干涉因子的影响 (1)主极强的位置与大小 当dsin0=k2,k=0,土1,士2,…时有B=kπ 此时( 大值N单经衍射强度的宿
4.5.2、光强分布特点

方程dsin0k=k入(k=0,士1,士2,…)称为光栅方程。 满足光栅方程的衍射角sin0=k入/d方向将出现主极大,它 的强度是单缝在该方向上的N2倍。(原因?) 主极大的位置与缝数N无关。 主极大的数目有限制 k刘=受sin9≤元 若d<入,除0级外别无主极大

(2)零点位置与主极大半角宽(反映“锐度”)》 Wδ 零点条件:sin2=0而sin2≠0 m、入 sin0=k+R分k=0,士1,士2,…m=1,2,…W-1 每两个主极大之间有(N一1)条暗线,每两条暗线之间有一 个次极大,共有(N-2)个。 主极大半角宽:主极大中心到邻近暗线的距离 A)=aa6=+万月合 入 Nd 入 入 ∴.△6k=Ndcos 0k 偏离中心不远处的主极大△日≈ Nd

·单缝衍射因子的影响 衍射光栅形成的衍射图样称为光栅光谱。光谱的位置 由干涉主极大决定。 单缝衍射并不改变光谱位置,只影响强度在各级光谱 间的分配 0.8

当单缝衍射因子为0时光谱将不再出现,发生缺级现象。 dsin0=k入,asin0=n入,k=0,±1,土2,…;n=土1,±2,… d k .·.缺级满足的方程 一三一 a n 对一块光栅,理论上缺级总存在。而实际上,只有单缝衍 射中央极大区域的谱线才有可观察的强度,考虑衍射第 一 级引起的缺级(即=士1)才有实际意义。因此我们往往只 讨论d/a=整数的情况。 如d/a=3,缺士3级,士6级,士9级·