
例:光滑水平面内,OA⊥OB 1=2m V4=4m/s,'4⊥OA 0 d=OA=0.5m,V⊥OB d=0.5m 求:La=?'B=? m =0.5kg →V4=4mls 解:L4=Lg=m'd=0.5×4×0.5=1kgns Lg=mh,5。==。1 ml0.5×2 =Ims- 例:先使小球做半径为圆周运动,然后 向下拉绳子,使运动半径降为 m 求:(1)此时小球的o1、 60 (2)拉力的功 解:(1)小球对O点角动量守恒 m5=m,=2,=上= 片2 (2)拉力的功 A-AEK=10 2m-) 例:证明m。=a+m(g+a) rATBg-reaa 证明:mBg-TB=mBaB(1) T4-m4g=m4a4(2) TBTE-TATA =JB (3) T aB=TRB (4) a=rB (5) mm(g+a) rArBg-rBaA 例:空心圆环可绕竖直轴AC自由转动 1o@o 转动惯量I。,半径为R,初角速oo 质量为m的小球原来静止于A点 由于微小振动向下滑动,环内壁光 滑,求小球滑到B、C两点时环的 角速度和小球相对环的速度 解:B:1o00=10+mRo→0= 1o0o I。+mR2 1
1 例:光滑水平面内,OA⊥OB = ? VB V m s A = 4 / ,VA⊥OA O B d = OA = 0.5m,VB⊥OB d = 0.5m 求: = ? LB = ? VB m = 0.5kg A V m s A = 4 / 解: LA = LB = mVAd = 2 1 0.5 4 0.5 1 − = kgm s L mV l B = B , 1 1 0.5 2 1 − = = = ms ml L V B B 例:先使小球做半径为 0 r 圆周运动,然后 向下拉绳子,使运动半径降为 1 r 求:(1)此时小球的 1、V1 (2)拉力的功 解:(1)小球对 O 点角动量守恒 0 0 1 1 mV r = mV r , 0 1 0 1 V r r V = , 2 1 0 0 1 1 1 r r V r V = = (2)拉力的功 2 0 2 1 2 1 2 1 A = EK = mV − mV = ( 1) 2 1 2 1 2 2 0 0 − r r mV 例:证明 A B B A A A A A B r r g r a Ja m r g a m 2 2 ( ) − + + = J 证明: mB g −TB = mBaB (1) A r B r TA − mAg = mAaA (2) O TB rB −TA rA = J (3) TA TB aB = rB (4) A a aA = rA (5) A mA mB B B a mAg mBg A B B A A A A A B r r g r a Ja m r g a m 2 2 ( ) − + + = 例:空心圆环可绕竖直轴 AC 自由转动 0 I 0 转动惯量 0 I ,半径为 R ,初角速 0 A 质量为 m 的小球原来静止于 A 点 由于微小振动向下滑动,环内壁光 O B 滑,求小球滑到 B 、C 两点时环的 R 角速度和小球相对环的速度 VC VB 解: B : 2 0 2 0 0 0 0 0 I mR I I I mR + = + = l =2m C 0 r 1 r m O V0
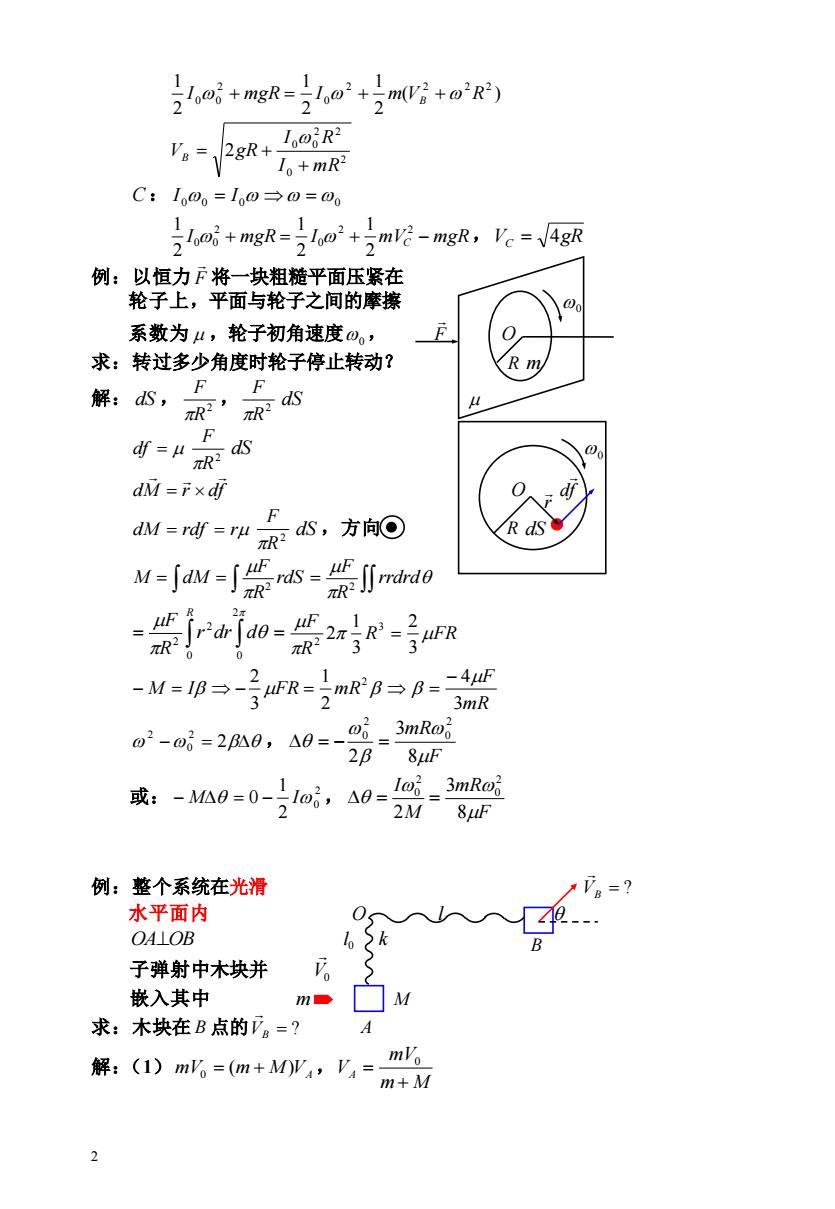
2gR+ 1o@oR2 1o+mR2 C:100=10→0=00 mgRanm-mgk,V.g 例:以恒力F将一块粗糙平面压紧在 轮子上,平面与轮子之间的摩擦 0 系数为4,轮子初角速度。, 求:转过多少角度时轮子停止转动? R m 解:dS, F F TR2, F df=u- -ds πR 00 dM=Fxdf df F M==u放s,方向O da M=j=西= R∫rdrfao=, 2x 22—2xR3—4 -M=B→-R=mRB→B= 3mR -0i-26A0,A0=-0i3mRoi 2B 8uF 或:-M0=0-1o,△9=a=3mRO 2M 8uF 例:整个系统在光滑 VR= 水平面内 OA⊥OB 子弹射中木块并 嵌入其中 M 求:木块在B点的。=? 解:(I)m%=(m+My,y,=m6 m+M
2 ( ) 2 1 2 1 2 1 2 2 2 2 0 2 I 00 + mgR = I + m VB + R 2 0 2 2 0 0 2 I mR I R VB gR + = + C : 00 = 0 =0 I I I + mgR = I + mVC − mgR 2 2 0 2 0 0 2 1 2 1 2 1 ,VC = 4gR 例:以恒力 F 将一块粗糙平面压紧在 轮子上,平面与轮子之间的摩擦 0 系数为 ,轮子初角速度 0, F O 求:转过多少角度时轮子停止转动? R m 解: dS , 2 R F , 2 R F dS df = 2 R F dS 0 dM r df = O df dM = rdf = r 2 R F dS ,方向 R dS = = rdS R F M dM 2 = rrdrd R F 2 = = R r dr d R F 0 2 0 2 2 R FR R F 3 2 3 1 2 3 2 = mR F M I FR mR 3 4 2 1 3 2 2 − − = − = = − = 2 2 0 2 , F mR 8 3 2 2 0 2 0 = − = 或: 2 0 2 1 − M = 0 − I , F mR M I 8 3 2 2 0 2 0 = = 例:整个系统在光滑 = ? VB 水平面内 O l OA⊥OB 0 l k 子弹射中木块并 V0 嵌入其中 m M 求:木块在 B 点的 = ? VB A 解:(1) mV m M VA ( ) 0 = + , m M mV VA + = 0 r B

(2)m+M0r=m+M0+号k-P m%2_k-☒ m+M' m+M (M+m)PAh。=(M+m)Ψlsin sin 0=- mVolo Val -(m+M)k(1-1o) 例:圆盘(m、R)可绕通过其中 心的竖直光滑轴转动,有一人 静止(m=m/10)站在R/2处 m 开始圆盘载人以匀角速®,转动 O R/2 如果此人沿垂直半径方向相对 R 圆盘以速率V作圆周运动,运 动方向与圆盘转动方向相反 求:(1)圆盘对地的角速度 (2)欲使圆盘静止,人沿R/2圆周对圆盘的速度大小及方向 解:(1) 2V 0=00+ 21R (2)0=0→r=-21,R,方向与圆盘转动方向相同 2 例:大轮(M、R)可绕其轴 无摩擦转动,初角速0 小轮(m、r)可绕其轴 无摩擦转动,开始静止 求:两轮接触后最后的角速度 m 解:2R=0r 大轮:「-R=MR2-号MRa,=-R 小轮:jfd=)mr2a=fm 0 lMRQ-1MR0o=-ft 2mro=n 3
3 (2) 2 0 2 2 ( ) 2 1 ( ) 2 1 ( ) 2 1 m M V m M V k l l + A = + B + − m M k l l m M mV VB + − − + = 2 0 2 0 ( ) ( ) (M + m)VA l 0 = (M + m)VB lsin 2 0 2 0 2 0 0 0 ( ) ( ) sin l m V m M k l l mV l V l V l B A − + − = = 例:圆盘( m、 R )可绕通过其中 心的竖直光滑轴转动,有一人 V 静止( m = m/10 )站在 R/ 2 处 m m 开始圆盘载人以匀角速 0 转动 O R/ 2 如果此人沿垂直半径方向相对 R 0 圆盘以速率 V 作圆周运动,运 动方向与圆盘转动方向相反 求:(1)圆盘对地的角速度 (2)欲使圆盘静止,人沿 R/ 2 圆周对圆盘的速度大小及方向 解:(1) = + − + + / 2 ) 2 ( 2 1 ) 2 ( 2 1 2 2 0 2 2 R R V mR m R mR m R V 21 2 = 0 + (2) 2 21 0 0R V = = − ,方向与圆盘转动方向相同 例:大轮( M 、 R )可绕其轴 0 无摩擦转动,初角速 0 M R 小轮( m、 r )可绕其轴 O f 无摩擦转动,开始静止 求:两轮接触后最后的角速度 m O f r 解: R =r 大轮: − = − = − t fRdt MR MR fRt 0 0 2 2 2 1 2 1 小轮: frdt mr frt t = = 0 2 2 1 MR − MR = − ft 0 2 1 2 1 mr = ft 2 1

MRO-MR@+mro=0 2= Moo R Moo :多0= m+M rm+M
4 MR − MR0 + mr = 0 m M M + = 0 , m M M r R + = 0