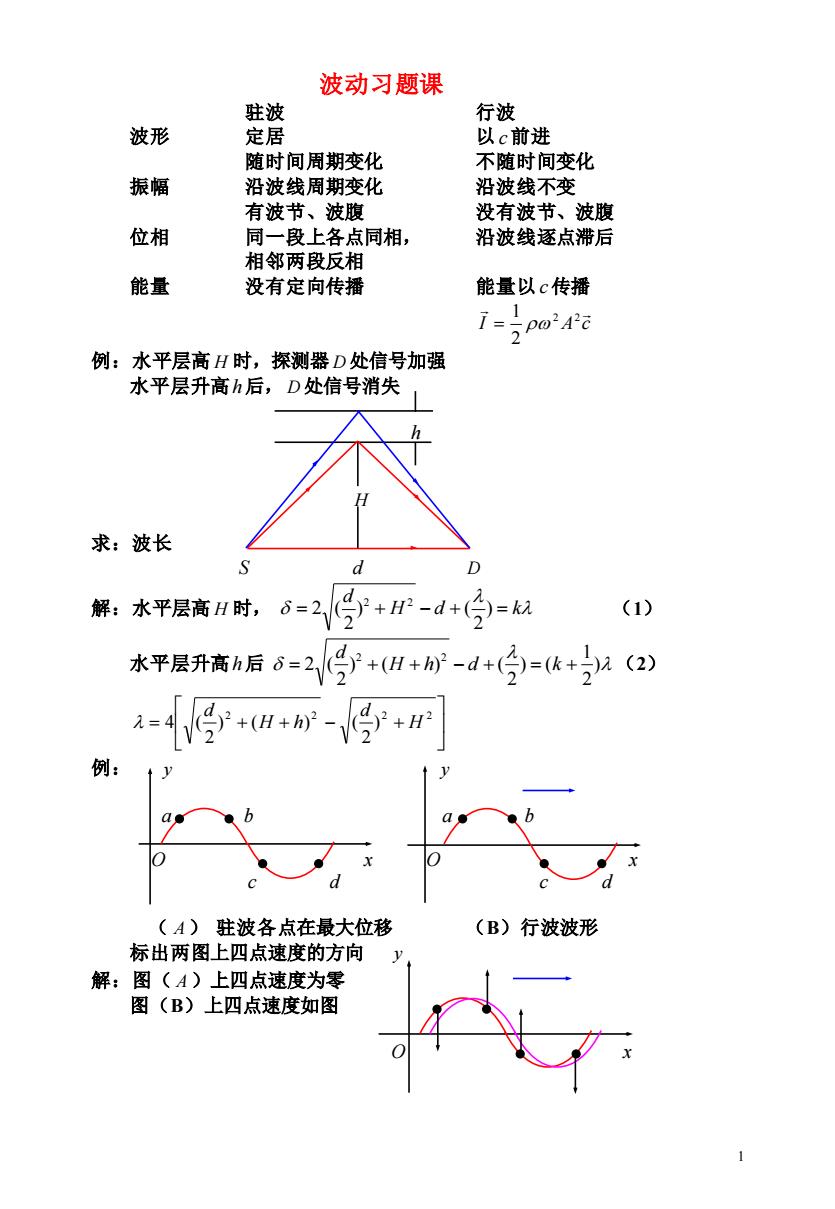
波动习题课 驻波 行波 波形 定居 以c前进 随时间周期变化 不随时间变化 振幅 沿波线周期变化 沿波线不变 有波节、波腹 没有波节、波腹 位相 同一段上各点同相, 沿波线逐点滞后 相邻两段反相 能量 没有定向传播 能量以c传播 1p0 例:水平层高H时,探测器D处信号加强 水平层升高h后,D处信号消失 求:波长 d D 解:水平层高H时,6=2号2+H-d+(宁=从 (1) 水平层升高h后6=2月+(H+-d+(=(k+n(2) 2=学+(1+-停+ 例: (A)驻波各点在最大位移 (B)行波波形 标出两图上四点速度的方向 解:图(A)上四点速度为零 图(B)上四点速度如图
1 波动习题课 驻波 行波 波形 定居 以 c 前进 随时间周期变化 不随时间变化 振幅 沿波线周期变化 沿波线不变 有波节、波腹 没有波节、波腹 位相 同一段上各点同相, 沿波线逐点滞后 相邻两段反相 能量 没有定向传播 能量以 c 传播 I A c 2 2 2 1 = 例:水平层高 H 时,探测器 D 处信号加强 水平层升高 h 后, D 处信号消失 h H 求:波长 S d D 解:水平层高 H 时, H d k d = + − + ) = 2 ) ( 2 2 ( 2 2 (1) 水平层升高 h 后 ) 2 1 ) ( 2 ) ( ) ( 2 2 ( 2 2 = + H + h − d + = k + d (2) = + + − + 2 2 2 2 ) 2 ) ( ) ( 2 4 ( H d H h d 例: y y a b a b O x O x c d c d ( A ) 驻波各点在最大位移 (B)行波波形 标出两图上四点速度的方向 y 解:图( A )上四点速度为零 图(B)上四点速度如图 O x

例:图为一向右传播的简谐波1时刻的波形曲线,BC是波密媒质 反射面,反射波1时刻的波形曲线为 解: (A) 例:沿x轴正向传播的平面谐波,频 率v,振幅A、已知1=1。时的波形 求:yo() 解:设yo()=Acos(2πt+p) 1=t。,O点位相 2π40+p= π -2πMo 2 Yo(=Acos(2rw+-2)=Acos[2rM-)+] 例:沿x轴正向传播的 平面谐波,x、x2 两点振动曲线如图 尸 己知,x2>x1,x2-xx1,中2<①1,0<Φ1-Φ2=1-p2<2π 2 2’0=0,9,只能取 or-I. 2’0-9,=-3z 2 4p-、2π 交。、_公9λ==九,A=2=心、3 7 2π4 cc 4
2 例:图为一向右传播的简谐波 t 时刻的波形曲线,BC 是波密媒质 反射面,反射波 t 时刻的波形曲线为[ ] y c B x P C P P (A) (B) P P (C) (D) 解: B P C P P (A) (B) 例:沿 x 轴正向传播的平面谐波,频 y c 0 t = t 率 ,振幅 A 、已知 0 t = t 时的波形 求: y (t) O O x 解:设 y (t) O = Acos(2t +) y c 0 t = t , O 点位相 2 2 0 t + = , 2 0 2 t = − O x y (t) O = 2 ) 2 cos(2 0 A t t + − = ] 2 cos[2 ( ) 0 A t − t + 例:沿 x 轴正向传播的 1 y 2 y 平面谐波, 1 x 、 2 x 两点振动曲线如图 T / 2 t T / 4 t 已知, 2 x 1 x , x2 − x1 求:波由 1 x → 2 x ,t =? T 解: 2 x 1 x , 2 1,0 1 −2 =1 −2 2 2 2 3 1 = or − , 2 = 0,1 只能取 2 3 , 2 3 2 1 − = − 2 = − , 4 3 2 = = − , t = c T c c x x 4 3 / 4 2 1 3 = = = −

例:一简谐波沿x轴正向传播, 已知x=0处质点振动曲线 试画出t=T时的波形曲线 解:b=dcoor--经 X=0 (.)=Acosto( t=T, A t=7 )=4coso7-总-1 =Acos(x+Z)=-Asin 2n 例:图为一简谐波t=2s时的波形曲线 A=0.2m,T=4s I= 2 求:yp() 解:设yp0)=0.2cos(1+p)m) 1=2,gx2+0= 2 9=-号 y0-02co经1-3m 例:图为一简谐波t=2s时的波形曲线1y(m) 求:yp(t) 0.01 t=2s c=200m/s 解:1=200m,c=200m/s 0.005 --●P v==1 -100m 设yp()=0.01cos(2t+p) t=2s,0.005=0.01cos(4π+p) Ap t=2s cos(4π+p)=1/2 4n+p- 3 y,0=0.01cos(2m+于-4m)=0.01cos(2a+3Xm 3
3 例:一简谐波沿 x 轴正向传播, y 已知 x = 0 处质点振动曲线 试画出 t = T 时的波形曲线 T t 解: ) 2 cos( yO = A t − x = 0 ] 2 ( , ) cos[ ( ) = − − c x y x t A t y t = T , A c t = T ] 2 cos[ ] 2 ( , ) cos[ ( ) = − − = − − c x A T c x y x T A T O x = x A c x A 2 ) sin 2 cos( + = − 例:图为一简谐波 t = 2s 时的波形曲线 y A = 0.2m, T = 4s u t = 2s 求: y (t) P 解:设 y (t) P = ) 2 0.2cos( t + (m) O P x t = 2s, 2 + 2 = 2 y 2 = − O P x y (t) P = ) 2 2 0.2cos( t − (m) 例:图为一简谐波 t = 2s 时的波形曲线 y (m) 求: y (t) P 0.01 t = 2s c = 200m/s 解: = 200m, c = 200m/s 0.005 P Hz c = = 1 O x 设 y (t) P = 0.01cos(2t +) t = 2s, 0.005 = 0.01cos(4 +) AP t = 2s cos(4 +) = 1/ 2 3 4 + = O y 4 3 = − y (t) P = )( ) 3 4 ) 0.01cos(2 3 0.01cos(2 t t m + − = + A 100m

例:图为一简谐波t=2s时的 ty (m)t=2s 波形曲线 0.5 -c=0.5m/s 求:yo() /2x(m) 解:A=0.5m,元=2m,c=0.5m/sy "=025 设yo0=05c0(受1+p) t=2s,7×2+0=-7 2 2 、 %0-05cow91-=05ca1+回 3π 22 例:一平面谐波沿x轴正向传播,A=10cm,o=7π(rad/s) t=ls,x。=10cm,y。=0, 必).0 2>10cm 求:y(x,) 解:设x,)=0.1cos7π1-+p] 0一 A t=1s t=1s Φ。=7x1-0马+p= (1) 2 0.2 Φ。=7π(1-02)+p=-T (2) 3 不能取贸 (Φ6<中。,0<Φ。-Φ。<2π) ①-(2:7z01_5江,c=0.84m/s 代入(10:0=子-7-0)=-17=-6x+ 2 0.84 3 x0=01eos7-04+学m 4
4 例:图为一简谐波 t = 2s 时的 y (m) t = 2s 波形曲线 0.5 c = 0.5m/s 求: y (t) O O 1 2 x (m) 解: A = 0.5m, = 2m,c = 0.5m/s y Hz c = = 0.25 设 y (t) O = ) 2 0.5cos( t + O x t = 2s, 2 2 2 + = − 2 3 = − , y (t) O = ) 2 2 ) 0.5cos( 2 3 2 0.5cos( t − = t + (m) 例:一平面谐波沿 x 轴正向传播, A =10cm, = 7 (rad /s) t =1s, xa = 10cm, ya = 0, ( ) 0 a t y xb = 20cm, yb = 5cm, ( ) 0 b t y 10cm 求: y(x,t) 解:设 y(x,t)= 0.1cos[7 ( − ) +] c x t Aa t =1s t =1s 2 ) 0.1 7 (1 = − + = c a (1) O y 3 ) 0.2 7 (1 = − + = − c b (2) Ab 不能取 3 5 ( b a , 0 a − b 2 ) (1) − (2) : 6 0.1 5 7 = c , c = 0.84m/s 代入(1): 3 6 3 17 ) 0.84 0.1 7 (1 2 = − − = − = − + y(x,t)= ]( ) 3 ) 0.84 0.1cos[7 ( m x t − +