
第三章单电子原子 3.1用薛定谔方程求解氢原子 3.2跃迁的选择定则 3.3电子自旋 3.4自旋和轨道相互作用 3.5单电子原子的精细结构
第三章 单电子原子 3.1 用薛定谔方程求解氢原子 3.2 跃迁的选择定则 3.3 电子自旋 3.4 自旋和轨道相互作用 3.5 单电子原子的精细结构

§3.1用薛定谔方程求解氢原子 库仑势 V)=- Ze2 i=- V2、 Ze2 4π1 2m 4π8o' V2Ψ- Ψ=EΨ V2Ψ 2m 4π8r 2 Ψ=0 2m(E+46 球坐标系v2= 1a o2 分离变量 Ψ(r,0,p)=R(r)Y(0,p) Q R O'Y 2mr2 dr sin 000 EI RY-0 方2 1 2mr2 1∂2Y R dr 29
§3.1 用薛定谔方程求解氢原子 • 库仑势 2 0 ( ) 4 Ze V r r 2 2 2 0 ˆ 2 4 Ze H m r 2 2 2 2 2 2 2 2 1 1 1 ( ) (sin ) sin sin r r r r r r ( , , ) ( ) ( , ) r R r Y 2 2 2 0 2 ( ) 0 4 m Ze E r 2 2 2 0 2 4 Ze E m r 2 2 2 2 2 2 2 0 d d 2 ( ) (sin ) [ ] 0 d d sin sin 4 R R Y R Y mr Ze r Y E RY r r r 2 2 2 2 2 2 2 0 1 d d 2 1 1 1 ( ) [ ] [ (sin ) ] d d 4 sin sin R mr Ze Y Y r E R r r r Y 分离变量 球坐标系

Z x
x y z r
R dr R dr Y(0,p)=⊙(0)Φ(p) (sinod-11d'Φ de Φsin0do2 sinθd (sin +sin20=- 1d2Φ ⊙d0 do 本d0 sine d 1d2Φ ⊙d m0912sm0r Φdo2
2 2 2 2 0 1 d d 2 ( ) [ ] d d 4 R mr Ze r E R r r r 2 2 2 1 1 1 [ (sin ) ] sin sin Y Y Y 2 2 2 2 0 1 d d 2 ( ) ( ) 0 d d 4 R mr Ze r E R r r r Y( , ) ( ) ( ) 2 2 2 1 1 d d 1 1 d (sin ) sin d d sin d 2 2 2 sin d d 1 d (sin ) sin d d d sin d d 2 (sin ) sin d d 2 2 1 d d

1d2Φ d2Φ +Φ=0 Φdo2 do2 Φ(p)=Aeo Φ(p+2π)=Φ(p) eivw(o+2m)=etitvp etivv2r =1 vv=m ④(p)=Aemo m=0,±1,+2,… AedoAdo=274=1 A=N2元 枣
2 2 d 0 d ( ) e i A ( 2 ) ( ) ( 2 ) e e i i 2 1 i e m ( ) im Ae 2 2 2 2 2 0 0 | | d d 2 1 im Ae A A 1 2 A 1 ( ) e 2 im m 2 2 1 d d m 0, 1, 2

sine d (sin +isin20=v v=m do 1 d sine do m09+-9-0 只有当2=1+) 为整数 且1≥ml 上述方程有解⊙n(O=BP(cos0)享 其中l-炉g-维台Legndre的数 du Yn(8,p)=⊙nm(O)Φm(p)=NmP(cos0)em 对于每一个l,m=-1,-1+1,…,-1,0,1,…1-1,1 Nm=V(1-|m)(2I+1)/4π(I+|mD月 归一化因子
2 2 1 d d (sin ) ( ) 0 sin d d sin m l l( 1) 且l m | | ( ) (cos ) m lm l BP l为整数 对于每一个l m l l l l , , 1, , 1,0,1, 1, | | | | 2 2 2 | | 2 1 d ( ) (1 ) ( 1) 2 ! d m l m m l l m l P u u u l u 缔合Legendre函数 ( , ) ( ) ( ) Ylm lm m ( | |)!(2 1) / 4 ( | |)! N l m l l m lm 归一化因子 sin d d 2 (sin ) sin d d m 只有当 上述方程有解 其中 (cos ) m im N P e lm l

Ynm(0,p)=⊙nm(O)Φm(p) 球谐函数 的号m0易动忘-0:
2 2 2 1 1 1 [ (sin ) ] sin sin lm lm lm Y Y Y 2 2 2 2 2 1 1 [ (sin ) ] ( 1) sin sin Y l l Y lm lm ( , ) ( ) ( ) Ylm lm m 球谐函数 l l( 1)

20》-0 、 R dr 方 r竖”=0 参量代换 R)=20p=2Z2m,n=2m Ze n= 2hVE4πE 该方程总有解,能量E可以取任意正值,非量子化 F<有2+片-0=0
2 2 2 2 0 1 d d 2 ( ) ( ) ( 1) 0 d d 4 R mr Ze r E l l R r r r 2 2 2 2 2 0 1 d d 2 ( 1) ( ) [ ( ) ] 0 d d 4 R m Ze l l r E R r r r r r ( ) ( ) r R r r 2 2 | | Z m E r 2 0 2 2 | | 4 m Ze n E 2 2 2 d ( ) 1 ( 1) 0, { } ( ) 0 d 4 n l l E 有 2 2 2 d ( ) 1 ( 1) 0, { } ( ) 0 d 4 n l l E 有 参量代换 该方程总有解,能量E可以取任意正值,非量子化

2+片&x0=0 do? 只有n=1,2,3.·且对于每一个n,1=0,1,2…n-1 ◆有解R(p)=Cmp'e2L(p)缔合Laguerre多项式 2Zme2 2Zr P=P,= C=2+ n4πh na na,2n[(n+)] n--】 L'(p)=∑(-1) [(n+I)]2p k=0 (n-1-1-k)(21+1+k)!k! +平wm(r,B,p)=R(r)en(O)Φn(p) n,l,m是量子数,为本征态的标志
2 2 1 ( ) e ( ) l l R C L nl nl n l 缔合Laguerre多项式 1 2 2 1 1 0 [( )!] ( ) ( 1) ( 1 )!(2 1 )! ! n l k l k n l k n l L n l k l k k 只有n 1,2,3 且对于每一个n l n , 0,1,2 1 ( , , ) ( ) ( ) ( ) nlm nl lm m r R r n,l,m是量子数,为本征态的标志 1 3 2 3 1 2 [ ( 1)]! {( ) } 2 [( )!] nl Z n l C na n n l 2 2 2 d ( ) 1 ( 1) { } ( ) 0 d 4 n l l 有解 2 0 1 2 2 4 n Zme Zr r n na
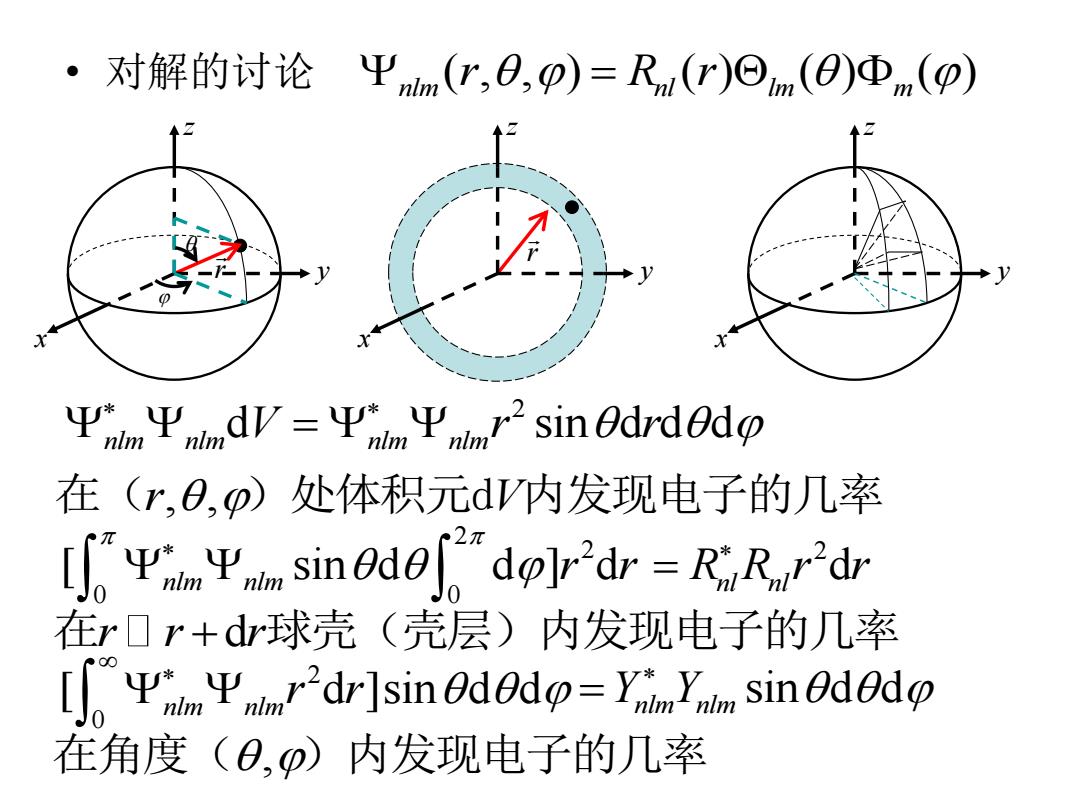
·对解的讨论 Ψnm(r,O,p)=Rnu(r)Om(O)Φm(p) 平m,平,mdV=ΨwnΨwmr2sin0 drdOdp 在(r,O,0)处体积元dV内发现电子的几率 2π [ΨmΨsined0dp]r2dr=PRr2dr 在r口"+d球壳(壳层)内发现电子的几率 [n平nm平namr2dr]小sin@dOdp=Ynim Y,sineded 在角度(θ,0)内发现电子的几率
• 对解的讨论 ( , , ) ( ) ( ) ( ) nlm nl lm m r R r x y z r 2 d sin d d d nlm nlm nlm nlm V r r 在(r V , , )处体积元d 内发现电子的几率 2 2 0 0 [ sin d d ] d nlm nlm r r 在r r r d 球壳(壳层)内发现电子的几率 x y z r 2 d R R r r nl nl 2 0 [ d ]sin d d nlm nlmr r sin d d Y Y nlm nlm 在角度( , )内发现电子的几率 x y z