
质点和质点系动力学 第1节牛顿运动定律 惯性→惯性定律 第一定律一 力三加速度 第二定律: F=kma F=ma 质点动力学方程 说明:1、F是合外力 m大→a小→惯性大 2、F相同时 m小三a大→惯性小 质量是物体惯性大小的量度 3、直角坐标系 v dv F.ma,=m- ,F,=ma,=m F.=ma.=m- v. dt dt dt 自然坐标系 F,ma,=m- F ma =m- t 第三定律:匠=-万 F 作用力与反作用力总是大小相等 方向相反且在同一条直线上 注意:作用力与反作用力同时出现、 同时消失,分别作用在两个物体上,两个力的种类相同 第2节国际单位制和量纲 一、国际单位制(SI) 长度,质量, 时间, 电流强度, 热力学温度 米(m), 千克(kg), 秒(s), 安培(A),开(K) 物质的量, 发光强度 基本量三导出量 摩尔(mol), 坎(cd) 基本单位一导出单位 例:速度,下= ms; _dt 加速度,a=d严 dh’ns2 力,F=md,kgms2=N(牛顿) 二、量纲:基本量的组合式 L(长度),M(质量),T(时间), V]=LT- [a=LT-2,[o=T,[F]=MLT-2, LT-L=LT- 0 注意:只有量纲相同的项才能相加减或划等号 x=1+2a -t,VA-irT-t,of-F- 1
1 质点和质点系动力学 第 1 节 牛顿运动定律 第一定律 力 加速度 惯性 惯性定律 第二定律: F kma = F ma = 质点动力学方程 说明:1、 F 是合外力 2、 F 相同时 小 大 惯性小 大 小 惯性大 m a m a 质量是物体惯性大小的量度 3、直角坐标系 dt dV F ma m x x = x = , dt dV F ma m y y = y = , dt dV F ma m z z = z = 自然坐标系 dt dV Ft = mat = m , 2 V Fn = man = m 第三定律: F1 F2 = − F2 F1 作用力与反作用力总是大小相等 A B 方向相反且在同一条直线上 注意:作用力与反作用力同时出现、 同时消失,分别作用在两个物体上,两个力的种类相同 第 2 节 国际单位制和量纲 一、国际单位制(SI) 长度, 质量, 时间, 电流强度, 热力学温度 米(m), 千克(kg), 秒(s), 安培(A), 开(K) 物质的量, 发光强度 基本量 导出量 摩尔(mol), 坎(cd) 基本单位 导出单位 例:速度, dt dr V = , −1 ms ; 加速度, dt dV a = , −2 ms 力, F ma = , kgms = N −2 (牛顿) 二、量纲:基本量的组合式 L (长度), M (质量), T (时间), −1 V = LT −2 a = LT , 1 [ ] − = T , −2 F = MLT , 2 2 1 2 2 − − − = = L T L LT V 注意:只有量纲相同的项才能相加减或划等号 2 2 0 2 1 x = V t + a t x = L, V t = LT T = L −1 0 , 2 2 2 2 2 2 2 ( ) 2 1 − − = = a t LT T L T
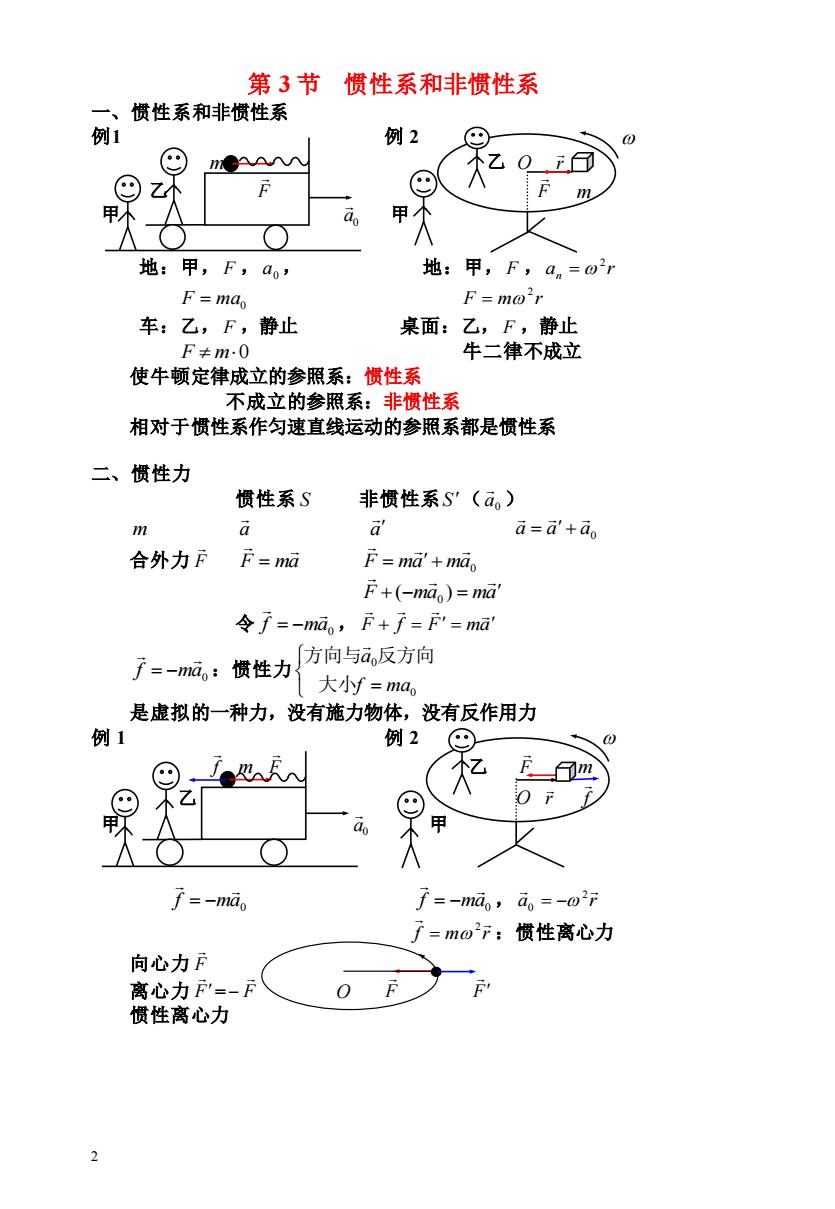
第3节 惯性系和非惯性系 、 惯性系和非惯性系 例1 例2 m 甲个 地:甲,F,a, 地:甲,F,an=o21 F=mdo F=mo'r 车:乙,F,静止 桌面:乙,F,静止 F≠m.0 牛二律不成立 使牛顿定律成立的参照系:惯性系 不成立的参照系:非惯性系 相对于惯性系作匀速直线运动的参照系都是惯性系 二、惯性力 惯性系S 非惯性系S'(a) m a a a=a'+ao 合外力F F=ma F=ma'+mdo F+(-mdo)=ma' 令子=-ma。,F+子-F'=ma 子=-ma。:惯性力 方向与a反方向 大小f=ma 是虚拟的一种力,没有施力物体,没有反作用力 例1 例2 f=-mdo f=-ma,a。=-027 子=mo2行:惯性离心力 向心力F 离心力F=-F F 惯性离心力 2
2 第 3 节 惯性系和非惯性系 一、惯性系和非惯性系 例1 例 2 m 乙 O r 乙 F F m 甲 0 a 甲 地:甲, F , 0 a , 地:甲, F ,a r n 2 = F = ma0 F m r 2 = 车:乙, F ,静止 桌面:乙, F ,静止 F m0 牛二律不成立 使牛顿定律成立的参照系:惯性系 不成立的参照系:非惯性系 相对于惯性系作匀速直线运动的参照系都是惯性系 二、惯性力 惯性系 S 非惯性系 S ( 0 a ) m a a a a a0 = + 合外力 F F ma = F ma ma0 = + F + −ma = ma ( ) 0 令 ma0 f = − , F + f = F = ma ma0 f = − :惯性力 = 0 0 f ma a 大小 方向与 反方向 是虚拟的一种力,没有施力物体,没有反作用力 例 1 例 2 f m F 乙 F m 乙 O r f 甲 0 a 甲 ma0 f = − ma0 f = − , a r 2 0 = − f m r 2 = :惯性离心力 向心力 F 离心力 F = F − O F F 惯性离心力

例:绳长1,一端固定,另一端 0 系一质量m的小球,在水平 10 位置将小球无初速释放, T 求:小球转过0角时的速率及绳中张力。 解:E=mg cos0=m业 (1), dt V2 Fn=T-mgsi血6=m7 (2), mg dv dy de ds dvv =gcose, dt do ds dt =gcos0, deT=gcos0 vav-glcosato,-glsin e,v-2glsn .P2 (2):T=mgsin 0+m=3mgsin 0 1 例:质量为M的质点沿x轴正向运动 M v=kx 求:F,x→x,△t? Xo x 解:F=a=M- MkV Mk'x dt dt v==ka,=kd,「 _dt In=,A=IIn Xo k xo 例:质量为m的质点仅在力F=k二作用 m 下运动,质点在r=处无初速释放,0干,F 求:质点到达无穷远处的速度 -ma= 解:F= nd业,d业_k1,dWd-k1 d’dm’m -,--北点,- mrm 例:定滑轮,物体M,人m=M/2相对绳子以加速度a。向上爬, 人对地面的加速度(向上为正): A,(2a+g)/3 B,-(3g-a) C,-(2a+g)/3 4 Mg D,ao m M M g-T=Ma绳地’m=M/2 T-mg=ma人地,a人地=a0+a绳地 mg Mg Mg 3
3 例:绳长 l ,一端固定,另一端 O l 系一质量 m 的小球,在水平 位置将小球无初速释放, T 求:小球转过 角时的速率及绳中张力。 m 解: dt dV Ft = mg cos = m (1), l V Fn T mg m 2 = − sin = (2), mg (1): g cos dt dV = , g cos dt ds ds d d dV = , g cos l V d dV = = 0 0 VdV gl cos d V , sin 2 1 2 V = gl ,V = 2glsin (2): sin 3 sin 2 mg l V T = mg + m = 例:质量为 M 的质点沿 x 轴正向运动 M V = kx 求: F , 0 1 x → x ,t ? 0 x x 1 x x 解: MkV Mk x dt dx Mk dt dV F Ma M 2 = = = = = kx dt dx V = = , kdt x dx = , = 1 0 1 0 t t x x kdt x dx k t x x = 0 1 ln , 0 1 ln 1 x x k t = 例:质量为 m 的质点仅在力 3 r r F k = 作用 m 下运动,质点在 0 r = r 处无初速释放,O 0 r r , F 求:质点到达无穷远处的速度 解: dt dV ma m r k F = = = 2 , 2 1 m r k dt dV = , 2 1 m r k dt dr dr dV = dr m r k VdV r V 2 0 1 0 = , 0 0 2 ) 1 ( 2 1 mr k m r r k V = = − , 2 /( ) mr0 V = k 例:定滑轮,物体 M ,人 m = M / 2 相对绳子以加速度 0 a 向上爬, 人对地面的加速度(向上为正): A, (2a0 + g)/ 3 B, (3 ) 0 − g − a C, − (2a0 + g)/ 3 0 a D, 0 a M Mg −T = Ma绳地 , m = M / 2 T − mg = ma人地 , a人地 = a0 + a绳地 m MgT Mg MgT Mg mg Mg
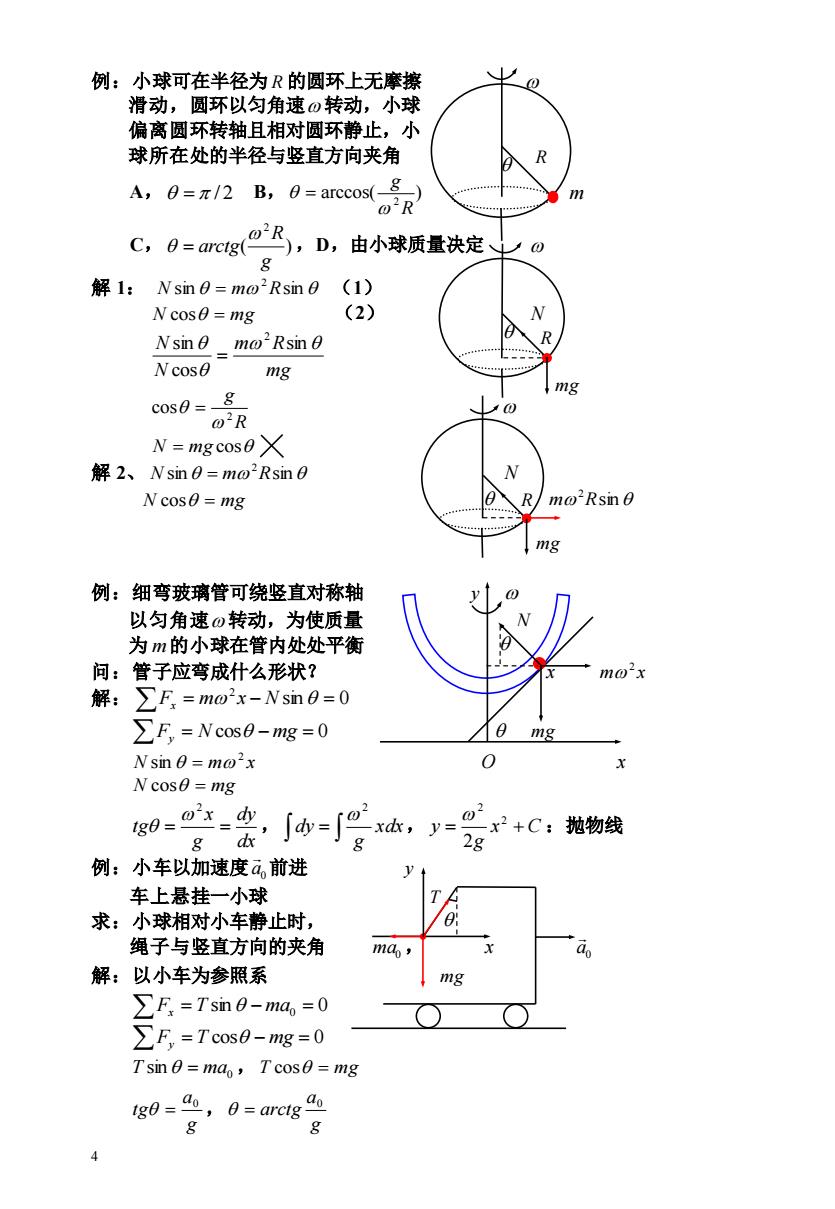
例:小球可在半径为R的圆环上无摩擦 滑动,圆环以匀角速0转动,小球 偏离圆环转轴且相对圆环静止,小 球所在处的半径与竖直方向夹角 R A,0=7/2 B,0=arccos(g) m o'R C,0=am心gA,D,由小球质量决定0 解1:Nsim0=mo2Rsin0(1) N cos0=mg (2) Nsin 0 mo'Rsin 0 Wcosθ mg mg c0s0=8 o @2R N=mgcos0 解2、Nsin0=mo2Rsin0 N cos0=mg R mo'Rsin 0 mg 例:细弯玻璃管可绕竖直对称轴 以匀角速0转动,为使质量 为m的小球在管内处处平衡 问:管子应弯成什么形状? mo'x 解:∑F=mo2x-Nsn0=0 ∑F,=Vcos8-mg=0 mg Nsin 0=mox X N cos0=mg g0=0r、 8 C,dy=丁。x,y=e 一x2+C:抛物线 a 2g 例:小车以加速度ā,前进 车上悬挂一小球 求:小球相对小车静止时, 绳子与竖直方向的夹角 mds 解:以小车为参照系 mg ∑F=Tsn0-ma,=0 ∑F,=Tcos6-mg=0 Tsin 0 ma,Tcos0=mg 180=do,0=arctg do 4
4 例:小球可在半径为 R 的圆环上无摩擦 滑动,圆环以匀角速 转动,小球 偏离圆环转轴且相对圆环静止,小 球所在处的半径与竖直方向夹角 R A, = / 2 B, arccos( ) 2R g = m C, ( ) 2 g R arctg = ,D,由小球质量决定 解 1: sin sin 2 N = m R (1) N cos = mg (2) N mg m R N N sin cos sin 2 = R g 2 cos = N = mg cos 解 2、 sin sin 2 N = m R N N cos = mg R sin 2 m R mg 例:细弯玻璃管可绕竖直对称轴 y 以匀角速 转动,为使质量 N 为 m 的小球在管内处处平衡 问:管子应弯成什么形状? x m x 2 解: = − sin = 0 2 Fx m x N Fy = N cos − mg = 0 mg N m x 2 sin = O x N cos = mg dx dy g x tg = = 2 , = xdx g dy 2 , x C g y = + 2 2 2 :抛物线 例:小车以加速度 0 a 前进 y 车上悬挂一小球 T 求:小球相对小车静止时, 绳子与竖直方向的夹角 ma0 , x 0 a 解:以小车为参照系 mg Fx = T sin − ma0 = 0 Fy = T cos − mg = 0 0 T sin = ma ,T cos = mg g a tg 0 = , g a arctg 0 = mg R