
第四章氦原子和多电子原子 4.1氦原子的光谱和能级 4.2全同粒子和泡利不相容原理 4.3多电子原子的电子组态 4.4原子的壳层结构和元素周期表 4.5多电子原子的原子态和能级
第四章 氦原子和多电子原子 4.1 氦原子的光谱和能级 4.2 全同粒子和泡利不相容原理 4.3 多电子原子的电子组态 4.4 原子的壳层结构和元素周期表 4.5 多电子原子的原子态和能级

§4.1氦原子的光谱和能级 1、He原子的光谱和能级 ·核外有两个电子,有两套谱线,分别是三线和单 线的结构。能级有以下特点: 两套能级,一套单层,另一套三层,对应的原子多重态 称为单态和三重态,单态和三重态之间无跃迁 2 基态和第一激发态能量差很大,约为19.8ev 3 三重态能级低于相应的单态能级 4 n=1的原子态不存在三重态 5 第一激发态都是亚稳态,能级寿命长
§4.1 氦原子的光谱和能级 1、He原子的光谱和能级 • 核外有两个电子,有两套谱线,分别是三线和单 线的结构。能级有以下特点: ① 两套能级,一套单层,另一套三层,对应的原子多重态 称为单态和三重态,单态和三重态之间无跃迁 ② 基态和第一激发态能量差很大,约为19.8ev ③ 三重态能级低于相应的单态能级 ④ n=1的原子态不存在三重态 ⑤ 第一激发态都是亚稳态,能级寿命长
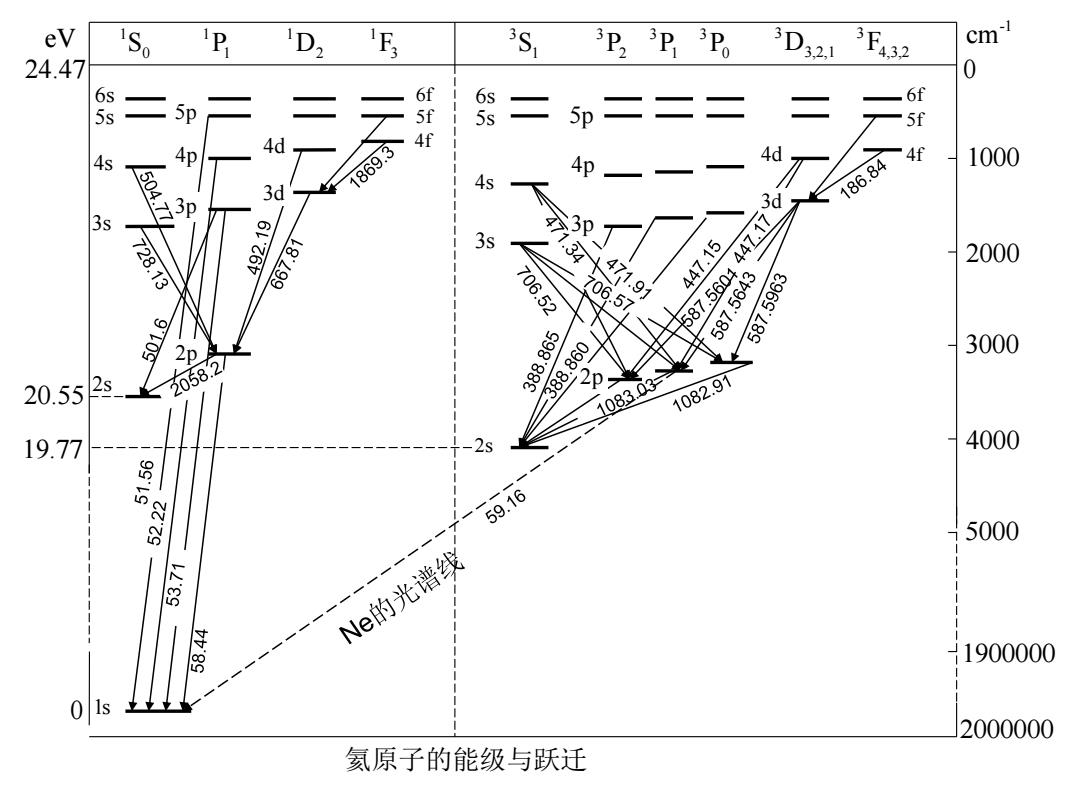
eV 1S。 P D,F 3Si 3D23D3P。 3D32 3F432 cm 24.47 0 二 6f 5p s 二 5p二二 55 4s 4d 4f 1869.3 4d 4p 4f 186.84 1000 3d 4s 3s 47 728.13 6-265 667.81 3s .3 706 471.91 44Z17 2000 706.57 447.15 587.560 587.564 587.5963 2p 3000 20.55 2s 2058.2 388.865 388.860 2p 1083.03 1082.91 19.77 2s 4000 80m 59.16 5000 Ne的光谱线 1900000 2000000 氦原子的能级与跃迁
1 S0 1 P1 1 D2 1 F3 1s2s 3s4s5s6s 2p4p5p 4d 3 S1 3 P0 3 D3,2,1 3 F4,3,2 3 P2 3 P1 -1 eV cm 24.47 0 20.55 19.770 2000000 5000 1900000 4000 3000 2000 1000 2s3s4s5s6s 2p 3p4p5p 4d 4f 5f 氦原子的能级与跃迁 3d 5f 3p 6f 6f 4f 3d

2、氦原子能级的简单讨论 在只有一个价电子的情况下,库仑作用仅 仅是价电子与原子核或原子实之间的作用 多个价电子的情况下,除了上述作用外, 还有价电子之间的相互作用(先忽略磁相 互作用) ·Hamilton量为 2m。 j
2、氦原子能级的简单讨论 • 在只有一个价电子的情况下,库仑作用仅 仅是价电子与原子核或原子实之间的作用 • 多个价电子的情况下,除了上述作用外, 还有价电子之间的相互作用(先忽略磁相 互作用) • Hamilton量为 2 2 2 1 1 e 0 0 1 ( ) 2 4 2 4 n n n i i i i j i ij p Z e e H m r r

。Hamilton方程 12心-含容高,= 其中-乃 所以,即使对于仅有两个价电子的情形,这个方程也无法 用分离变量法求解,或者无法得到解析解 可以尝试用“微扰论”求解上述方程,即将核与电子间的 相互作用看作是能量的主要部分,而将两个电子之间的相互作 用看作是小量,则主要能量的方程为 m>2=8 i=1 而微扰部分的方程为 4GwwC
• Hamilton方程 2 2 2 2 1 2 1 2 e 0 0 1 1 1 [ ] ( , , ) ( , , ) 2 4 2 4 N n N i N N i i i j i ij Z e e E m r r r r r r r r | | ij i j 其中r r r 所以,即使对于仅有两个价电子的情形,这个方程也无法 用分离变量法求解,或者无法得到解析解 可以尝试用“微扰论”求解上述方程,即将核与电子间的 相互作用看作是能量的主要部分,而将两个电子之间的相互作 用看作是小量,则主要能量的方程为 2 2 2 0 1 2 0 0 1 2 e 0 1 1 [ ] ( , , ) ( , , ) 2 4 n n i N N i i i Z e E m r r r r r r r • 而微扰部分的方程为 2 0 1 2 1 0 1 2 0 1 [ ] ( , , ) ( , , ) 2 4 N N N i j ij e E r r r r r r r

关于的方程可以用分离变量法求解,每一个解与氢原 子的解类似,氢的能量为 2π2m.e4Z2 1e2Z2 E (4πE)2h2n24π62a1n2 可得氦原子基态时总能量E为 2ex2=-54.4eVx2=-1088eV E0=一 4n8 2a 而微扰部分的本征函数可以用0代替,侧可求得两电子间 的相互作用能为 A(,)=△EWG, 5e2 ·考虑基态 △E,=三 =34.0eV o 电离能为 24πEi224π82a4 -54.4eV-(-108.8eV+34.0eV=-54.4eV-(-74.4eV=20.4eV ·实验值为24.58eV
• 关于E0的方程可以用分离变量法求解,每一个解与氢原 子的解类似,氢的能量为 2 4 2 2 2 e 2 2 2 2 0 0 1 2 1 (4 ) 4 2 n m e Z e Z E h n a n • 可得氦原子基态时总能量E0为 2 2 0 0 1 2 2 54.4eV 2 108.8eV 4 2 e E a • 而微扰部分的本征函数可以用ψ0代替,则可求得两电子间 的相互作用能为 2 0 1 2 1 0 1 2 0 12 1 [ ] ( , ) ( , ) 2 4 e E r r r r r • 考虑基态 2 2 1 0 12 0 1 1 5 34.0eV 2 4 2 4 2 e e E r a • 电离能为 54.4eV ( 108.8eV+34.0eV)= 54.4eV ( 74.4eV)=20.4eV • 实验值为24.58eV

§4.2全同粒子和Pauli不相容原理 1、全同粒子和波函数的交换对称性 ·内禀属性完全相同的粒子,称作全同粒子 所有电子都有相同的质量、电荷、大小以及自旋, 这是电子的内禀属性 ·电子是全同粒子,电子是不可分辨的,除非它们的 状态不同,或描述它们的量子数不同。 ·如果将两个电子相互交换,则原子的状态不发生任 何变化,这种特性被称作交换对称性
§4.2 全同粒子和Pauli不相容原理 1、全同粒子和波函数的交换对称性 • 内禀属性完全相同的粒子,称作全同粒子 • 所有电子都有相同的质量、电荷、大小以及自旋, 这是电子的内禀属性 • 电子是全同粒子,电子是不可分辨的,除非它们的 状态不同,或描述它们的量子数不同。 • 如果将两个电子相互交换,则原子的状态不发生任 何变化,这种特性被称作交换对称性

关于电子的交换对称性 o 两电子体系,包含自旋的坐标记为91、g2,波函数记为平 (q1,q2)。交换电子之后的波函数为Ψ(q2,q1)。 交换后,原子的状态不变,则有 |w(91,92)P=w(q2,91)2 如果波函数都用实函数表示 wW(91,92)=W(92,91) 交换对称性波函数 Ψ(91,92)=-w(92,91) 交换反对称性波函数
关于电子的交换对称性 • 两电子体系,包含自旋的坐标记为q1、q2,波函数记为Ψ ( q1,q2 )。交换电子之后的波函数为Ψ ( q2,q1 )。 交换后,原子的状态不变,则有 2 2 1 2 2 1 | ( , ) | | ( , ) | q q q q 如果波函数都用实函数表示 1 2 2 1 ( , ) ( , ) q q q q 1 2 2 1 ( , ) ( , ) q q q q 交换对称性波函数 交换反对称性波函数

如果两个电子是独立的,不考虑它们之间的相互作用,则可 以用分离变量法得出每一个电子的波函数Ψa(g1)、 ΨB(2),而系统的总波函数是二者的乘积 交换前后的波函数为Ψ=Ψa(q1)屮B(q2), ΨI=Ψa(g2)ΨB(g1) ·Ψ和ΨI不一定满足交换对称性 但下述线形组合一定满足对称性和反对称性 w,(4,4)-2[w.(4)w(ga)+w.(Ma(4】 w,(g.)=2w(4,wa(g)-.(gwn(g】
• 如果两个电子是独立的,不考虑它们之间的相互作用,则可 以用分离变量法得出每一个电子的波函数Ψ α (q1)、 Ψ β (q2) ,而系统的总波函数是二者的乘积 • 交换前后的波函数为Ψ I=Ψ α (q1)Ψ β (q2) , Ψ II=Ψ α (q2)Ψ β (q1) • Ψ I和Ψ II不一定满足交换对称性 • 但下述线形组合一定满足对称性和反对称性 1 2 1 2 2 1 1 ( , ) [ ( ) ( ) ( ) ( )] 2 S q q q q q q 1 2 1 2 2 1 1 ( , ) [ ( ) ( ) ( ) ( )] 2 A q q q q q q

2、泡利不相容原理 ·不能有两个电子处于同样的状态,也就是说原子中的任 意两个电子不能具有完全相同的四个量子数 ·如果全同粒子具有交换反对称性设两个粒子处于相同状 态a,其波函数为1 w.(,9)=2w.(g)w.(q2)-业.(9)w.(gi】 三0 具有交换反对称性的全同粒子,处于相同状态的几率为0 两个具有交换反对称性的全同粒子,不能处于相同状态 自旋量子数为半整数的粒子,具有交换反对称性;自旋量子数 为整数的粒子,具有交换对称性 电子(s=1/2)具有交换反对称性;光子(s=1)具有交换对称性 Pauli原理:多电子系统的波函数必定是交换反对称的
2、泡利不相容原理 • 不能有两个电子处于同样的状态,也就是说原子中的任 意两个电子不能具有完全相同的四个量子数 • 如果全同粒子具有交换反对称性设两个粒子处于相同状 态α,其波函数为 1 2 1 2 2 1 1 ( , ) [ ( ) ( ) ( ) ( )] 2 A q q q q q q 0 具有交换反对称性的全同粒子,处于相同状态的几率为0 两个具有交换反对称性的全同粒子,不能处于相同状态 自旋量子数为半整数的粒子,具有交换反对称性;自旋量子数 为整数的粒子,具有交换对称性 电子(s=1/2ħ)具有交换反对称性;光子(s=1ħ)具有交换对称性 Pauli原理:多电子系统的波函数必定是交换反对称的