
第一章波尔原子模型
第一章 波尔原子模型

§1.1卢瑟福模型 ·1、原子学说 ·2、原子的结构 ·3、卢瑟福模型
§1.1 卢瑟福模型 • 1、原子学说 • 2、原子的结构 • 3、卢瑟福模型

一、古代关于物质结构的观点 ·1、不可无限分割,存在最小的结构单元 “端,体之无序最前者也。”一《墨 子》。 ·序:次序、大小;最前:最初始的。 ·端是物质的最小结构单元。 “其小无内,谓之小一”一惠子。 atou0,希腊文“不可分割的”一德谟克 利特。 atom,旧译“莫破”,即原子
一、古代关于物质结构的观点 • 1、不可无限分割,存在最小的结构单元 • “端,体之无序最前者也。”——《墨 子》。 • 序:次序、大小;最前:最初始的。 • 端是物质的最小结构单元。 • “其小无内,谓之小一”——惠子。 • ατομα ,希腊文“不可分割的”——德谟克 利特。 • atom,旧译“莫破”,即原子

·2、可以无限分割,物质是连续的 “一尺之棰,日取其半,万世不竭。” 公孙龙 。 物质是连续的,可以无限地分割一亚里士 多德 ·这一观点从数学上看是正取的; ·从哲学上看似乎也是正确的; 但从物理上看,缺乏实验依据,所以没有物 理思想
• 2、可以无限分割,物质是连续的 • “一尺之棰,日取其半,万世不竭。”—— 公孙龙 • 物质是连续的,可以无限地分割——亚里士 多德 • 这一观点从数学上看是正取的; • 从哲学上看似乎也是正确的; • 但从物理上看,缺乏实验依据,所以没有物 理思想

二、近代原子观的建立 ·起始于对物质化学性质的研究 ·1806年,Proust(法):化合物的分子定组成定律。 ·1807年,John Dalton(1766-1844)(英):倍比定 律,最先提出原子论。 ·1808年,Gy-Lussac(法):化合体积定律。 1811年,Amede0 Avogadro(1776-1856)(意): Avogadro定律。 ·1826年,Brown(英):Brown运动。 ·1833年,Faraday(英):电解定律。 ·1869年,MeHeneeB(俄):元素周期律。 ·从化学上提出了单个原子的存在
二、近代原子观的建立 • 起始于对物质化学性质的研究 • 1806年,Proust(法):化合物的分子定组成定律。 • 1807年,John Dalton (1766–1844) (英):倍比定 律,最先提出原子论。 • 1808年,Gay-Lussac(法):化合体积定律。 • 1811年,Amedeo Avogadro (1776–1856)(意): Avogadro定律。 • 1826年,Brown(英):Brown运动。 • 1833年,Faraday(英):电解定律。 • 1869年,Менделеев(俄):元素周期律。 • 从化学上提出了单个原子的存在

三、原子的质量和体积 ·1、原子的质量 ·可以由原子量和由Avogadro:定律计算 ·Avogadro常数NA:1mol的原子的数量 ·原子量A:1mol的原子的质量 ·一个原子的质量 A M= NA W4=6.022×1023/mol
三、原子的质量和体积 • 1、原子的质量 • 可以由原子量和由Avogadro定律计算 • Avogadro常数NA: 1mol的原子的数量 • 原子量A:1mol的原子的质量 • 一个原子的质量 NA A M = 6.022 10 / mol 23 NA = ×
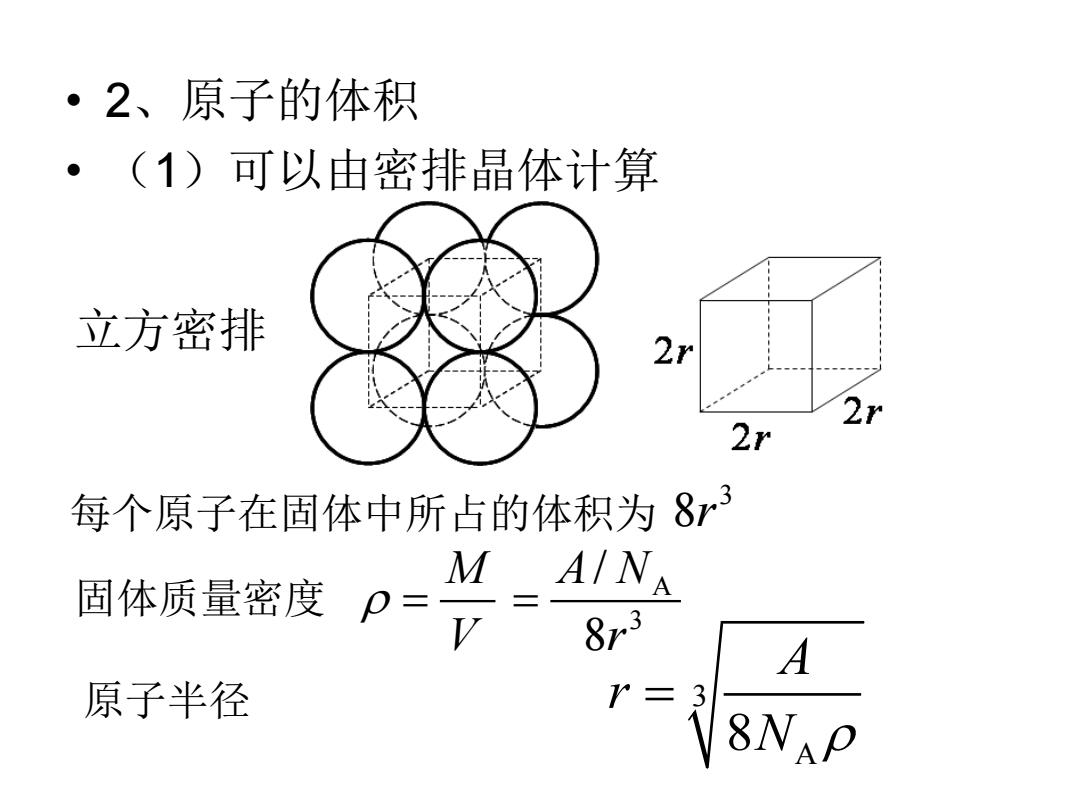
·2、原子的体积 (1)可以由密排晶体计算 立方密排 2r 2r 2r 每个原子在固体中所占的体积为83 M AINA 固体质量密度P= 8r3 A 原子半径 T-iSNAP
• 2、原子的体积 • (1)可以由密排晶体计算 M V ρ = 立方密排 3 每个原子在固体中所占的体积为 8r 3 A 8 A r N ρ = 固体质量密度 原子半径 A 3 / 8 A N r =

六角密排 3 2r 六棱柱的高 22-3-4 2¥ _r 底边长2r 每个原了所占的体积6××2r×V3r 46,16=42r 3 M AIN 质量密度 V 4V2r3 A 原子半径 4PN ~10-10m=1A
六棱柱的高 2 2 底边长 2 46 2 (2 ) ( 3 ) 3 3 rrr − = 2r 每个原子所占的体积 1 46 3 6 2 3 /6 4 2 2 3 ×× × × = rr r r 质量密度 A 3 / 4 2 M A N V r ρ = = ~ 3 4 2 A A r ρN 原子半径 六角密排 10 ~ 10 m 1A − =
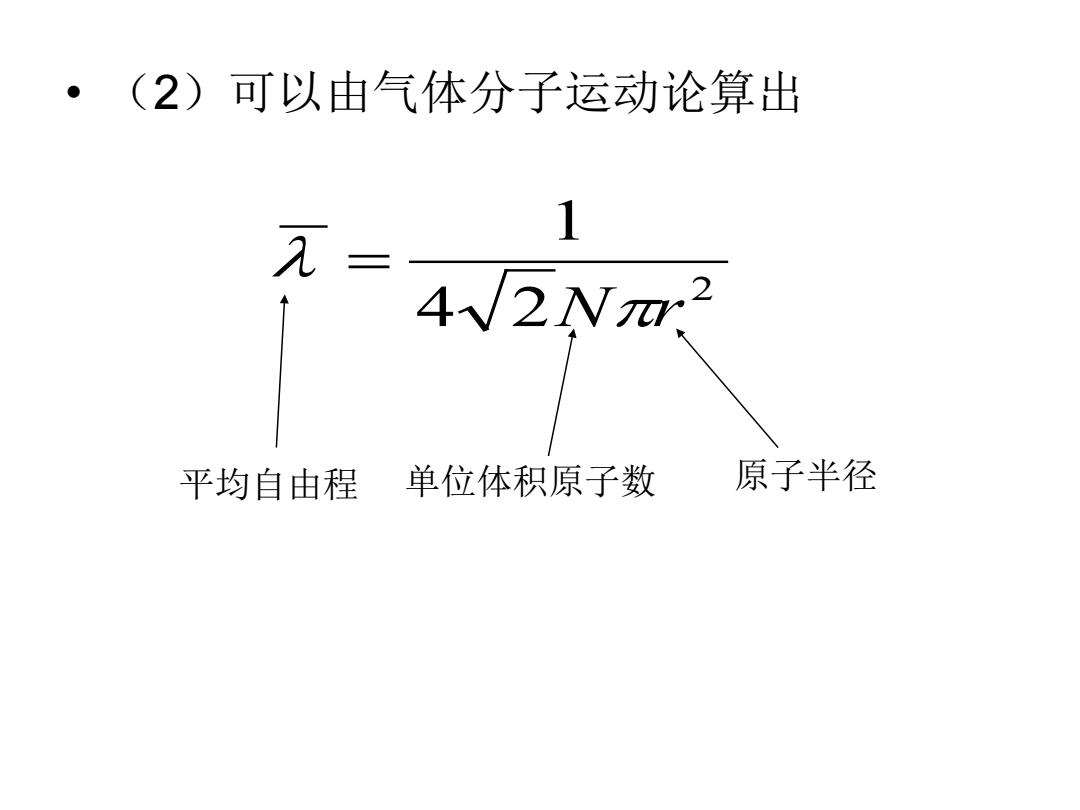
·(2)可以由气体分子运动论算出 1 4√2N2 平均自由程 单位体积原子数 原子半径
• (2)可以由气体分子运动论算出 2 4 2 1 Nπr λ = 平均自由程 单位体积原子数 原子半径

·(3)由von de Waals定律算出 (p+XV-b)=RT ·其中 b=4va Va 原子体积
• (3)由von de Waals定律算出 V b RT V a ( p + )( − ) = • 其中 b = 4Va Va 原子体积