
第3节简谐振动的合成 一、同方向同频率简谐振动的合成 x1=A cos(ot+p),x2=A cos(ot+p2) x=x+x2=4 cos(ot+)+4 cos(ot+) =A cosot cosp-A sin otsin p+A cosotcosp2-A sin otsin p2 =(A coso+42 cos2)cosot-(A sin o+sin )sin ot A coso+4 cos2=Acosp (1) A sin p+A2 sin p2 =Asin p (2) x=A cosotcoso-A sin otsin =A cos(ot+) 4=V4+45+244c0s0,-9),gp=4sn9+4s0 A coso+A cosz sin++-- cos+- p∈IⅡIIV 92-9=±2kπk=0,12,…, 同相,A=A+A最大 p2-9=(2k+1)πk=0,12,,反相,A=4-A最小 如果A=A2,A=0 0 旋转矢量法:A=A,+A, A=42+A2+24 42 cos(2-) A g0= A sm p+42 sm 2 A cos+42 cos2 x=X+x=Acos(ot+) 0 例:两个同方向同频率简谐振动,合振动A=20cm,合振动 与第一个简谐振动的位相差中-4=π/6,A=10W3cm 求:A及(4-4) A 解:A=A-A A2=A2+42-244 cos() A =10(cm), 0,P A2=A++2A,A2cos(中2-4) Cos(4-4)= ?--4=0,,-4=π/2 2A4 二、同方向不同频率简谐振动的合成 x=A cos(o t+) A x2=A2Cos(021+p2) XΦ 2t+p2t+p △Φ=Φ2-Φ1=(02-01)f+02-P1 1
1 第 3 节 简谐振动的合成 一、同方向同频率简谐振动的合成 cos( ) 1 = 1 +1 x A t , cos( ) 2 = 2 +2 x A t 1 2 x = x + x = cos( ) 1 +1 A t + cos( ) 2 +2 A t = 1 1 A cost cos 1 1 − A sintsin + 2 2 A cost cos 2 2 − A sintsin = (A cos A cos )cost 1 1 + 2 2 (A sin A sin )sint − 1 1 + 2 2 A1 cos1 + A2 cos2 = Acos (1) A1 sin1 + A2 sin2 = Asin (2) x = A cost cos − A sin tsin = A cos(t + ) 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − , 1 1 2 2 1 1 2 2 cos cos sin sin A A A A tg + + = sin + + - - cos + - - + V 2 −1 = 2k k = 0,1,2, , 同相, A = A1 + A2 最大 2 −1 = (2k +1) k = 0,1,2, ,反相, A = A1 − A2 最小 如果 A1 = A2 , A = 0 旋转矢量法: A A1 A2 = + A 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − A2 1 1 2 2 1 1 2 2 cos cos sin sin A A A A tg + + = 2 A1 cos( ) x = x1 + x2 = A t + O x 例:两个同方向同频率简谐振动,合振动 A =20cm,合振动 与第一个简谐振动的位相差 −1 = /6, A1 = 10 3cm 求: A2 及( 2 −1 ) A 解: A2 A A1 = − 2 cos( ) 1 1 2 1 2 A2 = A + A − AA − A2 A1 =10(cm), 2 1 2 cos( ) 1 2 2 1 2 2 2 1 2 A = A + A + A A − O x 0 2 cos( ) 1 2 2 2 2 1 2 2 1 = − − − = A A A A A ,2 −1 = / 2 二、同方向不同频率简谐振动的合成 A ,t cos( ) 1 = 1 1 +1 x A t A2 cos( ) 2 = 2 2 +2 x A t A1 2 +2 t 1 +1 t O x = 2 1 2 1 2 1 − = ( − )t + − A2 6 1

A=VA+A号+2A1A2cos[(o2-o)1+(p2-p1月 合振动不是简谐振动 A变化的周期x= 2π 02-01 4变化的频率v-上_-o=k,- 2元 A的变化表现为振动强弱的变化 振动忽强忽弱的现象称为“拍”,V=y2-y:拍频 2π T= 拍的周期 02-01 “拍”的示教 设02>01 02+ 1s内 A A2比A,多转角度o,-0 多转圈数,二=-y:拍频 2π 注意: 1、拍频是合振幅或振动强度变化的频率 不是合位移变化的频率 令A=A2 x=x+x2=A cos(@t+)+A cos(@2t+2) =24cos0,二01+%%)c00+01+%t%) 2 2 2 2 0+0>,@,A=24c0s0,0m1+% 2 2 2 2 拍周期π= π 2π 拍颜v=二m=k,-y 02-01 02-01 2π 2 2、山-较小时“拍”现象才比较明显 3、从x-t曲线上看“拍”现象,p257 4、A=A+A2只适用于同方向简谐振动的合成 三、相互垂直简谐振动的合成 ↑y 1、同频率: P(x,y) x=A cos(ot+) y=4 cos(ot+p2) 位移F=xi+ 轨迹方程: 茶 -cos(2-e)=sin(2- 2
2 2 cos[( ) ( )] 1 2 2 1 2 1 2 2 2 A = A1 + A + A A − t + − 合振动不是简谐振动 A 变化的周期 2 1 2 − = A 变化的频率 2 1 2 1 2 1 = − − = = A 的变化表现为振动强弱的变化 振动忽强忽弱的现象称为“拍”, = 2 − 1 :拍频 2 1 2 − = :拍的周期 “拍”的示教 设 2 1 2 A 1s 内 A2 1 A2 比 A1 多转角度 2 −1 A1 多转圈数 2 1 2 1 2 = − − :拍频 O x 注意: 1、拍频是合振幅或振动强度变化的频率 不是合位移变化的频率 令 A1 = A2 1 2 x = x + x = cos( ) 1 1 +1 A t + cos( ) 1 2 +2 A t = ) 2 2 )cos( 2 2 2 cos( 2 1 2 1 2 1 2 1 1 + + − + + − A t t 2 2 2 1 2 −1 + , ) 2 2 2 cos( 2 1 2 1 1 − + − A = A t 拍周期 2 1 2 1 2 2 − = − = ,拍频 2 1 2 1 2 1 = − − = = 2、 2 −1 较小时“拍”现象才比较明显 3、从 x −t 曲线上看“拍”现象,p257 4、 A A1 A2 = + 只适用于同方向简谐振动的合成 三、相互垂直简谐振动的合成 y 1、同频率: P (x, y) cos( ) = 1 +1 x A t cos( ) = 2 +2 y A t 位移 r xi yj = + O x 轨迹方程: cos( ) sin ( ) 2 2 1 2 2 1 1 2 2 2 2 2 1 2 + − − = − A A x y A y A x r
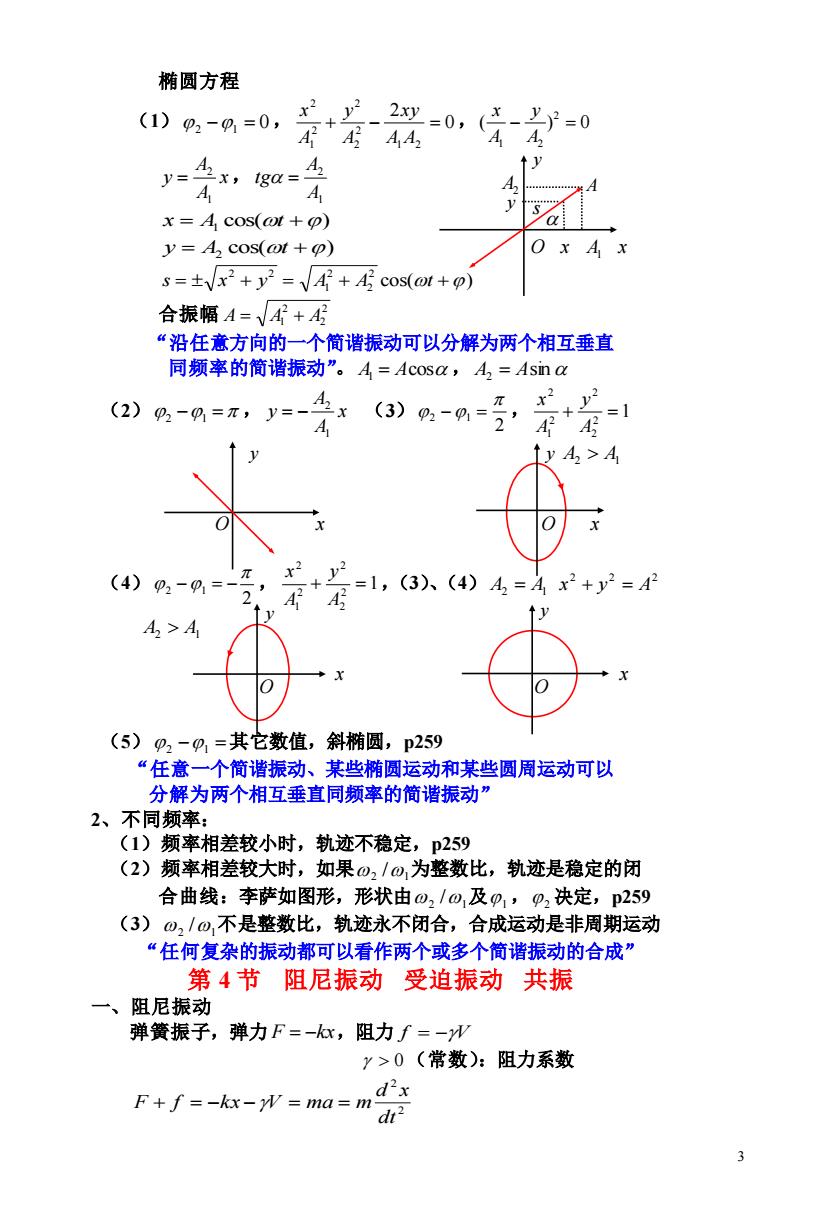
椭圆方程 (1)p2-0=0, x2,y2 2y=0,(-}=0 +44 AA x,iga= A A A x=A cos(ot + y=A cos(ot+) s=cos(or+o) 合振幅A=VA?+ “沿任意方向的一个简谐振动可以分解为两个相互垂直 同频率的简谐振动”。A=Acosa,A2=Asin a 2)-=x③99号,若 =1 A A y A>A (4)p2-9=- x 4R1,3)4)4=4+y=4 A>A (5)p2-1=其它数值,斜椭圆,p259 “任意一个简谐振动、某些椭圆运动和某些圆周运动可以 分解为两个相互垂直同频率的简谐振动” 2、不同频率: (1)频率相差较小时,轨迹不稳定,p259 (2)频率相差较大时,如果02/⊙,为整数比,轨迹是稳定的闭 合曲线:李萨如图形,形状由o2/0,及p,p2决定,p259 (3)⊙2/o⊙,不是整数比,轨迹永不闭合,合成运动是非周期运动 “任何复杂的振动都可以看作两个或多个简谐振动的合成” 第4节阻尼振动受迫振动共振 一、阻尼振动 弹簧振子,弹力F=-x,阻力f=一W y>0(常数):阻力系数 2x F+f=-kx-yV=ma=m- t2 3
3 椭圆方程 (1) 2 −1 = 0, 0 2 1 2 2 2 2 2 1 2 + − = A A xy A y A x ,( ) 0 2 1 2 − = A y A x x A A y 1 2 = , 1 2 A A tg = cos( ) x = A1 t + cos( ) y = A2 t + O x A1 x cos( ) 2 2 2 1 2 2 s = x + y = A + A t + 合振幅 2 2 2 A = A1 + A “沿任意方向的一个简谐振动可以分解为两个相互垂直 同频率的简谐振动”。 A1 = Acos , A2 = Asin (2) 2 −1 = , x A A y 1 2 = − (3) 2 2 1 − = , 1 2 2 2 2 1 2 + = A y A x y y A2 A1 x O x (4) 2 2 1 − = − , 1 2 2 2 2 1 2 + = A y A x ,(3)、(4) A2 = A1 2 2 2 x + y = A A2 A1 x x (5) 2 −1 = 其它数值,斜椭圆,p259 “任意一个简谐振动、某些椭圆运动和某些圆周运动可以 分解为两个相互垂直同频率的简谐振动” 2、不同频率: (1)频率相差较小时,轨迹不稳定,p259 (2)频率相差较大时,如果 2 1 / 为整数比,轨迹是稳定的闭 合曲线:李萨如图形,形状由 2 1 / 及 1, 2 决定,p259 (3) 2 1 / 不是整数比,轨迹永不闭合,合成运动是非周期运动 “任何复杂的振动都可以看作两个或多个简谐振动的合成” 第 4 节 阻尼振动 受迫振动 共振 一、阻尼振动 弹簧振子,弹力 F = −kx ,阻力 f = −V 0 (常数):阻力系数 2 2 dt d x F + f = −kx −V = ma = m O y y s y A2 y A O O

dixk +-x=0 di2 mdt m 令Vk/m=o:固有频率,y/m=2B,B>0:阻尼因子 d2x +2乃+x=0一一阻厄辰动藏分方程 d 1、小阻尼(欠阻尼)B0o x=Ce←B+VB2-a5n +Ce(-B-1B-oin 临界阻尼B=o。,x=(C1+c2t)eA 二、受迫振动 周期性外力:强迫力,受迫振动 弹簧振子,弹力F=-x,阻力f=-W 周期性外力Hcos(o1),o':外力频率,H:外力的幅度 d'x ma=m d? =-kx-yV+H cos(@'t) d'xrdxkx=H +二x=兰cos(o't) dr mdt mm 令义=2B,m =00, H=h m d'x +2B血+ox=heos0一—受迫振动微分方程 dt x=Aoe cos(ot+p)+A'cos(o't+) @=og-B2 t较大时,x=Acos(o1+p),简谐振动 振动颜率=强迫力的频率 h A'= V(@-o2)2+4B2o2 80'= 2Bo 0-02 4
4 0 2 2 + + x = m k dt dx dt m d x 令 0 k / m = :固有频率, / m = 2 , 0 :阻尼因子 2 0 2 2 0 2 + + x = dt dx dt d x ——阻尼振动微分方程 1、小阻尼(欠阻尼) 0 x cos( ) 0 = + − x A e t t t A A e − = 0 2 2 = 0 − , t A A e − = 0 O t 0 0 0 2 2 0 2 2 2 T = T − = = ,振动能量 ,准周期运动 2、过阻尼和临界阻尼 x 过阻尼 0 临 过 t x c e ( ) 1 2 0 2 − + − = t c e ( ) 2 2 0 2 − − − + 临界阻尼 =0 , t x c c t e − = ( + ) 1 2 二、受迫振动 周期性外力:强迫力,受迫振动 弹簧振子,弹力 F = −kx ,阻力 f = −V 周期性外力 H cos(t) , :外力频率, H :外力的幅度 cos( ) 2 2 k x V H t dt d x ma = m = − − + cos( ) 2 2 t m H x m k dt dx dt m d x + + = 令 = 2 m , =0 m k , h m H = 2 cos( ) 2 2 0 2 x h t dt dx dt d x + + = ——受迫振动微分方程 cos( ) 0 = + − x A e t t + Acos(t +) 2 2 = 0 − t 较大时, x = Acos(t +) ,简谐振动 振动频率=强迫力的频率 x 2 2 2 2 2 (0 − ) + 4 = h A 2 2 0 2 − tg = − t t

三、共振 dA' =0→0'=V06-2B2时 在周期性外力 do' 作用下,振幅 h 达到极大值的 2BV0i-B 现象称为共振 0'=√o-2B2:共振条件 B→0,共振条件o'→0,0'=00,'→0 外力对系统输入能量,系统因阻尼而损耗能量,稳定状态下, 在一个周期内,外力的功和阻力的功恰好相抵消,这正是系统 维持等幅振动的原因 当B→0,o'→0。时,外力和速度总是同方向,外力对系统 总是作正功,系统能量个(B→0),振幅个,形成共振 例:取质点向右运动通过A时开始 计时(t=0),经过2s后,质 点第一次通过B点,再经过2s 第二次通过B点,已知质点 通过AB两点时速率相同,AB=10cm 求:(1)振动方程(2)Ψ=? 解:(1)Y=Ψ,平衡位置在AB 中点,A>5cm △tAo=△toB=ls BC x △tBc=AtcB=ls △M4D=△tDA=ls,T=8s △MA=△14o,p=5π/4,A=5V2cm ()52o 4)em 2)r55.(✉+.1=0,pm 例:均质细杆(1,m),弹簧k 求:振动周期 解:重力mg向下 0较小时,弹力F=klsin0向右 取顺时针为正 mg 3mr dg M--mgsin 0-klsin 0.Icos=I=m 0较小时,sin0≈0,cos0≈1 d20,3mg+60=0 2ml 5
5 三、共振 A = 0 d dA 2 2 = 0 − 2 时 2 2 0 max 2 − = h A 2 2 = 0 − 2 :共振条件 → 0 ,共振条件 →0 , =0 , A → 外力对系统输入能量,系统因阻尼而损耗能量,稳定状态下, 在一个周期内,外力的功和阻力的功恰好相抵消,这正是系统 维持等幅振动的原因 当 → 0, →0 时,外力和速度总是同方向,外力对系统 总是作正功,系统能量 ( → 0 ),振幅 ,形成共振 例:取质点向右运动通过 A 时开始 计时( t = 0 ),经过 2s 后,质 点第一次通过 B 点,再经过 2s A B x 第二次通过 B 点,已知质点 通过 AB 两点时速率相同,AB=10cm 求:(1)振动方程(2) VA =? 解:(1) VA = VB ,平衡位置在 AB 中点, A 5cm t t s AO = OB =1 D A O B C x t t s BC = CB =1 t t s AD = DA =1 ,T = 8s DA AO t = t , = 5 / 4, A = 5 2cm x t t )cm 4 5 4 ( ) 5 2 cos( = + (2) ) 4 5 4 )sin( 4 5 2 ( V = − t + , t = 0, VA = cm / s 4 5 O 例:均质细杆( l,m ),弹簧 k 求:振动周期 l 解:重力 mg 向下 k F 较小时,弹力 F = klsin 向右 取顺时针为正 mg 2 2 2 3 1 sin sin cos 2 dt d k l l I ml l M mg = − − = = 较小时, sin ,cos 1 0 2 3 6 2 2 = + + ml mg kl dt d 在周期性外力 作用下,振幅 达到极大值的 现象称为共振

3mg +6kl T 2元-2r 2ml 0= 2ml 0 3mg +6kl 例:将一根弹簧(k)从中间一分为二,每一部分K'=? 串联 k kz k+k2 并联 ·-w k 例:电梯匀加速a上升 求:弹簧振子系统的T 解:以电梯为参考系,惯性力ma m ↑a 静止形变6t,mg+ma=kδ F 重力mg,惯性力ma 弹力F=-k(⑥,+x) ma mg d'x mg+ma-k(δ+x)=m dr d'x k kx=0,0=\m ”与电梯的加速度无关 6
6 ml mg kl 2 3 + 6 = , mg kl ml T 3 6 2 2 2 + = = 例:将一根弹簧( k )从中间一分为二,每一部分 k = ? 串联 1 k 2 k 1 2 1 2 k k k k k + = 1 k 1 k 2 k 并联 1 2 k = k + k 2 k 例:电梯匀加速 a 上升 求:弹簧振子系统的 T 解:以电梯为参考系,惯性力 ma m O a 静止形变 st , st mg + ma = k F 重力 mg ,惯性力 ma x 弹力 F k( x) = − st + ma mg 2 2 ( ) dt d x mg + ma − k st + x = m x 0 2 2 + x = m k dt d x , m k = k m T 2 2 = = 与电梯的加速度无关