
§3.3电子的自旋 ·光谱和能级的精细结构应该从原子的运动 特征进行解释 1.轨道磁矩 原子中的核外电子,由于具有角动量,而 产生磁矩 电子由于绕原子核运动的角动量p,产生轨 道磁矩1
§3.3 电子的自旋 • 光谱和能级的精细结构应该从原子的运动 特征进行解释 • 原子中的核外电子,由于具有角动量,而 产生磁矩 • 电子由于绕原子核运动的角动量pl,产生轨 道磁矩μl 1. 轨道磁矩

单电子原子的轨道磁矩 ·磁矩的方向与角动量的方向相反 ·轨道角动量分别绕总角动量旋进(进 动),相应的磁矩也绕总角动量旋进 (进动) e-1 2me
单电子原子的轨道磁矩 • 磁矩的方向与角动量的方向相反 • 轨道角动量分别绕总角动量旋进(进 动),相应的磁矩也绕总角动量旋进 (进动) e 2 l e m μ l

为使磁矩与角动量间有统一的关系式 ·引入Landè因子g e 2m.D 2m P Lande g因子 轨道g因子 8=1
为使磁矩与角动量间有统一的关系式 • 引入Landè因子g e 2 l l e m μ p 1 l g e 2 l l e g m p Landè g因子 轨道g因子

外磁场中的原子 ·外磁场中的磁矩 有磁矩的原子在外磁场中,受到力和力矩 的作用F=V(u·B)T=M×B B de=wdt A、力矩的作用,使得角动量P +dp 绕外磁场B旋进(进动),这种 进动称作Larmori进动 dP=Psin Bde dP=Psin B d=Psin Bo dt dt 可以用矢量式表示 =ωXP=T=W×B
外磁场中的原子 • 外磁场中的磁矩 • 有磁矩的原子在外磁场中,受到力和力矩 的作用 F ( ) μ B Γ μ B A、力矩的作用,使得角动量P 绕外磁场B旋进(进动),这种 进动称作Larmor进动 P P P d dP d d t d sin d P P d dt P ω P μ B d d sin d d P P t t Psin 可以用矢量式表示 Γ μ B

4= p epi eh Pr h 二一 轨道回磁比 2me 2me 2me 1 MB B MePi B h p=wxp,=4×B p1×B= eB ×卫1 2me 2me eB 41 0= 2me 轨道角动量的Lamori进动
e 2 l l ep m e 2 l l e m p μ e 2 B e m B l l p μ d d l l t p ω p μl B e 2 l e m p B e 2 l e m B p e 2 e m B ω l p B z μl z 轨道角动量的Lamor进动 l p B μl l l B p μ 轨道回磁比

外磁场对原子的作用力 ·有磁矩的原子在外磁场中,受到力的作用 U=-u·B F=-VU=V(·B) uB=uB.+u,B.+u.B. V(4,B+4,B,+4B:)=4:Ox By OBseuy oy ,+4:az 在均匀的外磁场中,由于 OB, aB:二0 8x 0z F=V(W·B)=0但是,力矩却不等于零 拉莫尔进动(Larmor precession)
外磁场对原子的作用力 • 有磁矩的原子在外磁场中,受到力的作用 F U ( ) μ B μ B x x y y z z B B B ( ) x y z x x y y z z x x y y z z B B B B B B x y z e e e 0 x y z y B B B x y z F ( ) 0 μ B B μ 在均匀的外磁场中,由于 但是,力矩却不等于零 拉莫尔进动(Larmor precession) U μ B

2 Zeeman效应(1896年) ·一、现象 磁场中,光谱线发生分裂,原来的一条 谱线分裂为多条,且均为偏振光。 D, D S Na:5896ANa:5890A 2Pn→2Sn2Pn→2Sn 品 Na原子1s22s22p63s
2 Zeeman效应(1896年) • 一、现象 • 磁场中,光谱线发生分裂,原来的一条 谱线分裂为多条,且均为偏振光。 B N S Na:5896A Na:5890A 2 2 P S 1/2 1/2 2 2 P S 3/2 1/2 D2 D1 2 2 6 1 Na原子 1s 2s 2p 3s 2 S1/2 2 P1/ 2 2 P3/ 2 D2 D1

D D

逆着磁场方向观察 右旋σ 左旋o 中 垂直于磁场方向观察 有磁场 π B oππσ 无磁场 左旋 中 右旋
左旋 右旋 j j 无磁场 有磁场 N S B 逆着磁场方向观察 垂直于磁场方向观察 左旋 右旋
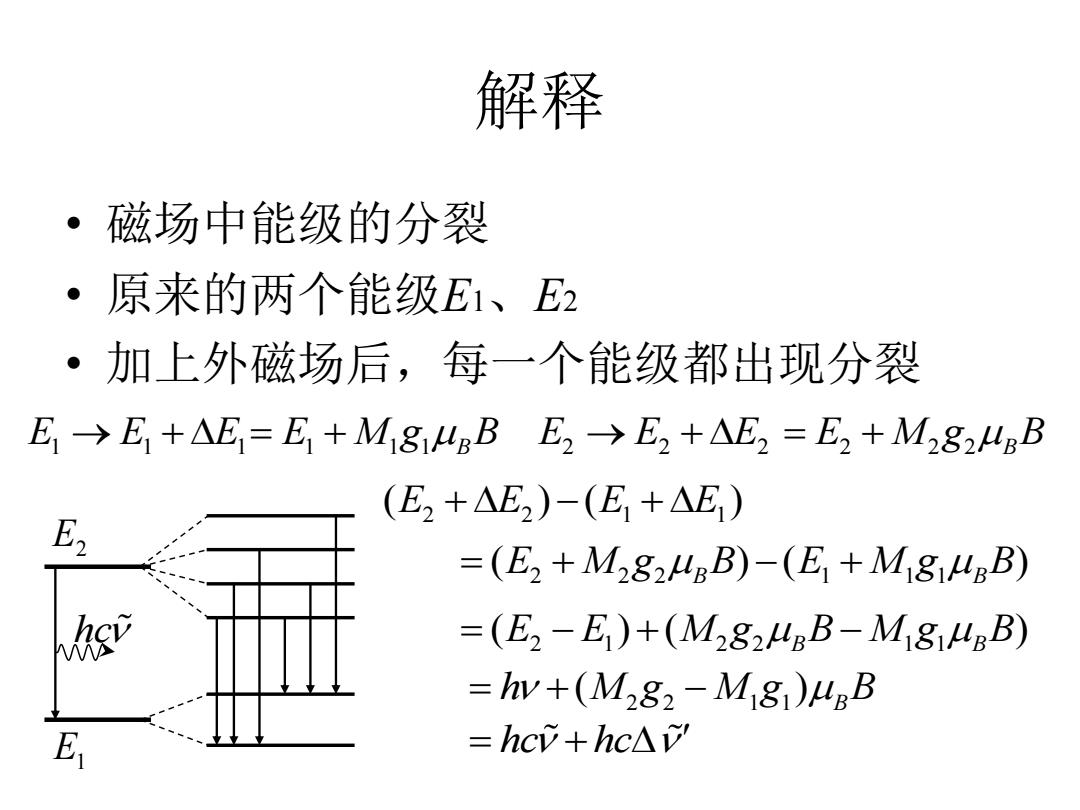
解释 ·磁场中能级的分裂 ·原来的两个能级E1、E2 ·加上外磁场后,每一个能级都出现分裂 E>E+E=E+Mi8 ugB E2>E2+AE?=E2+M282lgB (E2+△E2)-(E,+△E) E2 =(E2+M2824BB)-(E1+M1814BB) =(E2-E)+(M2824BB-M1814BB) =hw+(M282-M181)'aB E =hcv+hc△
解释 • 磁场中能级的分裂 • 原来的两个能级E1、E2 • 加上外磁场后,每一个能级都出现分裂 E E E 1 1 1 E E E 2 2 2 2 2 1 1 ( ) ( ) E E E E 2 2 2 1 1 1 ( ) ( ) E M g B E M g B B B 2 1 2 2 1 1 ( ) ( ) E E M g B M g B B B 2 2 1 1 ( ) B h M g M g B E1 E2 hc hc E M g B 1 1 1 B E M g B 2 2 2 B hc