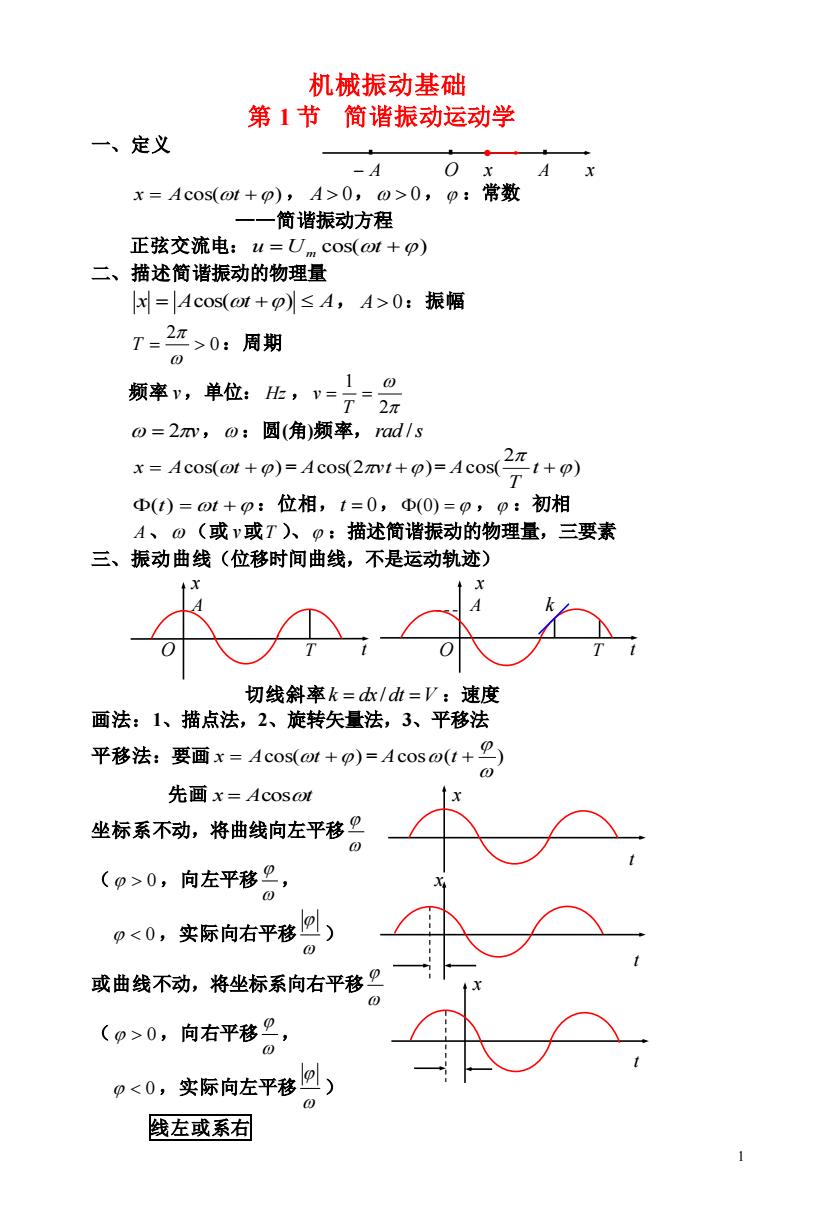
机械振动基础 第1节简谐振动运动学 一、定义 -A A x=Ac0s(ot+p),A>0,0>0,0:常数 一一简谐振动方程 正弦交流电:u=U cos(ot+p) 二、描述简谐振动的物理量 =Acos(ot+p≤A,A>0:振幅 T=27>0:周期 0 频率,单位:伦,行元 0=2,0:圆(角)频率,ad/s 2π x=Acos(o+)=Acos(2+)=Acos(+) Φ(t)=ot+p:位相,t=0,Φ(0)=p,p:初相 A、⊙(或v或T)、p:描述简谐振动的物理量,三要素 三、振动曲线(位移时间曲线,不是运动轨迹) 切线斜率k=dk/d=V:速度 画法:1、描点法,2、旋转矢量法,3、平移法 平移法:要画x=Acos(or+p)=Acoso(t+2) 先画x=Acos@t 坐标系不动,将曲线向左平移巴 (p>0,向左平移2, 0 p0,向右平移2, 0 p<0, 实际向左平移回) 饯左或系右
1 机械振动基础 第 1 节 简谐振动运动学 一、定义 − A O x A x x = Acos(t +) , A 0, 0, :常数 ——简谐振动方程 正弦交流电: u = U cos(t +) m 二、描述简谐振动的物理量 x = Acos(t +) A, A 0 :振幅 0 2 = T :周期 频率 v ,单位: Hz , 2 1 = = T v = 2v, :圆(角)频率, rad /s x = Acos(t +) = Acos(2vt +)= ) 2 cos( t + T A (t) = t + :位相, t = 0,(0) = , :初相 A、 (或 v 或 T )、 :描述简谐振动的物理量,三要素 三、振动曲线(位移时间曲线,不是运动轨迹) x x A A k O T t O T t 切线斜率 k = dx / dt =V :速度 画法:1、描点法,2、旋转矢量法,3、平移法 平移法:要画 x = Acos(t +) = cos ( ) A t + 先画 x = Acost x 坐标系不动,将曲线向左平移 ( 0,向左平移 , x 0 ,实际向右平移 ) 或曲线不动,将坐标系向右平移 x ( 0,向右平移 , 0 ,实际向左平移 ) 线左或系右 t t t

四、周期、位相的进一步讨论 1。-t。=T 46-l。≠T Φ。-Φ =(otc+)-(ota+) =o(tc-ta)=oT=2π 任意时刻t一确定的运动状态(振动状态) 台确定的位相Φ=ot+p 位相是决定质点振动状态的物理量 注意与“A、0、p是描述简谐振动的物理量”的区别 五、谐振质点的速度和加速度 位移 x=Acos(ot+) 速度 v=dx =-OAsim(ot+), dt 加速度a= dv =-@2Acos(ot+p),dms =02A dt 六、谐振微分方程 a=d业、d2x dt di =-02Ac0s(ot+p)=-02x d山+0x=0一一谐振徽分方程 d-x d20,1 h+1c0=0 1 0= √iC 注意:谐振微分方程中因变量前的系数是大于零的常数 七、超前、滞后、同相、反相 两个同频率的简谐振动x1=Acos(a1+p) x2=A cos(ot+2) Φ2-Φ1=(0t+p2)-(ot+p1)=p2-p,=△p △p=p2-p,>0,2比1超前△p △0=p2-p1<0,2比1滞后△p △0=p2-9,=±2kπ,=0,12…,同相 △0=p2-p=±(2k+1)π,k=0,1,2…,反相 x=Acos(ot+p) V--m4si+)-Qdcos(+ a=-@2Acos(ot+p)=@2Acos(ot+p+) v比x超前,a比v超前?,a与x反相 2
2 四、周期、位相的进一步讨论 x t c − t a = T a b c t b − t a T c −a O a t b t c t t = ( +) −( +) c a t t = ( ) c a t − t =T = 2 任意时刻 t 确定的运动状态(振动状态) 确定的位相 =t + 位相是决定质点振动状态的物理量 注意与“ A 、 、 是描述简谐振动的物理量”的区别 五、谐振质点的速度和加速度 位移 x = Acos(t +) 速度 = = −Asin(t +) dt dx V , Vmax =A 加速度 cos( ) 2 = = − A t + dt dV a , a A 2 max = 六、谐振微分方程 A t x dt d x dt dV a 2 2 2 2 = = = − cos( +) = − 0 2 2 2 + x = dt d x ——谐振微分方程 0 1 2 2 + Q = dt LC d Q L C LC 1 = 注意:谐振微分方程中因变量前的系数是大于零的常数 七、超前、滞后、同相、反相 两个同频率的简谐振动 cos( ) 1 = 1 +1 x A t cos( ) 2 = 2 +2 x A t ( ) ( ) 2 −1 = +2 − +1 t t = 2 −1= = 2 −1 0,2 比 1 超前 = 2 −1 0,2 比 1 滞后 = 2 −1= 2k , k = 0,1,2 ,同相 = 2 −1= (2k +1) , k = 0,1,2 ,反相 x = Acos(t +) ) 2 sin( ) cos( V = −A t + =A t + + cos( ) cos( ) 2 2 a = − A t + = A t + + V 比 x 超前 2 ,a 比 V 超前 2 ,a 与 x 反相 − Q Q

八、简谐振动的旋转矢量表示法 x =Acos(ot+) A:振幅矢量 t=0 参考圆 振幅A:A的长度 O:A旋转的角速度 p:t=0,A与x轴正向的夹角 本=o1+p:任意时刻t,A与x轴正向的夹角 x=Acos(ot+p):A的末端点在x轴上的投影坐标 OA x=AcoSot t0 A】 t=T/4 t=3/4 14 t=T/2 九、A、0与初条件的关系 x Acos(ot+p),V=-@Asin(ot+) t=0,xo=Acoso,Vo=-@Asin ,cosp=或g二与 4=+ y x>0,'。>0,peIV x。>0,'。0,peIΠ x<0,V。<0,p∈II 三要素中A、p由初条件决定 0由振动系统决定,与初条件无关 3
3 八、简谐振动的旋转矢量表示法 x = Acos(t +) t A :振幅矢量 A , t = 0 参考圆 t 振幅 A : A 的长度 O x x : A 旋转的角速度 : t = 0, A 与 x 轴正向的夹角 =t + :任意时刻 t , A 与 x 轴正向的夹角 x = Acos(t +) : A 的末端点在 x 轴上的投影坐标 A A O x A 2 x x = Acost t = 0 A A t =T /4 t = 3T /4 O O T / 4 T / 2 3T / 4 T t t =T /2 九、 A、 与初条件的关系 x = Acos(t +) ,V = −Asin(t +) t = 0, x0 = Acos ,V0 = −Asin 2 2 2 0 0 V A = x + , A x0 cos = 或 0 0 x V tg = − A x x A x0 0,V0 0 , V x0 0 ,V0 0 , A x x A x0 0 ,V0 0 , x0 0,V0 0 , 三要素中 A 、 由初条件决定 由振动系统决定,与初条件无关

十、振动曲线一振动方程(A、0、p),cos0=/A 例:振幅0.12m,周期2s,仁0,x。=0.06m,沿x轴正向运动 求:(1)p(2)=0.5s,x,V,a (3)从x=-0.06m且沿x轴负向运动到x=0,△t=? (4)物体在平衡位置且沿x轴负向运动开始计时 求初相和运动方程 解:(1)A=0.12m,T-2s x=Acos( 271+p)=0.12cos(m+p)(m t0,x。=0.06=0.12cosp,cosp=1/2 x>0,'。>0,p∈IV,p=-π/3或5π/3 (2)=0.12cos(m-3Xm),r=-012xsm-3ms a=-0.12x2co(m-3)m/s2 t=0.5s,x=0.104(m),V=-0.19m/s,a=-1.03m/s2 (3) (4)0 0 X ○ △Φ=π+刀-5 ,0=π 326 0=。 2 △1=△Φ/0=2s 6 =0.12com+7(m) 例:由振动曲线写振动方程 tx (cm) t(s) -21 解:A=2cm,x=2cos(ot+p) x0=-1=2c0sp,c0sp=-1/2 x<0,'<0,p∈IⅡ,p=2π/3 0=4π/3x=2c0s( +2(cm) 33 4
4 十、振动曲线 振动方程 ( A 、 、 ), cos = x0 / A A 0 x t 例:振幅 0.12m,周期 2s,t=0, 0 x =0.06m,沿 x 轴正向运动 求:(1) (2)t=0.5s,x,V,a (3)从 x= −0.06m 且沿 x 轴负向运动到 x=0,t = ? (4)物体在平衡位置且沿 x 轴负向运动开始计时 求初相和运动方程 解:(1)A=0.12m,T=2s ) 2 cos( = t + T x A = 0.12cos(t +) (m) t=0, 0 x =0.06= 0.12cos , cos = 1/2 x0 0,V0 0 , V, = − /3或5 /3 (2)x= )( ) 3 0.12cos( t m − , ) 3 0.12 sin( V = − t − m/s ) 3 0.12 cos( 2 a = − t − 2 m / s t=0.5s,x=0.104(m),V = −0.19 m/s , a = −1.03 2 m / s (3) A (4) O x O x 6 5 3 2 = + = , = 2 = t s 6 5 = / = x= ) 2 0.12cos( t + (m) 例:由振动曲线写振动方程 x (cm) -1, 1 t(s) O x -2 解: A = 2cm, x = 2cos(t +) x0 = −1 = 2cos , cos = −1/ 2 x0 0 ,V0 0 , , = 2 / 3 = 4 /3 )( ) 3 2 3 4 x 2cos( t cm = + A A x