西安电子科技大学：《大学物理》课程教学讲义（上）10 刚体定轴转动定律

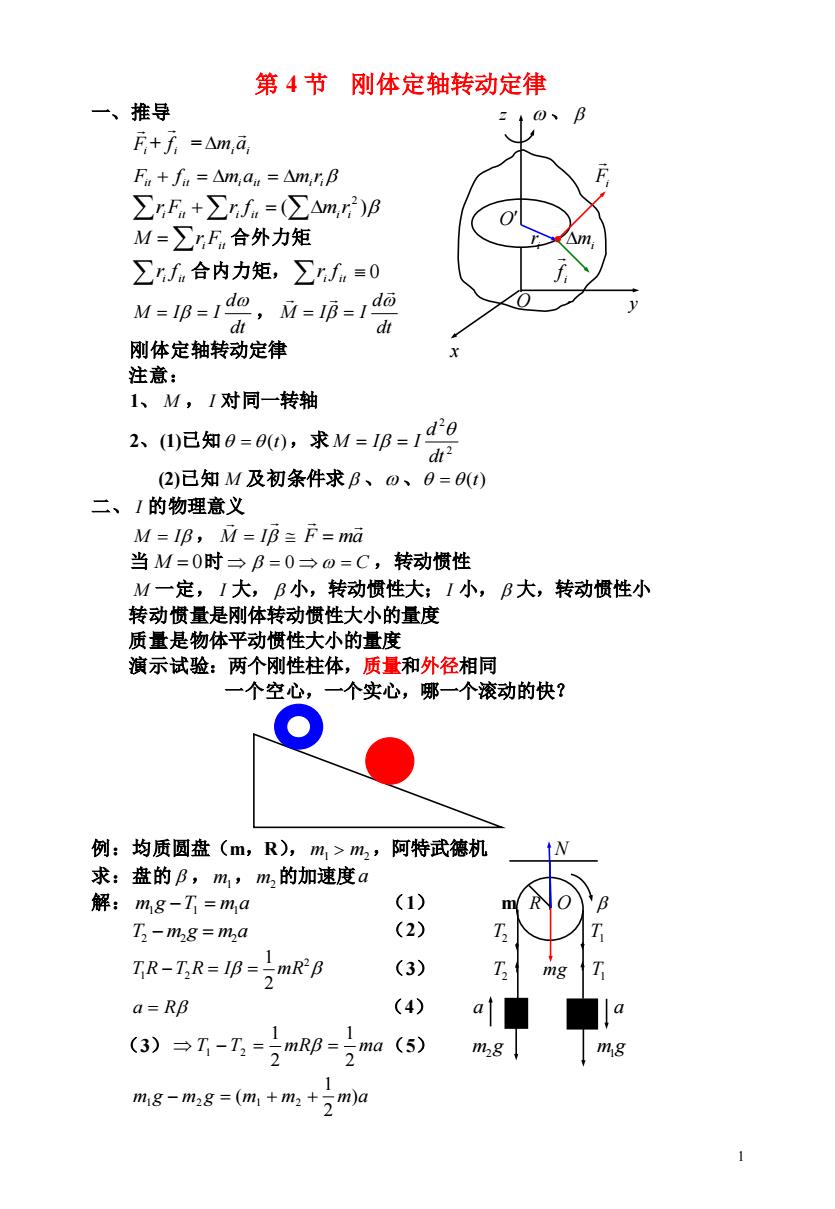
第4节刚体定轴转动定律 一、推导 t、 B F+f=△m,a, Fn+fa=△m,aa=△m,5B ∑rEn+∑=（∑Awm,2)p M=∑rE,合外力矩 ∑fn合内力矩，∑fn=0 M=B=1安，M== dt 刚体定轴转动定律 注意： 1、M,I对同一转轴 2已知0=00)，求M=B=1d0 d (2)已知M及初条件求B、0、0=() 二、1的物理意义 M=IB,M=I邛=F=ma 当M=0时三B=0一0=C,转动惯性 M一定，I大，B小，转动惯性大；I小，B大，转动惯性小 转动惯量是刚体转动惯性大小的量度 质量是物体平动惯性大小的量度 演示试验：两个刚性柱体，质量和外径相同 一个空心，一个实心，哪一个滚动的快？ 例：均质圆盘(m,R),m,>m2,阿特武德机 求：盘的B，m，m2的加速度a 解：mg-T=ma (1) T3-m28=%a (2) TR-TR=IB--mRB (3) mg a=Rβ (4) ③)→1-，mR6=ma(⑤ m28 mg m18-m28=(m1+m2+-m)a 1

1 第 4 节 刚体定轴转动定律 一、推导 z  、  Fi  + i f  = miai   Fit + f it = miait = mi ri Fi   + = ( ) 2 i it i it i i r F r f m r =  iFit M r 合外力矩 i r mi  i it r f 合内力矩，  i it r f  0 i f  dt d M I I  =  = ， dt d M I I      = = 刚体定轴转动定律 x 注意： 1、 M ， I 对同一转轴 2、(1)已知  =  (t) ，求 2 2 dt d M I I  =  = (2)已知 M 及初条件求  、 、 =  (t) 二、 I 的物理意义 M = I ，    M = I  F ma   = 当 M = 0 时   = 0   = C ，转动惯性 M 一定， I 大，  小，转动惯性大； I 小，  大，转动惯性小 转动惯量是刚体转动惯性大小的量度 质量是物体平动惯性大小的量度 演示试验：两个刚性柱体，质量和外径相同 一个空心，一个实心，哪一个滚动的快？ 例：均质圆盘（m，R）， m1  m2 ，阿特武德机 N 求：盘的  ， m1，m2 的加速度 a 解： m1g −T1 = m1a （1） m R O  T2 − m2g = m2a （2） T2 T1   2 1 2 2 1 T R −T R = I = mR （3） T2 mg T1 a = R （4） a a （3） T T mR ma 2 1 2 1  1 − 2 =  = （5） m2g m g1 m g m g m m m)a 2 1 ( 1 − 2 = 1 + 2 + O O y

a=m-m 318,B=9=m-m,8 R 1 R m+ma m+ma2m 讨论：(1)若滑轮质量m=0,a=m二mg,T=工 m1+m2 (2)考虑轴承摩擦 TR-TR-M=IB (3)若顺时针有一主动力矩 M:+TR-TR-M=IB 例：均质杆(1，m)可绕其一端N八9 的水平轴在竖直平面内转动 01 求：杆由水平位置无初速释放转过 1/2 0角时的B及⊙ 解：M=mgcos0,1=m mg 0、B 2 M=I8,mgicose=ImPB 1 3 B、 cos0 21 B=do=3g coso,do do3g cos0 d21 d0d21 joxdo-j 3 osino 12 2 -cosede, 2 27 @=3gsin0/1 第5节刚体定轴转动中的功和能 一、力矩的功 z0 dt dA=F.dr=Fcosads Fcosa=F dA=Frde Mde 0→02 A=∫h=Ma0 如果刚体同时受几个力E,E,,F作用 dA=dA+…+dA =Md0+…+Mnd0=(M1+…+Mn)d0=Mdθ 说明：（①力矩的功就是力的功 2功率P=4-0=MO dt dt 2

2 g m m m m m a 2 1 1 2 1 2 + + − = ， = = R a  R g m m m m m 2 1 1 2 1 2 + + − 讨论：（1）若滑轮质量 m = 0， g m m m m a 1 2 1 2 + − = ，T1 = T2 （2）考虑轴承摩擦 T1R −T2R − M f = I （3）若顺时针有一主动力矩 M主 + T1R −T2R − M f = I 例：均质杆（ l，m ）可绕其一端 O m l 的水平轴在竖直平面内转动  求：杆由水平位置无初速释放转过 l / 2  角时的  及  解： cos 2 l M = mg ， 2 3 1 I = ml mg  、  M = I ， cos 2 l mg =  2 3 1 ml  cos 2 3 l g =    cos 2 3 l g dt d = = ，     cos 2 3 l g dt d d d =   =       0 0 cos 2 3 d l g d ，  sin  2 3 2 1 2 l g =  = 3g sin /l 第 5 节 刚体定轴转动中的功和能 一、力矩的功 z  dt F  dA = F  dr = F cosds   F  = Ft cos O d  dA = Ft rd = Md r  dr  1 → 2 O y   = = 2 1   A dA Md x 如果刚体同时受几个力 F F Fn     , , , 1 2 作用 M d M d M M d Md dA dA dA n n n = + + = + + = = + + ( ) 1 1 1    说明：(1)力矩的功就是力的功 (2)功率   M dt Md dt dA P = = = A ds N

二、刚体的转动动能 1 E=∑m=∑4mro-1o 2 三、刚体定轴转动动能定理 合外力矩M,dt,d0 dA外-Md0=lRu0=Id odt dt lodo=d(lo2)=dEg d4外=dE:动能定理（微分形式） A外=△E4:动能定理（积分形式） 注意：质点系：A外+A内=△E,A内≠0 刚体：A内=「M内d0=0,A外=△E 四、刚体的重力势能=全部质量集中在质心时的重力势能 对于刚体或包括刚体的系统， 若只有保守内力作功，机械能守恒 例：求杆由水平位置无初速释放 转过0角时的0 解：（一)：机械能守恒 1/2 O:重力势能零点 0-)1o2+←mg2sn0), mg 11 ml2o2 =mgsin 0,=3gsin0/1 23 解：（二)：动能定理 1-∫B-mg5cos0=ms5a0=a,=o同上 0 例：均质圆盘(M、R)可 绕水平轴无摩擦转动 入RM 求：物体m下降h时的速度 解：mgh=m )22+11MR2o2,V=oR 22 1 4mgh G5m+aM0w,V=M+2m】 3

3 二、刚体的转动动能 z  2 2 2 2 1 2 1 miVi = mi ri  =   =   = 2 2 2 2 2 1 2 1 2 1 Ek miVi mi ri  I Vi  三、刚体定轴转动动能定理 i r mi 合外力矩 M ， dt ，d dt dt d dA Md I d I   =  =   = 外 dEk = I d = d I ) = 2 1 ( 2    dA = dEk 外 ：动能定理（微分形式） A = Ek 外 ：动能定理（积分形式） 注意：质点系： A + A = Ek 外 内 ，  0 内A 刚体： 内A =  M d = 0 内 ， A = Ek 外 四、刚体的重力势能=全部质量集中在质心时的重力势能 对于刚体或包括刚体的系统， 若只有保守内力作功，机械能守恒 例：求杆由水平位置无初速释放 O m l 转过  角时的   解：（一）：机械能守恒 l / 2 O ：重力势能零点 0= sin ) 2 ( 2 1 2   l I + −mg ， mg   sin  3 2 1 2 1 2 2 l  ml = mg ， = 3g sin /l 解：（二）：动能定理   = = = =  =        0 0 2 2 1 sin 2 cos 2 E I l d mg l A Md mg k 同上 例：均质圆盘（ M 、 R ）可 绕水平轴无摩擦转动  R M 求：物体 m 下降 h 时的速度 O m h V 解： 2 2 2 2 1 2 1 2 1 mgh = mV + MR  ，V =R = 2 ) 4 1 2 1 ( m + M V ， M m mgh V 2 4 + = O O y x N