
§2.2 Schrodinger方程 o Schrodinger方程是量子力学的最基本方程 ·不是经过严格的推导而获得的 ·是用试探方法找到的 ·或者说是“猜”到的 ·自由粒子,或者单色平面波的波函数 (x,t)=wo ei(kx)=Wop x=(xex,yev,ze)位矢 k=(kex,kev,ke)波矢 P=(pex,Pey,P.e)动量
§2.2 Schrödinger方程 • Schrödinger方程是量子力学的最基本方程 • 不是经过严格的推导而获得的 • 是用试探方法找到的 • 或者说是“猜”到的 • 自由粒子,或者单色平面波的波函数 ( ) ( )/ 0 0 ( , ) e e i t i Et t k x p x x ( , , ) x y z x e e e x y z ( , , ) x x y y z z k e e e k k k ( , , ) x x y y z z p e e e p p p 位矢 波矢 动量

(化,t)=4ekx-o)=yoep-/i E=加=么2v= p21 hh2π 二hk 2π 2π元 Agt0a2心=awx=Bx Ot Ot ow(x.t)_-inwo Ox =放wx,nwx Ox -h2(-)-hw化》p=ix Ox &x ex *0
( ) ( )/ 0 0 ( , ) i t i Et t e e k x p x x 2 2 h h p k 2 2 h E h ( , )t i t x ( , )t i x x i i ( ) x x 2 2 2 2 ( , ) ( , ) x t p t x x x ( ) 0 i t e i t k x ( , ) x t E t ( , ) x ( ) 0 i t e i x k x ( , ) x k t x ( , ) x p t x ( , ) x t i p x x 2 ( , ) x p t x

-r)=piw(xt) -答0=ixn -ig+n-+p+p小 vwcx小-x0=0 2m ow(D)=Ew(x)=Ew(x.t) 自由粒子E=E Ot h ov(x,t) Ot v2wx,) 2m 自由粒子的Schrodinger方程
2 2 2 2 ( , ) ( , ) y t p t y x x 2 2 2 2 2 2 2 [ ] ( , )t x y z x 2 2 2 ( , ) ( , ) 2 2 p t t m m x x 2 2 ( , ) ( , ) 2 t i t t m x x ( , ) ( , ) t i E t t x x 2 2 2 2 ( , ) ( , ) z t p t z x x 222 [ ] ( , ) x y z p p p t x ( , ) E t k x 自由粒子的Schrödinger方程 ( , ) E t k x 自由粒子 E E k

自由粒子访 0w(x,t)_ 8t Vy(x,) 2m 对于处于势场中的粒子,除了动能,还有势能 =+人:分 Hamilton量 2m ow(x,t) V+V() 8t 2m a E→h p->-ihv 8t →- 2m 力学量算符 v2+V(x,) Hamilton算符 2m
2 2 ( , ) ( , ) 2 t i t t m x x E E E k p ( , )t i t x E i t p i 对于处于势场中的粒子,除了动能,还有势能 2 2 ( , ) 2 V t m x Hamilton算符 Hamilton量 自由粒子 2 ( , ) 2 p V t m x 2 2 [ ( , )] ( , ) 2 V t t m x x 力学量算符 2 2 2 Ek m

i清OwxD-[-v+VGx.DMx,0 Ot 2m 对于定态势能场 V(x,t)=V(x) 分离变量w(x,t)=w(x)f(t) 访 (D, dt ux)=2Vx)+e必o0 1 df(t) 1 f(t)dt cw四 访1 df()-E f(t)dt f(t)=Ce-iEuln V(() 定态Schrodinger方程 Hamilton方程 方程的解 v(x,t)=v(x)e
( , ) ( ) ( ) x x t f t 2 d ( ) 2 ( ) [ ( ) ( ) ( )] ( ) d 2 f t i V f t t m x x x x 2 1 d ( ) 1 2 [ ( ) ( ) ( )] ( ) d ( ) 2 f t i V f t t m x x x x 1 d ( ) ( ) d f t i E f t t / ( ) iEt f t Ce 2 2 [ ( )] ( ) ( ) 2 V E m x x x / ( , ) ( ) iEt t e x x 对于定态势能场 定态Schrödinger方程 Hamilton方程 V t V ( , ) ( ) x x 分离变量 2 2 [ ( , )] ( , ) 2 V t t m x x ( , )t i t x 方程的解

§2.3力学量的算符 ·对波函数做某一数学运算,即用某一算符 作用于波函数,等效于用某一力学量乘以 波函数 -ih Ox =pxΨ -ihVw=p必 访 0Ψ =Ew Ot px =-ih p=-iV龙=访 Ox 8t [- V2+V(x)]w(x)=Ew(x) =X 21m E=- V(x)= (x)=V(x) 2m
§2.3 力学量的算符 • 对波函数做某一数学运算,即用某一算符 作用于波函数,等效于用某一力学量乘以 波函数 i E t i p x i p x ˆ x p i x p ˆ i E i ˆ t 2 2 [ ( )] ( ) ( ) 2 V E m x x x 2 2 ˆ ˆ ( ) 2 E V H m x x x ˆ ˆ V V ( ) ( ) x x
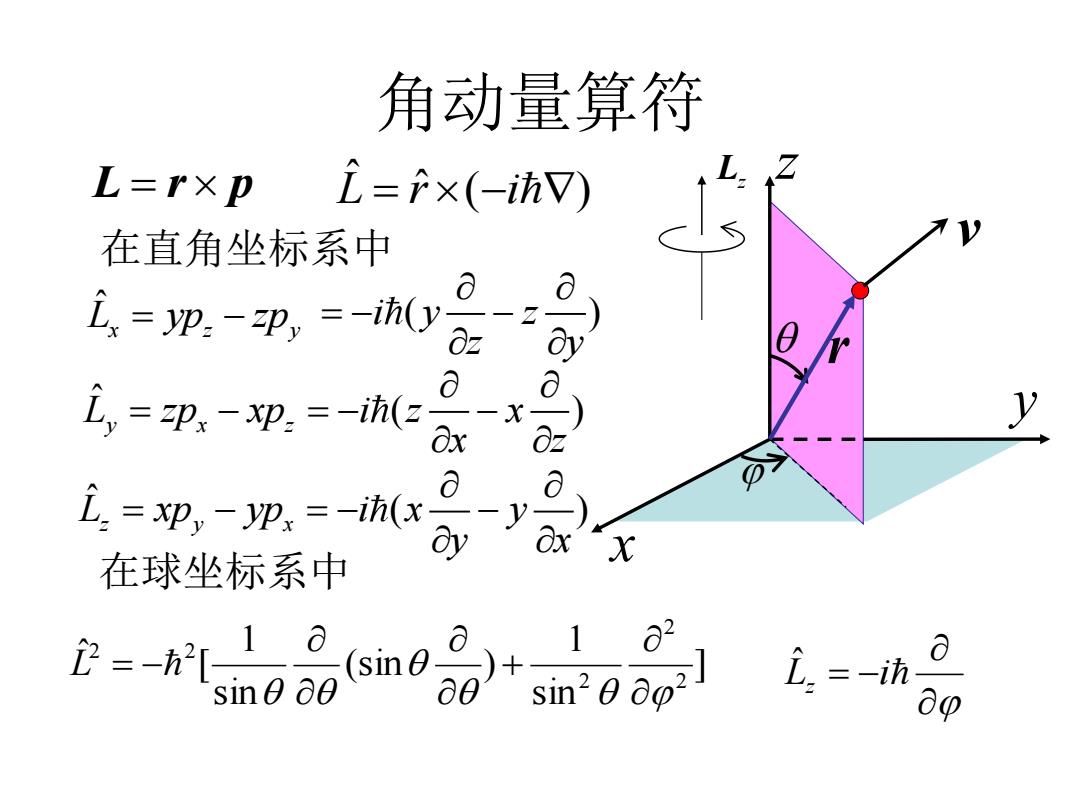
角动量算符 L=rxp i=r×(-hV) Z 在直角坐标系中 立=yp.-印,=-ih(y a 工,=印-p.=-(2 一X y &x ∂z i.=xp,-yp:=-ih(x ∂ 在球坐标系中 2-io品m0品+a] 2 D=一访
角动量算符 r v L z x y z L r p ˆ ( ) L ˆ r i ˆ L yp zp x z y ˆ ( ) L zp xp i z x y x z x z ˆ ( ) L xp yp i x y z y x y x Lz i ] ˆ sin 1 (sin ) sin 1 [ ˆ 2 2 2 2 2 L 在直角坐标系中 i y z ( ) z y 在球坐标系中

表象与力学量的平均值 x)为粒子的波函数,x)P表示粒子在x处出现 的几率,即粒子的位置值等于x的几率 则x的平均值为 xw(xdx=w(x)x(x)dx =w(x)xw(x)]dx =w(x)儿w(x)]dx 粒子的势能由其位置决定,其势能等于(x)的几 率为x)2,则x)的平均值为 F-∫V(x)川yw(x)Pdx=∫y(x)Vy(xdx =w(x)w(x)]dx
表象与力学量的平均值 • Ψ(x)为粒子的波函数,|Ψ(x)|2表示粒子在x处出现 的几率,即粒子的位置值等于x的几率 • 则x的平均值为 2 x x x x | ( ) | d ( )[ ( )]d x x x x ˆ • 粒子的势能由其位置决定,其势能等于V(x)的几 率为|Ψ(x)|2 ,则V(x)的平均值为 2 V V x x x ( ) | ( ) | d ( )[ ( )]d x V x x ( ) ( )d x x x x ( )[ ( )]d x x x x ˆ ( )[ ( )]d x V x x

。 但粒子的动量为p的几率,却不能直接用 x)描述 要计算动量p的平均值,必须知道关于p的 几率分布函数(p) ·p(p)为动量表象下的波函数,表示非单色波 中,波长值为=h/p的几率幅 ·实际就是波长为λ的单色成分的振幅 2π w(x)=∑a(2em ∑p(p)epn h
• 但粒子的动量为p的几率,却不能直接用 Ψ(x)描述 • 要计算动量p的平均值,必须知道关于p的 几率分布函数φ(p) • φ(p)为动量表象下的波函数,表示非单色波 中,波长值为λ=h/p的几率幅 • 实际就是波长为λ的单色成分的振幅 / ( ) ( )eik x x a 2 k h p / ( )eip x p

(x)为位置表象下的波函数,表示粒子(即 波包)在位置空间的几率幅(复振幅) ·波包x)为一系列振幅为p(p)的不同波长的单 色波叠加的结果 )ea∫pedp 其Fourier反变换即为动量的波函数 opD=2a肉=xedn
• Ψ(x)为位置表象下的波函数,表示粒子(即 波包)在位置空间的几率幅(复振幅) • 波包Ψ(x)为一系列振幅为φ(p)的不同波长的单 色波叠加的结果 / 3 3/ 2 1 ( ) ( )e d (2 ) i p x x p p / 3 3/ 2 1 ( ) ( )e d (2 ) i p x p x x 其Fourier反变换即为动量的波函数