
第4节 波的能量 一、波的能量密度 绳上横波 张力T 质量线密度4 xAr y(x,t)=Acos[o(t-)+o] Am=uAx,V==-odsin[o(-)+ol 8L AmnAmsn' 伸长量N-a=r+(-A=A+会- 小振幅条件下,少(波形曲线切线斜率)及其平方很小 Ox 1y2+… +爱-1+器 必Ax,I,≈7,=T △l-△x≈-( 2 0x 1y}△xT Ep=(W-Amr≈2x =Asin[o(t-+,T=uc2 Ox c r24snlou-+ml E=Lc4r02 △mo2A2sin2[ot-+p 2 E=Eg+Ep=Amo2A2 sin'[o(t-)+] 结论:(1)Ek、E,都是时间的周期函数,且E=Ep (2)E是时间的周期函数 平衡位置→最大位移处,能量↓ 最大位移处→平衡位置,能量↑ (3)能量的传播速度也是c 无限大各向同性均匀媒质也成立 △m=p△V E=Ex+Ep=pAVo2A2sin'[o(t-*)+o] 能量按度.”=行=心sno-马p 1
1 y 第 4 节 波的能量 一、波的能量密度 y t c T2 绳上横波 l 张力 T T1 质量线密度 O x x x ( , ) = cos[( − ) +] c x y x t A t m = x , = − sin[( − ) +] = c x A t t y V sin [ ( ) ] 2 1 2 1 2 2 2 2 = = − + c x E mV m A t k 伸长量 l −x= ( ) ( ) [ 1 ( ) 1] 2 2 2 − + − = + x y x y x x 小振幅条件下, x y (波形曲线切线斜率)及其平方很小 + = + + 2 1/ 2 2 ( ) 2 1 [1 ( ) ] 1 x y x y l −x x x y 2 ( ) 2 1 ,T1 T2 = T EP = (l − x)T xT x y 2 ( ) 2 1 sin[( ) ] = − + c x A t x c y , 2 T = c sin [ ( ) ] 2 1 2 2 2 2 2 = − + c x A t c E c x P = sin [ ( ) ] 2 1 2 2 2 − + c x m A t E = Ek + EP = sin [ ( ) ] 2 2 2 − + c x m A t 结论:(1) Ek 、 EP 都是时间的周期函数,且 Ek = EP (2) E 是时间的周期函数 平衡位置 → 最大位移处,能量 最大位移处 → 平衡位置,能量 (3)能量的传播速度也是 c 无限大各向同性均匀媒质也成立 m = V V E = Ek + EP = sin [ ( ) ] 2 2 2 − + c x V A t 能量密度: V E w = = sin [ ( ) ] 2 2 2 − + c x A t y
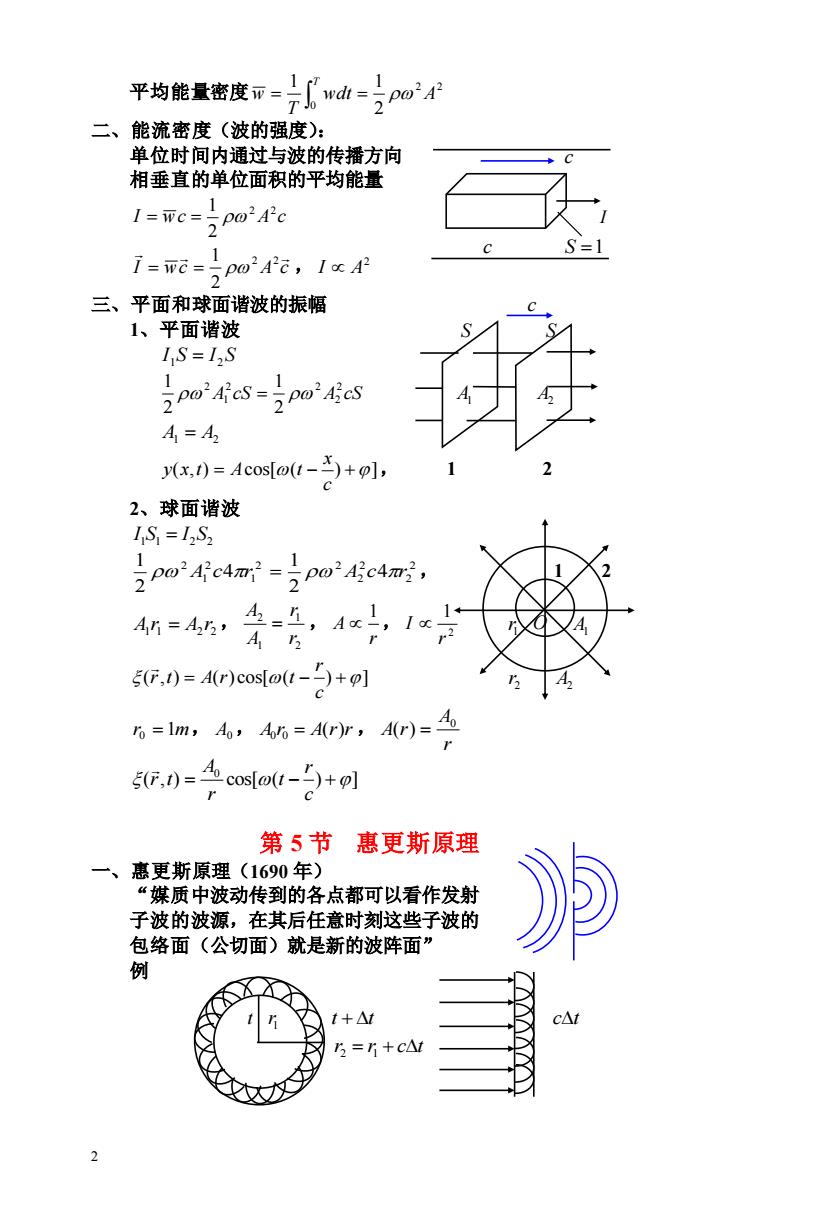
平均能量密度而=了wah=0o' 二、能流密度(波的强度): 单位时间内通过与波的传播方向 相垂直的单位面积的平均能量 I=wc=po'4'c S=1 1 1-we-p0e,I4 三、平面和球面谐波的振幅 1、平面谐波 I S=12S pniieSpo 1 A,=A2 y(x,t)Acos[o(t-)+o], 2、球面谐波 1S=12S2 20o4c4n=p043c4m, 1 4=上,Ax,1x A=AA 5G,)=4r)cos[at-5)+p] o=Im,Ao,=A(r)r,A(r)=o (.)costo(+ 第5节 惠更斯原理 一、惠更斯原理(1690年) “媒质中波动传到的各点都可以看作发射 子波的波源,在其后任意时刻这些子波的 包络面(公切面)就是新的波阵面” 例 t+△t c△ 3=i+C△1 2
2 平均能量密度 2 2 0 2 1 1 wdt A T w T = = 二、能流密度(波的强度): 单位时间内通过与波的传播方向 c 相垂直的单位面积的平均能量 I wc A c 2 2 2 1 = = I I wc A c 2 2 2 1 = = , 2 I A 三、平面和球面谐波的振幅 c 1、平面谐波 S S I 1S = I 2 S A cS A cS 2 2 2 2 1 2 2 1 2 1 = A1 A2 A1 = A2 ( , ) = cos[( − ) +] c x y x t A t , 1 2 2、球面谐波 1 1 2S2 I S = I 2 2 2 2 2 2 1 2 1 2 4 2 1 4 2 1 A c r = A c r , 1 2 1 1 2 2 A r = A r , 2 1 1 2 r r A A = , r A 1 , 2 1 r I 1 r O A1 ( , ) = ( ) cos[( − ) +] c r r t A r t 2 r A2 r0 = 1m, A0, A r A(r)r 0 0 = , r A A r 0 ( ) = ( , ) cos[ ( ) ] 0 = − + c r t r A r t 第 5 节 惠更斯原理 一、惠更斯原理(1690 年) “媒质中波动传到的各点都可以看作发射 子波的波源,在其后任意时刻这些子波的 包络面(公切面)就是新的波阵面” 例 t 1 r t + t ct r = r + ct 2 1 c S =1

二、波的绕射(衍射) 当波在传播过程中遇到障碍物时, 其传播方向会发生变化,并且能 够绕过障碍物的边缘继续向前传 播:波的绕射 波的传播方向 波的强度 X 第6节波的干涉 一、波的独立传播原理和迭加原理 当几列波在煤质中相遇时,每一列波的振幅、频率、波长、 振动方向及传播方向不因其它波的存在而受影响,或者说 每一列波都保持其独立的传播特性一波的独立传播原理 当几列波在媒质中相遇时,媒质质点的振动位移等于每列波 单独引起位移的矢量和—一波的迭加原理 二、波的干涉 1、波的干涉现象,p157 如果两列波在相遇区域迭加的结果使得某些点上振动始终加强 某些点上振动始终减弱,形成稳定的干涉花样:波的干涉现象 2、相干条件 同振向、同频率、位相差恒定一一相干条件 相干波,相干波源 3、定量分析 yio =Aio cos(ot+p) y20=A2oc0s(01+p2) y=4cos[ot-5)+0,] h2=4,cos[@t-2)+0,] y=y+2=Acos[ot-5)+0,]+4,cos[ot-2)+g,] A=VA+A+2AA,cos△0 I=1+12+2V1L2cos△p,(1cA) Ap=I@(-)+o:]-I0(t-)+o.] E02-9,-2G-)=p2二p二15-) A0=p2-0,-,巧-r):两列波在P点的位相差 3-5=6:波程差 △0=±2kπ,k=0,1,2…, A=A+A最大,I=1+2+212,干涉加强 3
3 二、波的绕射(衍射) 当波在传播过程中遇到障碍物时, 其传播方向会发生变化,并且能 够绕过障碍物的边缘继续向前传 播:波的绕射 波的传播方向 波的强度 第 6 节 波的干涉 一、波的独立传播原理和迭加原理 当几列波在媒质中相遇时,每一列波的振幅、频率、波长、 振动方向及传播方向不因其它波的存在而受影响,或者说 每一列波都保持其独立的传播特性——波的独立传播原理 当几列波在媒质中相遇时,媒质质点的振动位移等于每列波 单独引起位移的矢量和——波的迭加原理 二、波的干涉 1、波的干涉现象,p157 如果两列波在相遇区域迭加的结果使得某些点上振动始终加强 某些点上振动始终减弱,形成稳定的干涉花样:波的干涉现象 2、相干条件 同振向、同频率、位相差恒定——相干条件 相干波,相干波源 3、定量分析 P cos( ) 10 = 10 +1 y A t 1 r cos( ) 20 = 20 + 2 y A t 1 S 2 r cos[ ( ) ] 1 1 1 = 1 − + c r y A t cos[ ( ) ] 2 2 2 = 2 − + c r y A t 2 S 1 2 y = y + y = cos[ ( ) ] 1 1 1 − + c r A t + cos[ ( ) ] 2 2 2 − + c r A t = + + 2 1 2 cos 2 2 2 A A1 A A A I = I 1 + I 2 + 2 I 1 I 2 cos ,( 2 I A ) = [ ( − ) + 2 ]− 2 c r t [ ( ) ] 1 1 − + c r t = ( ) 2 1 2 1 r r c − − − = ( ) 2 2 1 2 1 − − r − r = ( ) 2 2 1 2 1 − − r − r :两列波在 P 点的位相差 r2 − r1 = :波程差 = 2k , k = 0,1,2, A = A1 + A2 最大, 1 2 2 1 2 I = I + I + I I ,干涉加强B A

△0=±(2k+1)π,k=0,1,2…, A=4-A2最小,1=1+12-2√1L2,干涉湘消 如果g,=,△p=-27,-) 干涉加强条件A0-2 元-片)=±2kz 6=5-片=±k,k=0,1,2… 干涉相消条件△p=- 6-)=±2k+10z 6=5-5=2k+号=+22,k=012 4、(1)干涉加强或相消是指合振幅或波的强度最大或最小 而不是合位移最大或最小 (2)位相差恒定要求两个波源在观察时间内持续振动 (3)△p由两部分组成 (4)干涉后,波的能量重新分布 例:A,B两个相干波源,等振幅 x P 20-x 同频率y=100Hz,初相差π 十 相距20m,波速c=200m/s A 20m B 求:A,B连线上因干涉而静止的点 2π 解:△0=0-9-元5-r) =元-2πY(20-x-x)=π-π(20-2x)=(2k+1)r x=10+k,k=0,±1,±2…,±10 x=0,1,…,20m 例:声波干涉仪 E C每移动8cm,声音减弱一次 求:声波的频率 (空气中声速c=340m/s) B D 7A 解:p1=p2 5-5=(2k+12=(k+九(1) 5+2x-5=(k+1+ (2) 2 340 之x=九=,y=C=3 2x2×0.08 =2125E
4 = (2k +1) , k = 0,1,2, A = A1 − A2 最小, 1 2 2 1 2 I = I + I − I I ,干涉相消 如果 1 =2, = ( ) 2 2 1 − r − r 干涉加强条件 = (r r ) 2k 2 − 2 − 1 = = r2 − r1 = k , k = 0,1,2 干涉相消条件 = ( ) (2 1) 2 − r2 − r1 = k + ) 2 1 ( 2 (2 1) = r2 − r1 = k + = k + , k = 0,1,2 4、(1)干涉加强或相消是指合振幅或波的强度最大或最小 而不是合位移最大或最小 (2)位相差恒定要求两个波源在观察时间内持续振动 (3) 由两部分组成 (4)干涉后,波的能量重新分布 例:A,B 两个相干波源,等振幅 x P 20-x 同频率 = 100Hz,初相差 相距 20m,波速 c = 200m/s A 20m B 求:A,B 连线上因干涉而静止的点 解: = ( ) 2 2 1 2 1 − − r − r = (20 ) 2 x x c − − − = − (20 − 2x) =(2k +1) x =10+ k , k = 0,1,2 ,10 x = 0,1, ,20 m 例:声波干涉仪 E C 每移动 8cm,声音减弱一次 x 求:声波的频率 (空气中声速 c = 340m/s ) B D C 1 r 2 r A 解: 1 =2 ) 2 1 ( 2 (2 1) r2 − r1 = k + = k + (1) ) 2 1 r2 + 2x − r1 = (k +1+ (2) c 2x = = , Hz x c 2125 2 0.08 340 2 = = =