西安电子科技大学：《大学物理》课程教学讲义（下）10-4 静电力的功 电势能

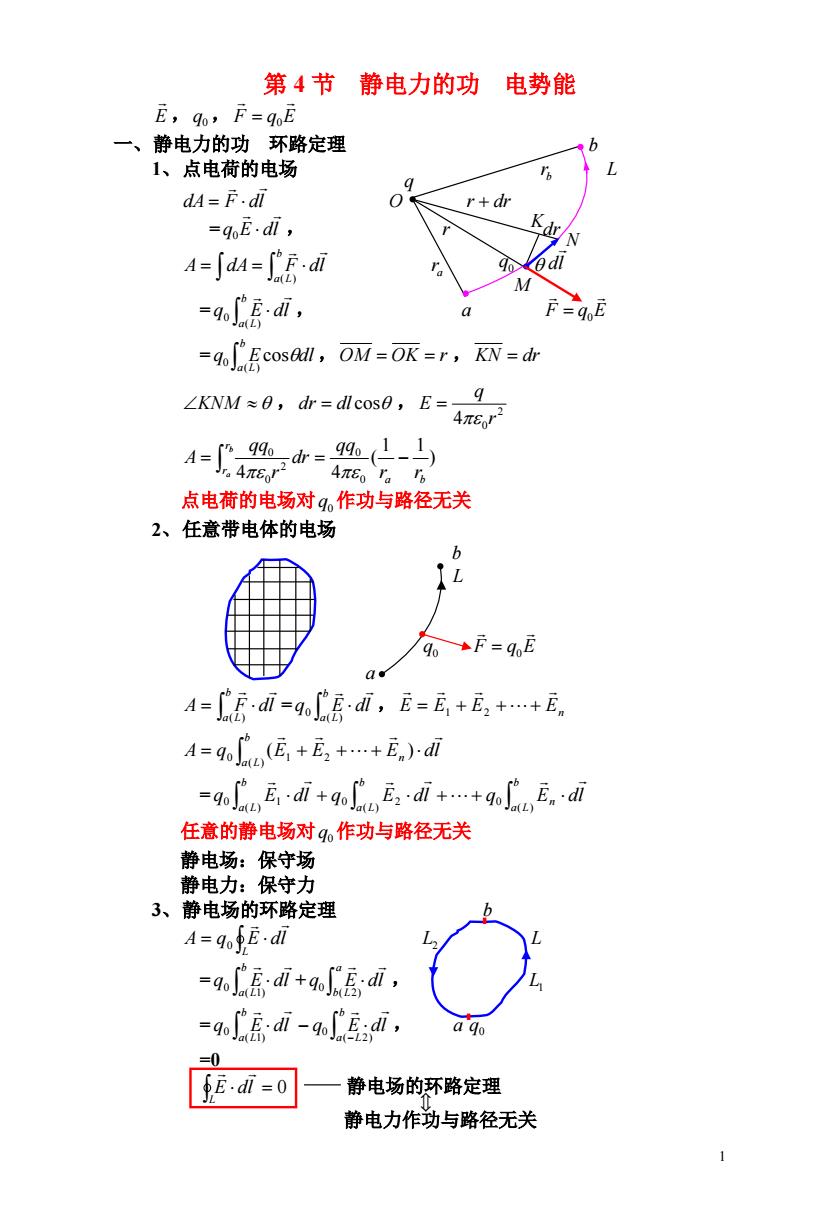
第4节 静电力的功 电势能 E,go,F=qoE 一、静电力的功环路定理 1、点电荷的电场 dA=F.di r+dr =qoE.dl, A=Sdu=SEd 96 d -dod =9E =d.JFcosA,oM=o派=r,不=dt ∠KNM≈0，d=dlcos0,E=,g 4π8I 4器=以 点电荷的电场对q,作功与路径无关 2、任意带电体的电场 90+F=E A=ai=go心Bdi,i=瓦+瓦，++E A=g(E,+E2+…+E)d -gofEd+gof Ed++oEd 任意的静电场对9作功与路径无关 静电场：保守场 静电力：保守力 3、静电场的环路定理 A=qoE.di =gid+小层di, -ao d7-q, a qo =0 fE.di=0 静电场的环路定理 静电力作功与路径无关 1

1 K 第 4 节 静电力的功 电势能 E ， ，  q0 F q E    0 一、静电力的功 环路定理 b 1、点电荷的电场 br L dA F dl     O r  dr = q E dl ，    0 r dr      b a L A dA F dl ( )  ar  = ，   b a L q E dl ( ) 0   a F q E    0 =  ， ， b a L q E dl ( ) 0 cos OM  OK  r KN  dr KNM  ，dr  dl cos ， 2 4 0r q E   ) 1 1 ( 4 4 0 0 2 0 0 a b r r r r qq dr r qq A b a       点电荷的电场对q0 作功与路径无关 2、任意带电体的电场 b L q0 F q E    0 a    = ， b a L A F dl ( )    b a L q E dl ( ) 0   E E E En       1  2         b a L n A q E E E dl ( ) 0 1 2 ( )      =          b a L n b a L b a L q E dl q E dl q E dl ( ) 0 ( ) 0 2 ( ) 0 1        任意的静电场对q0 作功与路径无关 静电场：保守场 静电力：保守力 3、静电场的环路定理 b    L A q E dl   0 L2 L = + ，   b a L q E dl ( 1) 0     a b L q E dl ( 2) 0   L1 = ，   b a L q E dl ( 1) 0       b a L q E dl ( 2) 0   a q0 =0    0 静电场的环路定理 L E dl   静电力作功与路径无关 q0 N M dl q 

例：静电场的电力线不能是闭合曲线 证：反证法，设静电场的某条电力线 是闭合曲线 5E·di=∮E cos@d>0 d 静电场的环路定理只适用于静电场 二、电势能 R:参考点 oE-d 定义：电势能所，=9Ed 注意： （1)W,与A的区别 (2)A与△W的关系 A-qoEdT=qoEdi+qoEdi =gE.di-9。E.di=形。-。=-W。-m,) W。-Wp=△W:电势能增量，A=-△W A>0,△W0,W↑ (3)参考点：me=gE.d=0 理论上：“∞”，W,=Ed 工程上：“大地” R:参考点，那=gEi,m,≠Wg 电势能的数值只具有相对意义 9。在静电场中任意两点上电势能的差值 与参考点的选择无关 第5节 电势和电势差 一、定义W。=qEdi,W,cqo,W,1g。=∫Ed 电势：Up=w,1go=∫E 注意：(1)标量，SI:J/C=V(伏) (2)Wp=qoUp (3)Up-Uo=Ue:电压，SI:V Uo=Up-U。=∫E.di-E.di =∫Eai+Eai-Ea Uro-E.di 2

2 例：静电场的电力线不能是闭合曲线 证：反证法，设静电场的某条电力线 是闭合曲线   cos  0 L L E dl E dl   dl E  静电场的环路定理只适用于静电场 二、电势能 R ：参考点 E    R P q E dl   0 R R 定义：电势能    R P P W q E dl   0 注意： （1） 与 的区别 WP A P q0 （2） A与W 的关系 = +    Q P A q E dl   0   R P q E dl   0   Q R q E dl   0 = =   R P q E dl   0    R Q q E dl   0 ( ) WP WQ   WQ WP WQ WP  W ：电势能增量， A  W A  0 ，W  0 ，W ； A  0 ，W  0 ，W  （3）参考点：  0   0  R R R W q E dl   理论上：“”，    P P W q E dl   0 工程上：“大地” R：参考点，  ，     R P P W q E dl   0 WP WP   电势能的数值只具有相对意义 q0 在静电场中任意两点上电势能的差值 与参考点的选择无关 第 5 节 电势和电势差 一、定义    ， ， R P P W q E dl   0 WP  q0    R P P W q E dl   0 / 电势：     R P P P U W q E dl   0 / 注意：（1）标量，SI：J/C=V（伏） （2）WP  q0UP （3）UP UQ  UPQ ：电压，SI：V UPQ  UP UQ =   R P E dl      R Q E dl   = + =   R P E dl     Q R E dl     Q P E dl      Q P PQ U E dl   Q

(4)6:P→0，A=go∫E.di=qUe (5)电势与参考点的选择有关 电压与参考点的选择无关 U=Edi=0 参考点=电势能零点=电势零点 二、电势的计算 0 1、点电荷 Up=∫E.i o为参考点 U,=SE-di -Ecosell,cos0=1,dl=dr,E= -品 4π6oJ R:参考点 U,=E.di - 2d, P =9-马. q 4π8ra 2、点电荷系 o为参考点 U,-SE.di E=E+E2+…+E Up=∫(E+E2++E,)d 92 =E-di+E·di+…+E.di =9+,4-+…+,9 4π814π6o5 ATEoFn Up=U,+U2+…+Un 电势迭加原理 3、连续电荷分布的电势 d0= dq 4πE,' dv dq 计算电势的两种方法： 3

3 （4）q0 ： P  Q ， =    Q P A q E dl   0 UPQ q0 （5）电势与参考点的选择有关 电压与参考点的选择无关    0  R R R U E dl   参考点=电势能零点=电势零点 二、电势的计算  1、点电荷 E     R P P U E dl   dl 为参考点 r P    P P U E dl   q =  ， ， ，  P Ecosdl cos 1 dl  dr 2 4 0r q E   = dr = r q r 2 0 4 r q 4 0  R ：参考点    R P P U E dl   R = dr ， r a q r 2 4 0  P a = ) 。 1 1 ( 4 0 r a q   q 2、点电荷系 P 为参考点    P P U E dl   1r 2r nr E E E En       1  2   q1       P P n U E E E dl      ( ) 1 2 n q = +   P E dl   1        P E dl 2   P n E dl   = + 0 1 1 4 r q   0 2 2 4 r q  n n r q 4 0  UP  U1 U2 Un 电势迭加原理 3、连续电荷分布的电势 P r dq dU 4 0   dU     r dq U dU 0 4 计算电势的两种方法： r r q2 dq

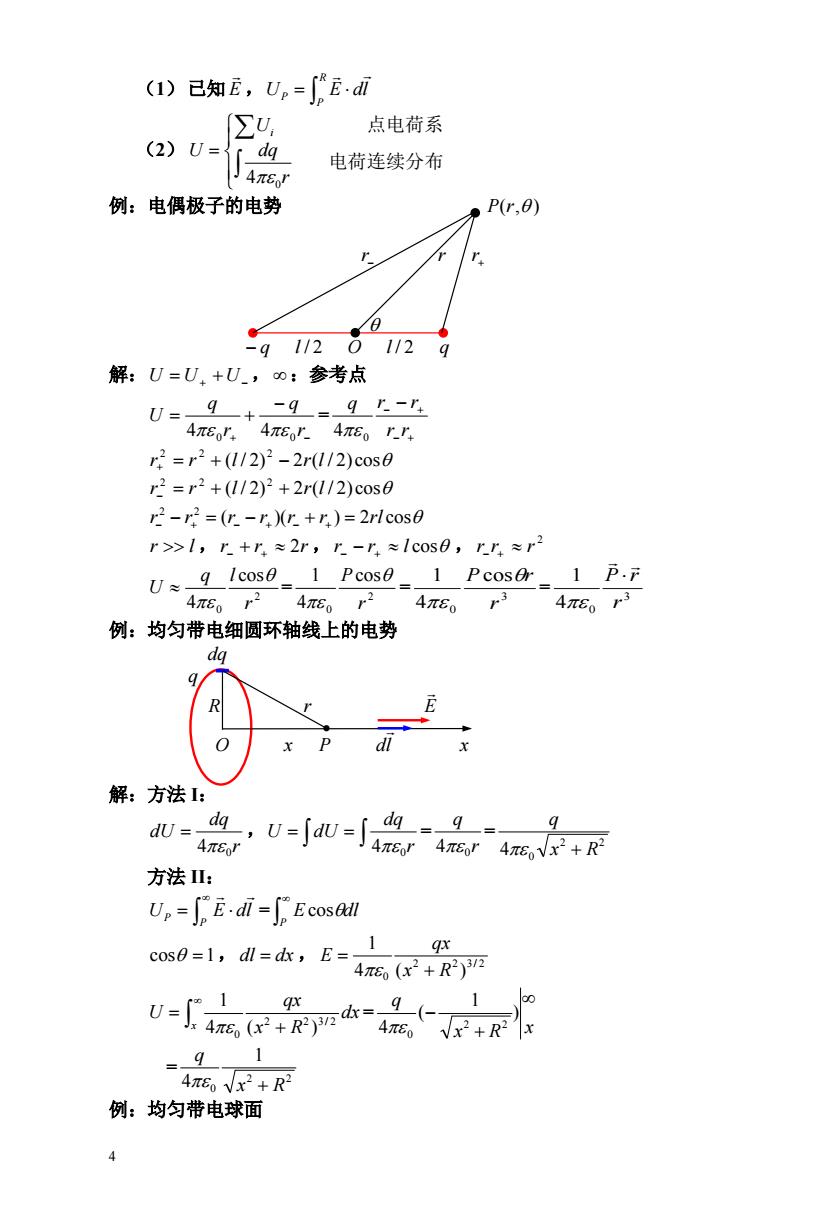
(1)已知E,U,=∫E.di 点电荷系 (2)U= 电荷连续分布 J4π6r 例：电偶极子的电势 P(r,8) -q11201129 解：U=U,+U_,o:参考点 U=,9+-9=9上-y 4πEo上，4πEo上4πE0rr =r2+(1/2)2-2r(I12)cos0 r2=r2+(I/2)2+2rI/2)cos0 r2-r2=(r-r,)(r+r.)=2rlcose r>1,r+r≈2r,r-r≈1c0s0，rr≈r2 U≈，91cos9-1Pcos8=1 Pcoser.1p.F 4π6。r2 4πE0r2 4πE0r3 4π60r3 例：均匀带电细圆环轴线上的电势 dg 解：方法1： 0高，u=w=岛品+R 9 4π6r 方法： U=E.di=Ecosedl coso=1,dl=dx,E=-19x 46(x2+R2)3n =91 4π6Vx2+R 例：均匀带电球面 4

4 （1）已知 E ，    R P P U E dl   （2）         电荷连续分布 点电荷系 r dq U U i 4 0  例：电偶极子的电势 P(r, ) r r r   q l / 2 O l / 2 q 解：U  U U ，：参考点 =      r q r q U 4 0 4 0        r r q r r 4 0  ( / 2) 2 ( / 2) cos 2 2 2 r  r  l  r l  ( / 2) 2 ( / 2) cos 2 2 2 r  r  l  r l  ( )( ) 2 cos 2 2 r  r  r  r r  r  rl       r  l ，r  r  2r ，r  r  l cos ， 2 r r  r   = = = 2 0 cos 4 r q l U    2 0 cos 4 1 r P   3 0 cos 4 1 r P r  3 4 0 1 r P r     例：均匀带电细圆环轴线上的电势 dq q R r E  解：方法 I： ， = = r dq dU 4 0       r dq U dU 0 4 r q 4 0  2 2 4 0 x R q   方法 II： =    P P U E dl    P Ecosdl cos 1，dl  dx ， 2 2 3 / 2 0 4 ( ) 1 x R qx E    =    x dx x R qx U 2 2 3 / 2 0 4 ( ) 1  x R x q    ) 1 ( 4 2 2  0  = 2 2 0 1 4 x R q   例：均匀带电球面 O x P dl x

●■”■■■■■”● 0 r P dl 00 0 rR 4πer2 (1)r>R,U,=Edi=Ecoso-dl -品 4π8o' (2)rR 4πEr 电势是连续的 R 例：无限长均匀带电直线 : di E 解E2,,-Ed-5o0 5

5 Q O r P dl   R 解：         r R r Q r R E 2 4 0 0  （1）r  R， =    P P U E dl     P Ecos dl =   r dr r Q 2 4 0  r Q 4 0  （2）r  R Q O r P M dl   = = +    P P U E dl     P Ecos dl   M P Ecos dl   M Ecos dl = = ，  R dr r Q 2 4 0  R Q 4 0  U        r R r Q r R R Q U 0 0 4 4   电势是连续的 R r 例：无限长均匀带电直线  dl r P E  解： ， = r E 2 0       P P U E dl     P Ecos dl =  = ，无意义  r dr r 2 0   r r  ln 2 0   E  E  R Q 4 0   R