西安电子科技大学：《大学物理》课程教学讲义（下）10-3 场强计算与高斯定理习题课

场强计算与高斯定理习题课 例：无限长均匀带电直线E= 2π6oY 解： d、 n dl'=dl O dl Φ=fEa西 -EcosaiS, -Ecoseds, +EcosiS, +Ecoseds, =E=E-2m1=八，E= 60 2π6r 问题1、高斯面只包围了部分电荷，求出的场强是这一 部分电荷的场强还是整根均匀带电直线的场强？ 问题2、对于一段有限长均匀带电直线段，能否用该方法 求其场强？ Φ=fE5= 轴对称电场 1

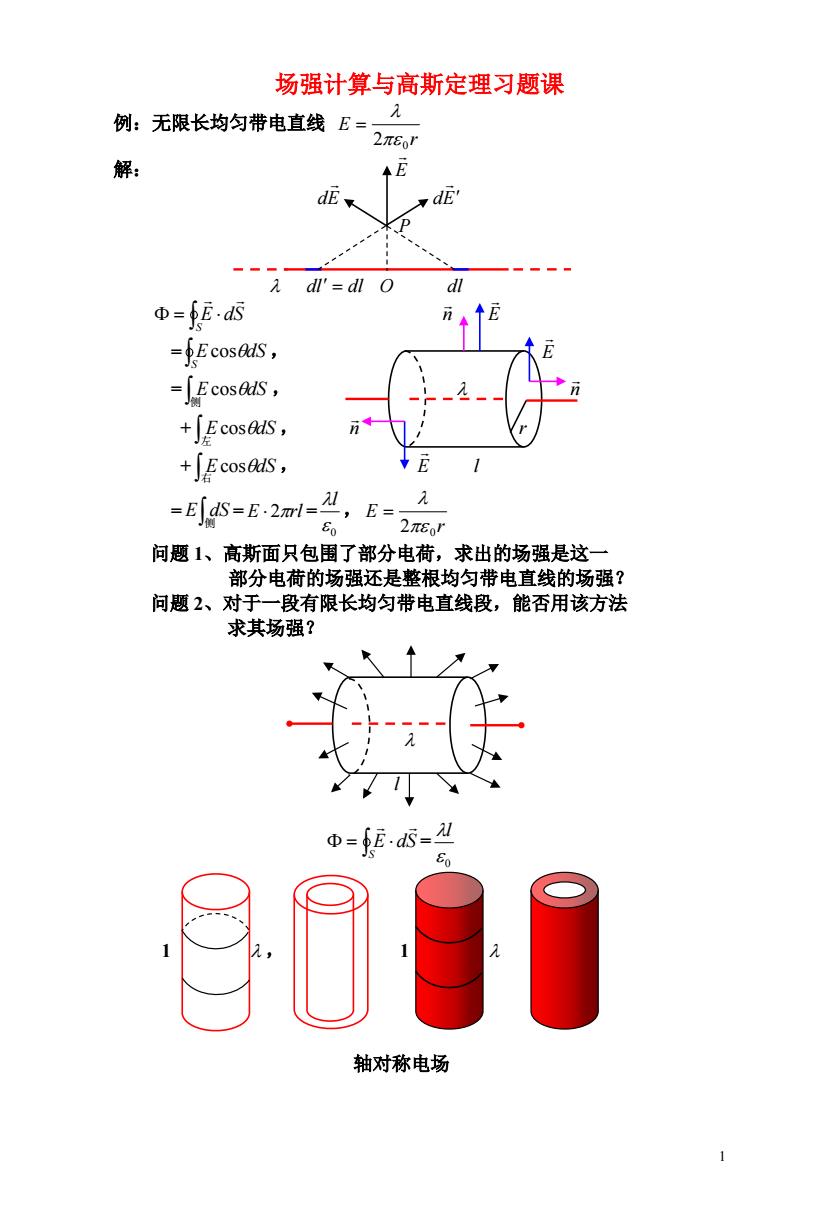
1 场强计算与高斯定理习题课 例：无限长均匀带电直线 r E 2 0    解： E  dE  dE   dl  dl O dl     S E dS   n  E  = ， S EcosdS E  = ， 侧 E cosdS  n  + ， 左 EcosdS n  r + ， 右 EcosdS E  l =  = = ， 侧 E dS E  2rl 0  l r E 2 0    问题 1、高斯面只包围了部分电荷，求出的场强是这一 部分电荷的场强还是整根均匀带电直线的场强？ 问题 2、对于一段有限长均匀带电直线段，能否用该方法 求其场强？  l =     S E dS   0  l 1  ， 1  轴对称电场 P

例：无限大均匀带电平面E三 解： E Φ=5Ea E -fEcosais, -Fcosads, E S E +Ecosais, h +Ecoseds -0+ES+ES=2ES=05 ，E= 0 260 ↑E 280 0 x 280 例： g>0 E E E E E E I, Ⅲ 求：E 解：E=E+E I、E=0 II、E=E++E= +0=0 26026060 I、E=0 2

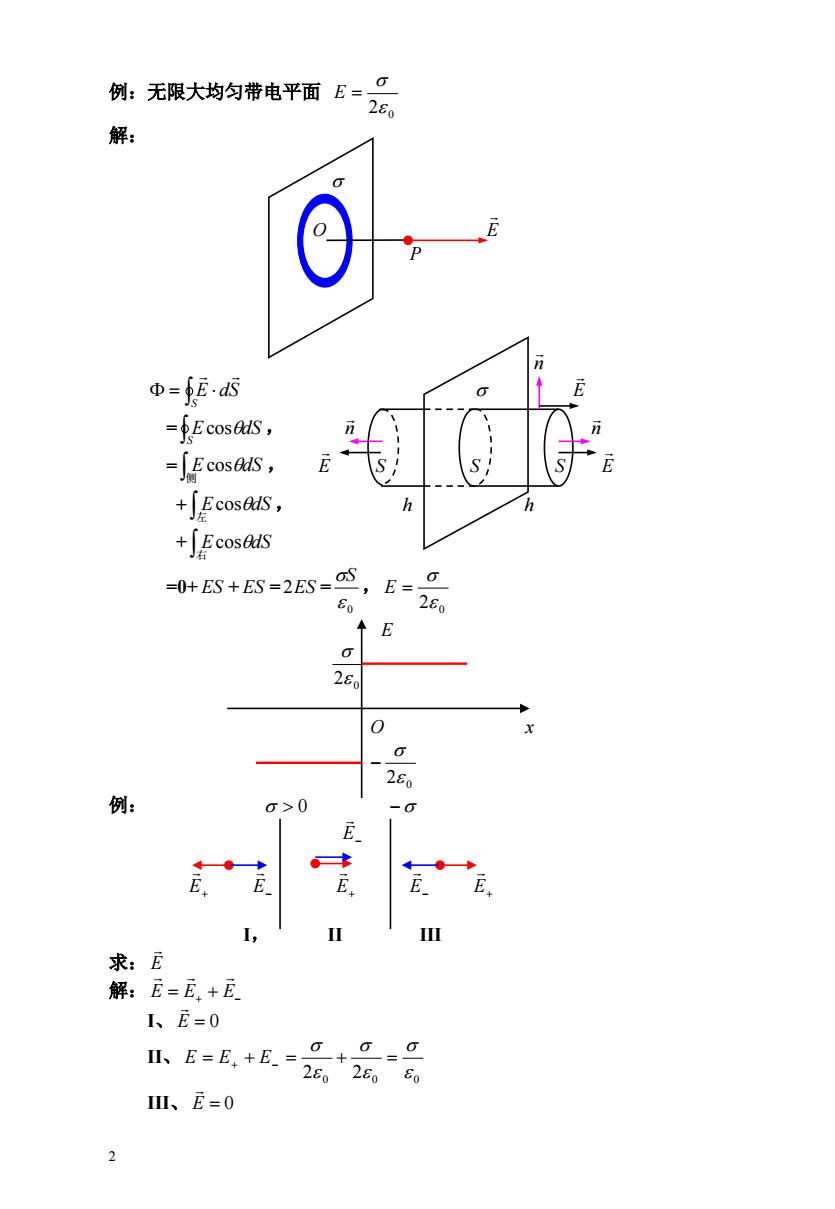
2 例：无限大均匀带电平面 2 0   E  解：  O E  P n      S E dS    E  = ， S EcosdS n  n  = ， 侧 E cosdS E  S S S E  + ， 左 EcosdS h h + 右 EcosdS =0+ ES + ES = 2ES = ，0  S 2 0   E  E 2 0   O x 0 2   例：   0  E  E  E  E  E  E  I， II III 求： E  解： E  E  E    I、 E  0  II、 2 0 2 0 0       E  E  E    III、 E  0 

σ>0 0>0 关于高斯定理： 1、Φ=E5-∑9 0内 Φ仅与∑9，有关，E与所有电荷及其分布有关 2如果Φ已知，∑9=6柜-5=0 但仅由Φ和高斯定理不能完全确定高斯面内电荷分布 如Φ=0，∑9，=0 判断下面几种说法的正确性： (1)如果高斯面上E处处为零，则高斯面内必无电荷 Φ=fE·=0,∑9，=0 (2)如果高斯面内无电荷，则高斯面上E处处为零 ∑9，=0，Φ=Es=∑9，=0，XE=0 (3)如果高斯面上E处处不为零，则高斯面内必有电荷 (4)如果高斯面内有电荷，则高斯面上E处处不为零 由高斯定理求电场强度的思路： 电荷分布的对称性一电场分布的对称性 一适当的选取高斯面(ELn,E∥n) 一将E从积分号内提出，化积分方程为代数方程求E 3

3   0    0 E  O x 关于高斯定理： 1、      内 i S E dS q 0 1     仅与 有关， 与所有电荷及其分布有关 内 i q E  2、如果 已知，   0     0 S i q E dS   内 但仅由 和高斯定理不能完全确定高斯面内电荷分布 如 =0，  0 内 i q 判断下面几种说法的正确性： （1）如果高斯面上 E 处处为零，则高斯面内必无电荷       0 ， S E dS     0 内 i q Q  Q S （2）如果高斯面内无电荷，则高斯面上 E 处处为零    0 ， =0， 内 i q       内 i S E dS q 0 1     E  0  q S （3）如果高斯面上 E 处处不为零，则高斯面内必有电荷  （4）如果高斯面内有电荷，则高斯面上 E 处处不为零  由高斯定理求电场强度的思路： 电荷分布的对称性电场分布的对称性 适当的选取高斯面（ E n ， ）   E n   // 将 E 从积分号内提出，化积分方程为代数方程求 E

补偿法求电场强度 例：求圆孔轴线上的E x P 解：E=+ 2e2e√x2+R2 28Vx2+R2 例：求轴线上的E R R R 解：E=01- 260 + Vx2+R2 -60 280 Vx2+R2 例：求小球腔中的电场 E=POP+POP=P (OP-OP)-P 0O 3638 380 38 小球腔内是均匀电场 E=P00,方向0可 380 4

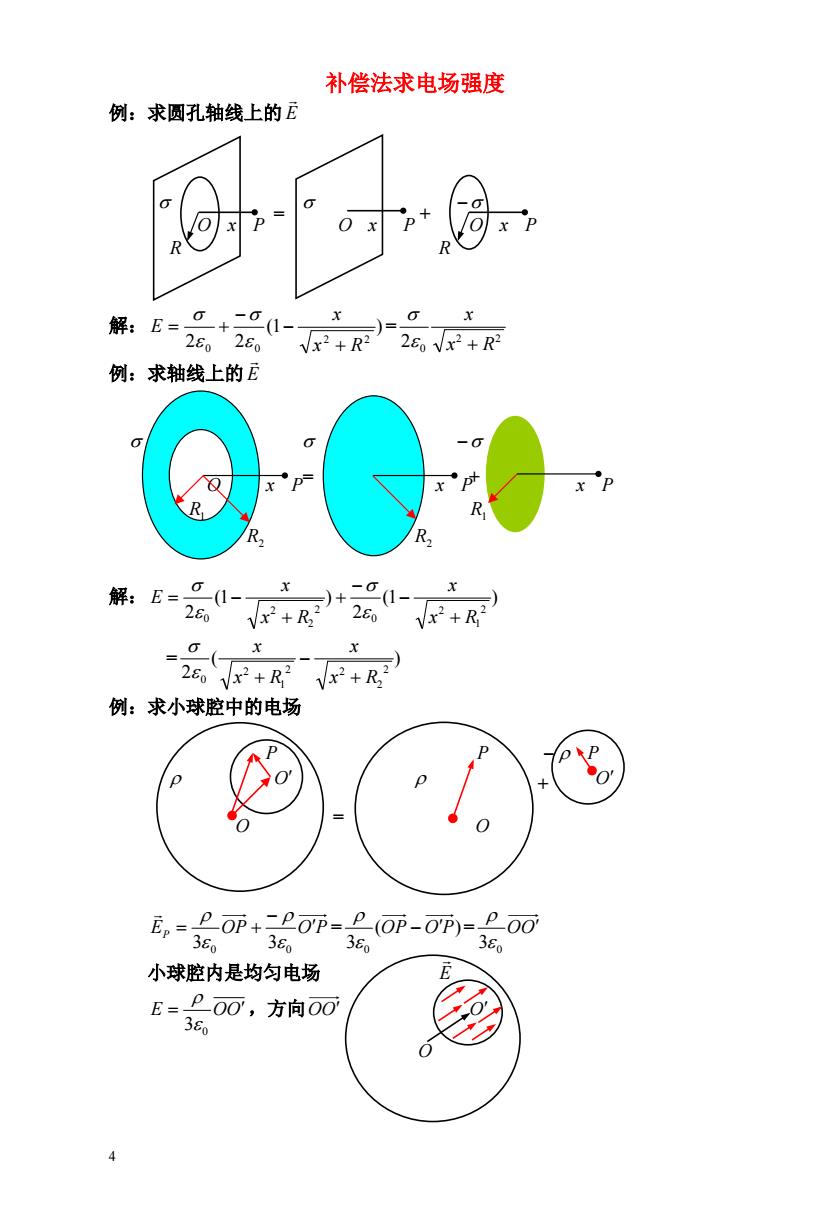
4 补偿法求电场强度 例：求圆孔轴线上的 E     O x P O x P O x P R R 解： (1 ) = 2 2 2 2 0 0 x R x E          2 2 2 0 x R x    例：求轴线上的 E     O x P x P x P R1 R1 R2 R2 解： (1 ) 2 (1 ) 2 2 1 2 0 2 2 2 0 x R x x R x E            = ( ) 2 2 2 2 2 1 2 0 x R x x R x      例：求小球腔中的电场 P P   P  O  O O O EP OP OP = =    0 0 3 3     ( ) 3 0 OP  OP   OO 3 0   小球腔内是均匀电场 E  E  OO，方向 3 0   OO O O = + = + + =

例：求通过圆锥侧面的电通量 解：Φ=后a Φ=fE·a因 9 =可Es+jE西= Eo =县-0 R Φ底=∫E=SEcos0.ds n E h/2 西=2mth,E-4r十h12'cos0 Vr2+(h12) -+严是品42 rdr =9-9 h h D则=9-we2运+4R+h/2 例：无限长均匀带电半圆柱面 沿轴向单位长度带电入 求：轴线上E 解：o= P 2πER 2'=adl=2dl πR dE 1 dl 2πE,RπR 2r's Rdl dE,=-dE cos0 dE,=-dEsine dl Rd0 E,=∫dE,=∫-dEcose0 dE, -d8 Rde cos0, 2π28R2 dE -dE =0 E,=∫dE,=∫-dEsin8 :Rdosino- π 2π26R 2π26R 0π28R E=Ei+E,j=--Aj π28R 5

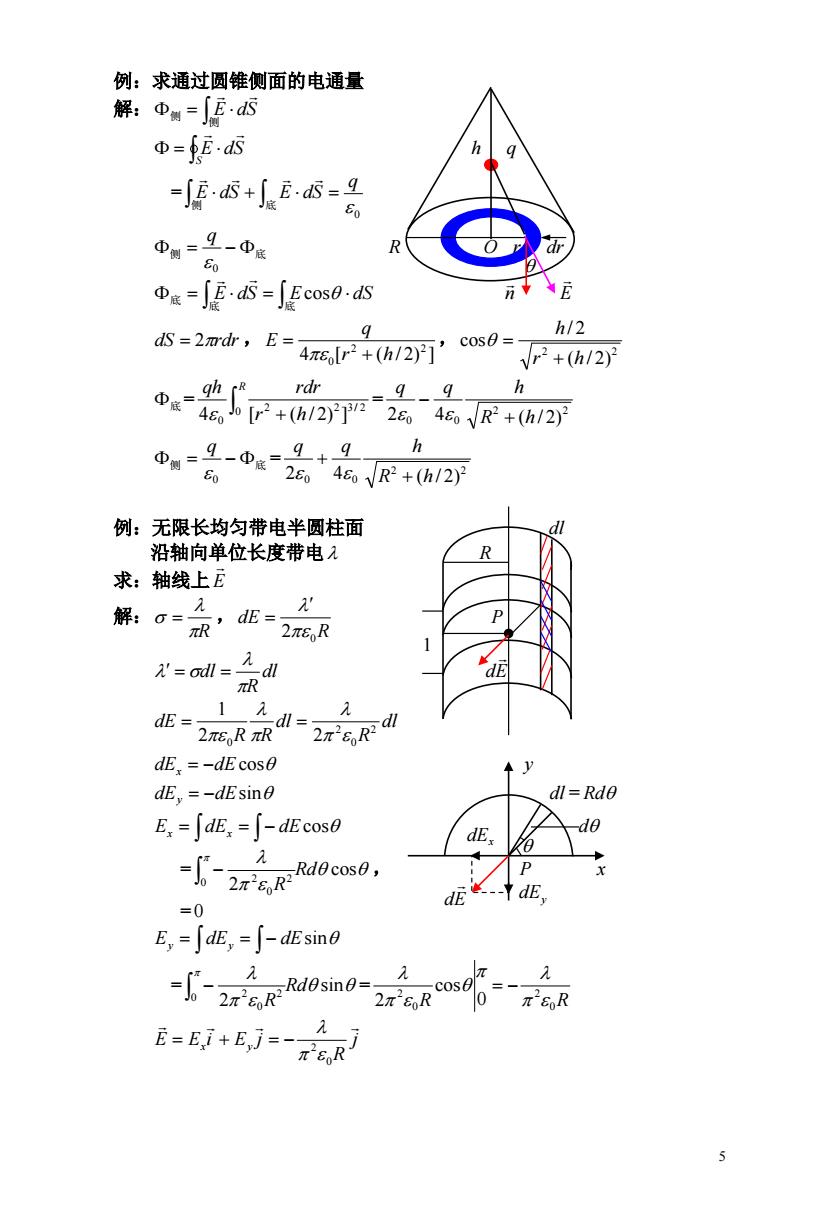
5 例：求通过圆锥侧面的电通量 解：     侧 侧 E dS       S E dS   h q =       侧 底 0  q E dS E dS     侧   底 0  q R O r dr        底 底 底 E dS Ecos dS   n  E  dS  2rdr ， ， 4 [ ( / 2) ] 2 2 0 r h q E    2 2 ( / 2) / 2 cos r h h    底 = =   R r h qh rdr 0 2 2 3 / 2 0 4 [ ( / 2) ] 2 2 2 0 4 0 R (h / 2) q q h     侧   底 = 0  q 2 2 2 0 4 0 R (h / 2) q q h     例：无限长均匀带电半圆柱面 dl 沿轴向单位长度带电 R 求：轴线上 E  解： ， R    R dE 2 0    P dl R dl       dE  dl R dl R R dE 2 0 2 2 0 2 1         dE dEcos x   y dEy  dEsin dl = Rd   Ex  dEx   dEcos d =   ，     cos 0 2 2 0 2 Rd R   P x =0   Ey  dEy   dEsin =   =     sin 0 2 2 0 2 Rd R   R 0R 2 0 2 0 cos 2           j R E E i E j x y     0 2          1 dEy dEx dE 