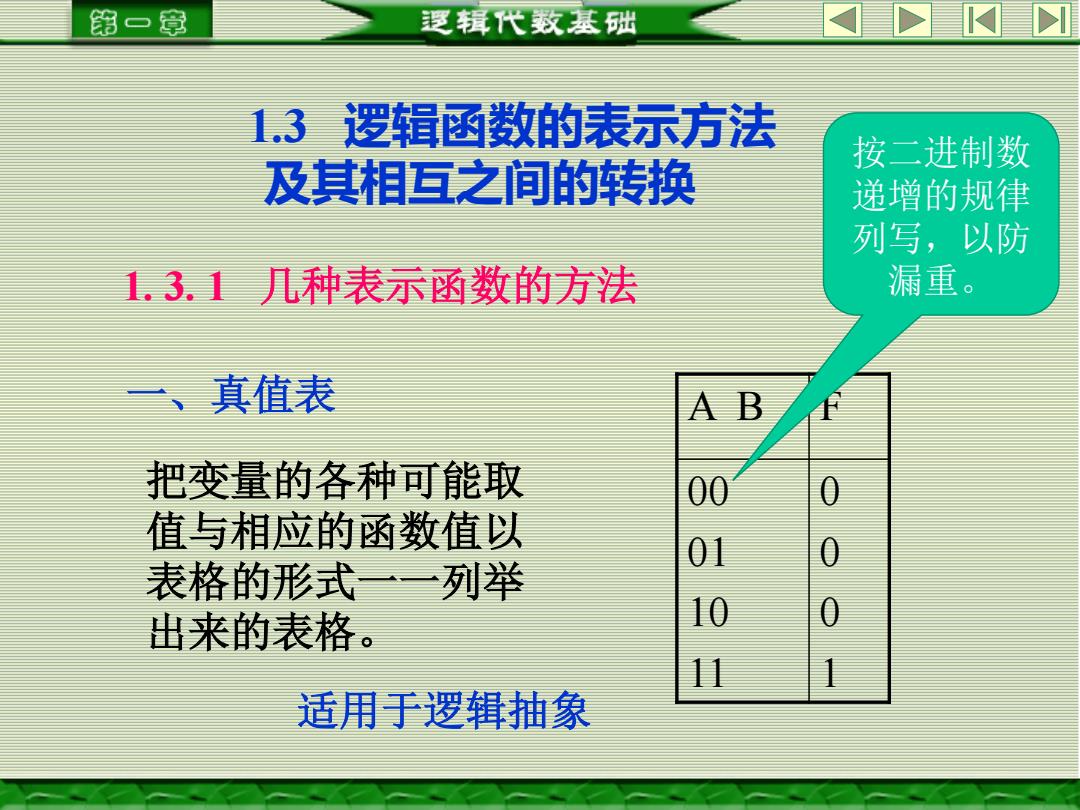
第一章 逻辑代数基础 1.3逻辑函数的表示方法 按二进制数 及其相互之间的转换 递增的规律 列写,以防 L.3.1几种表示函数的方法 漏重。 一、真值表 把变量的各种可能取 0 值与相应的函数值以 表格的形式一一列举 出来的表格。 适用于逻辑抽象
1.3 逻辑函数的表示方法 及其相互之间的转换 1. 3. 1 几种表示函数的方法 一、真值表 把变量的各种可能取 值与相应的函数值以 表格的形式一一列举 出来的表格。 A B F 00 01 10 11 0 0 0 1 适用于逻辑抽象 按二进制数 递增的规律 列写,以防 漏重
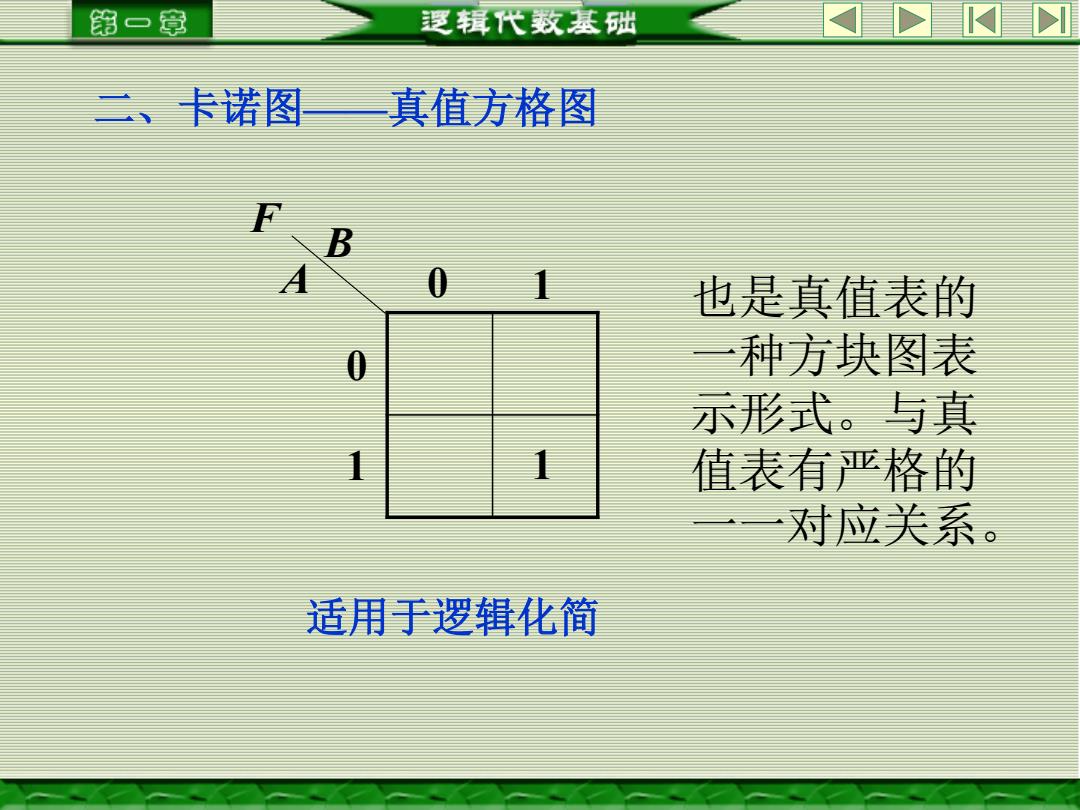
第一章 逻辑代数基础 二、卡诺图 真值方格图 f、B 01 也是真值表的 0 种方块图表 示形式。与真 值表有严格的 对应关系。 适用于逻辑化简
二、卡诺图——真值方格图 A B 0 1 0 1 F 1 适用于逻辑化简 也是真值表的 一种方块图表 示形式。与真 值表有严格的 一一对应关系

第一章 逻辑代数基础 三、逻辑表达式 用与、或、非等运算表示函数中各个变量之 间逻辑关系的代数式子,称为逻辑表达式。 Y=AB+AC+BC 四、逻辑图 用基本和常用的逻辑符号表示函数表达式中各 个变量之间的运算关系,便得到了函数的逻辑 图。 逻辑图最接近实际电路图
三、逻辑表达式 用与、或、非等运算表示函数中各个变量之 间逻辑关系的代数式子,称为逻辑表达式。 Y AB AC BC = + + 四、逻辑图 用基本和常用的逻辑符号表示函数表达式中各 个变量之间的运算关系,便得到了函数的逻辑 图。 逻辑图最接近实际电路图
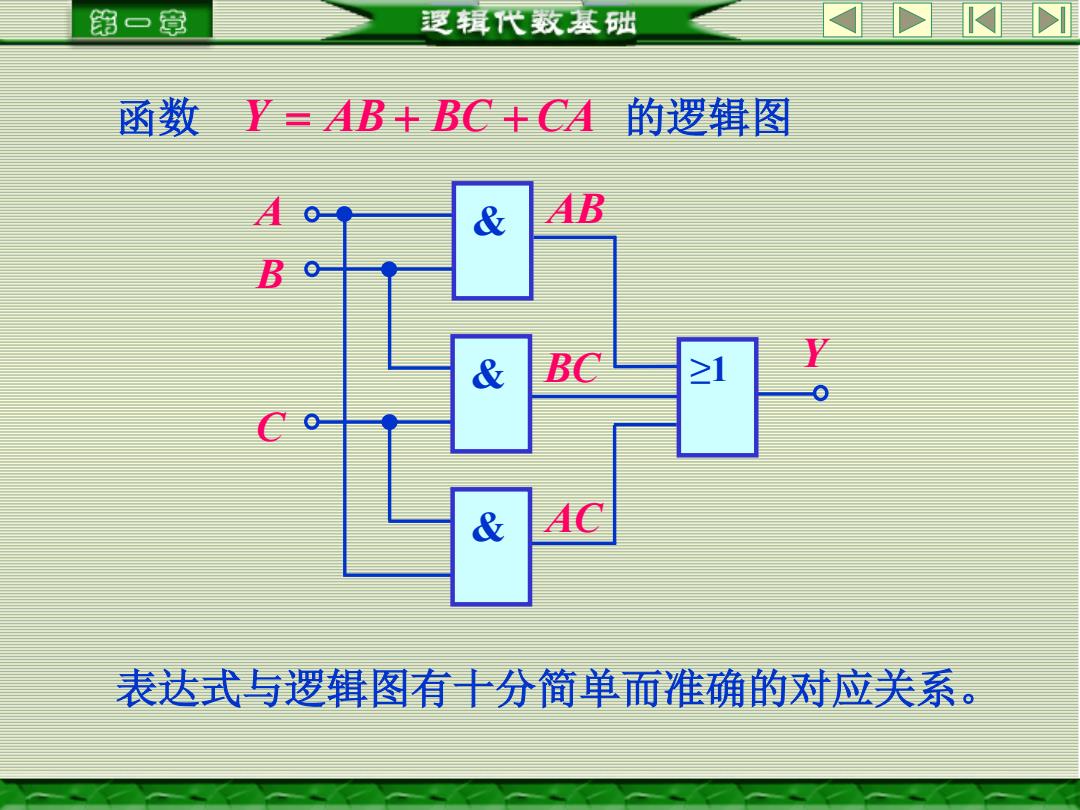
第一章 逻辑代数基础 函数Y=AB+BC+CA的逻辑图 & AB B & BC ≥1 & AC 表达式与逻辑图有十分简单而准确的对应关系
函数 Y = AB + BC + CA 的逻辑图 A B Y C & & & ABBCAC ≥1 表达式与逻辑图有十分简单而准确的对应关系
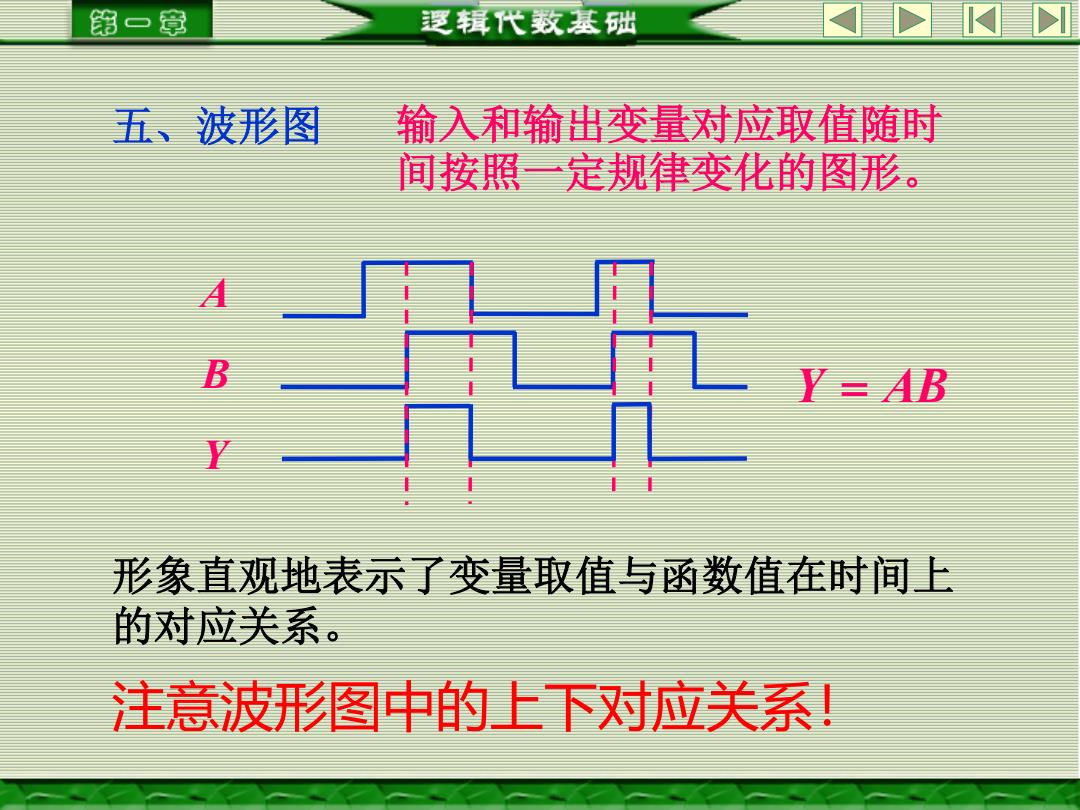
第一章 逻辑代数基础 五、波形图 输入和输出变量对应取值随时 间按照一定规律变化的图形。 B Y=AB 形象直观地表示了变量取值与函数值在时间上 的对应关系 。 注意波形图中的上下对应关系
五、波形图 输入和输出变量对应取值随时 间按照一定规律变化的图形。 Y = AB A B Y 形象直观地表示了变量取值与函数值在时间上 的对应关系。 注意波形图中的上下对应关系!
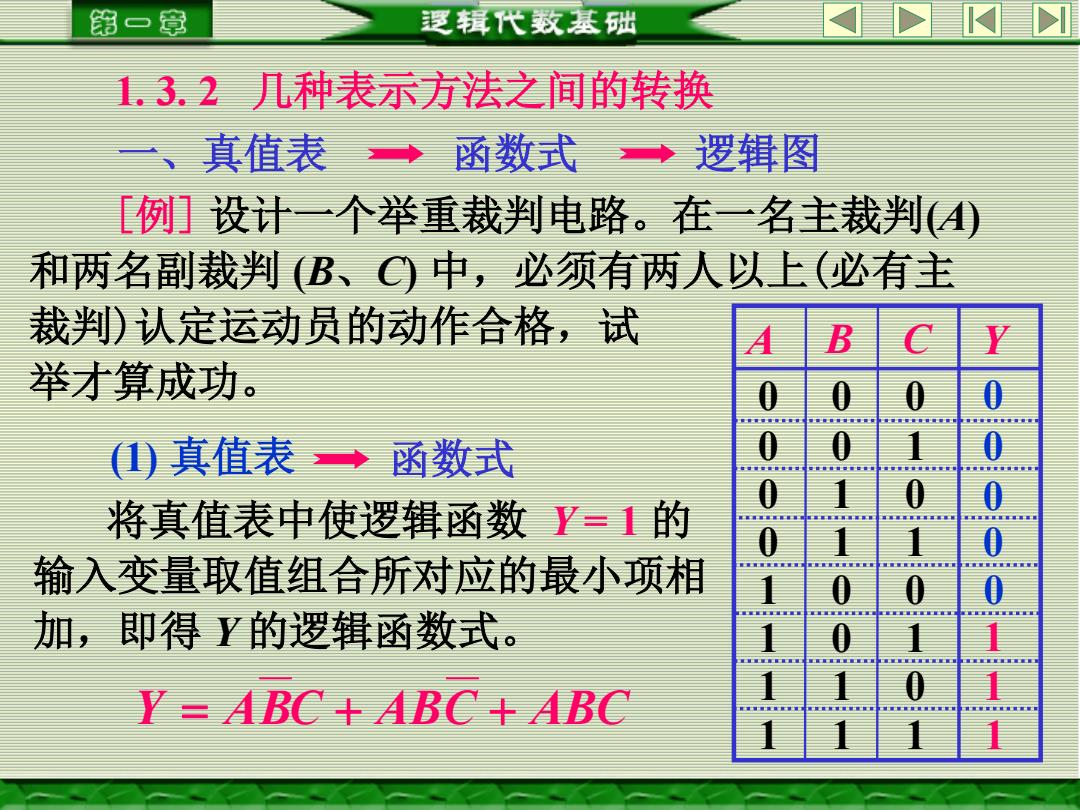
第一章 逻辑代数基础 1.3.2几种表示方法之间的转换 一、真值表◆ 函数式→逻辑图 [例们设计一个举重裁判电路。在一名主裁判( 和两名副裁判(B、○中,必须有两人以上(必有主 裁判)认定运动员的动作合格,试 B 举才算成功。 ()真值表→函数式 将真值表中使逻辑函数Y=1的 输入变量取值组合所对应的最小项相 复重银重复复 置 重 推推 量推推 加,即得Y的逻辑函数式。 推 报 指重重 Y=ABC+ABC+ABC
1. 3. 2 几种表示方法之间的转换 一、真值表 函数式 逻辑图 [例] 设计一个举重裁判电路。在一名主裁判(A) 和两名副裁判 (B、C) 中,必须有两人以上(必有主 裁判)认定运动员的动作合格,试 举才算成功。 (1) 真值表 函数式 Y = ABC + ABC + ABC 将真值表中使逻辑函数 Y = 1 的 输入变量取值组合所对应的最小项相 加,即得 Y 的逻辑函数式。 A B C Y 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0 0 0 1 1 1
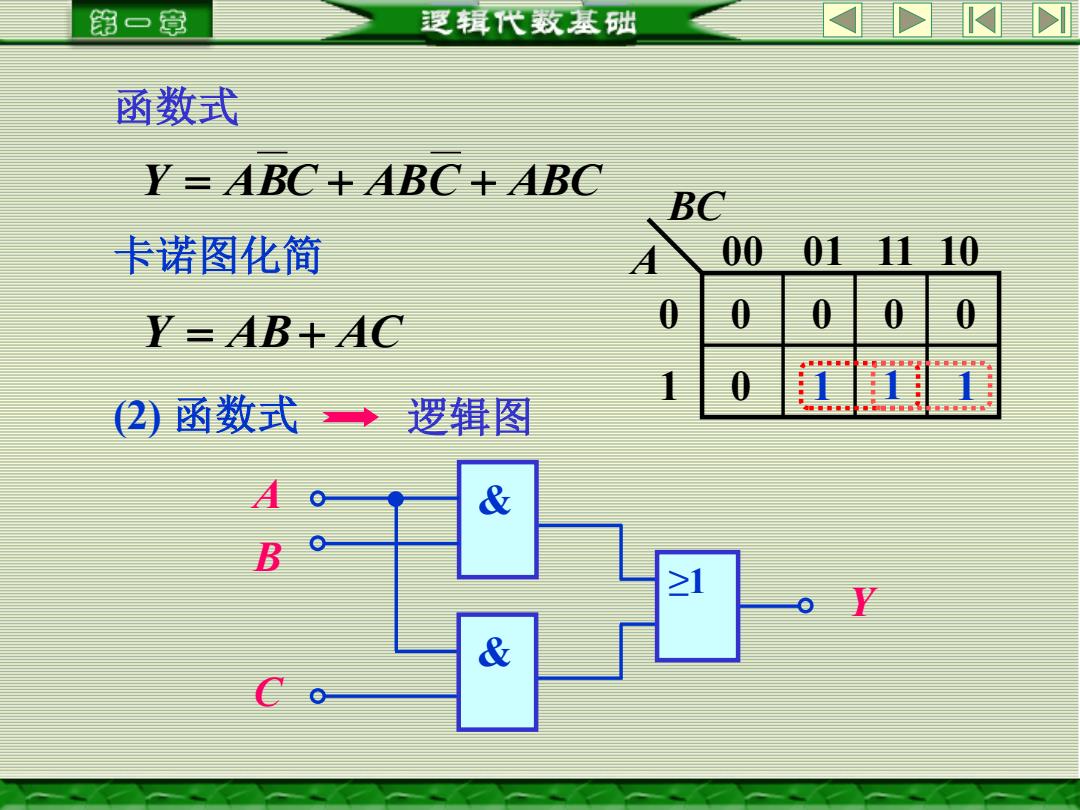
第一章 逻辑代数基础 函数式 Y=ABC+ABC+ABC BC 卡诺图化简 00011110 Y=AB+AC 0 0 (2)函数式→逻辑图 & B ≥1 o y &
函数式 Y = ABC + ABC + ABC 卡诺图化简 A BC 0 1 00 01 11 10 1 1 0 1 0 0 0 0 Y = AB+ AC (2) 函数式 逻辑图 A B Y & C & ≥1
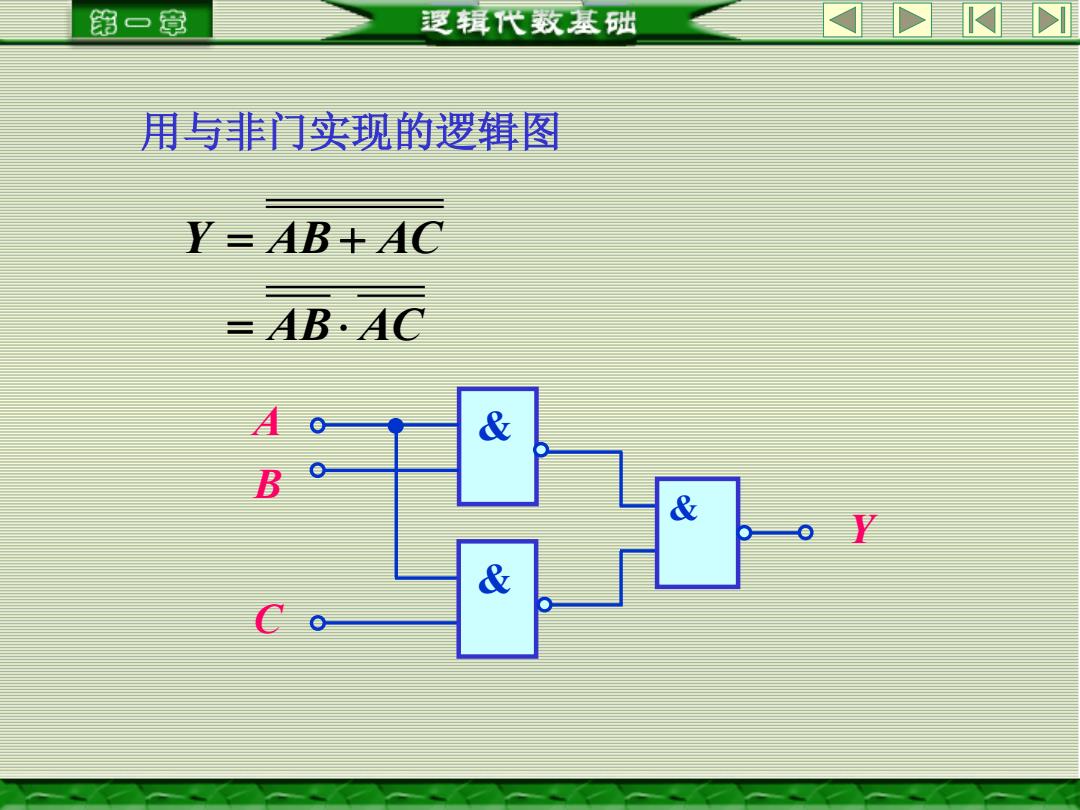
第一章 辑代数基础 用与非门实现的逻辑图 Y=AB+AC AB.AC & B & o Y &
用与非门实现的逻辑图 Y AB AC AB AC = + = A B Y & C & &

第一章 逻辑代数基础 二、逻辑图 →真值表 & A·AB & AB & & Y=A·AB.B·AB B·AB B =A·AB1B.AB =A(4+B)+B(4+B B 0 AB+AB =A⊕B 康泰泰单泰泰泰象装司 ■想形板参日都
二、逻辑图 真值表 Y = A AB B AB = A AB + B AB = A(A+ B) + B(A+ B) = AB + AB = A B 0 1 1 0 A B Y 0 0 0 1 1 0 1 1 AB A AB B AB B A Y & & & &